Интервальные оценки

11.1. Доверительные интервалы и доверительная вероятность.

Доверительные интервалы для параметров нормально распреде­ленной

генеральной совокупности.

При статистической обработке результатов наблюдений следует не только найти оценку 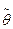неизвестного параметра θ, но и охарактеризовать точность этой оценки. С этой целью вводится понятие доверительного интервала.

Доверительным интервалом для параметра θ называется интервал (θ₁, θ₂), содержащий (накрывающий) истинное значение θ с заданной вероятностью р = 1 - α, т.е. Р [ θ₁ < θ < θ₂ ] = 1- α.

Число 1 - α называется доверительной вероятностью, а зна­чение α - уровнем значимости. Статистики θ₁ = θ₁ (x ₁,..., x_n) и θ₂ = θ₂ (x ₁,..., x_n), определяемые по выборке x ₁,..., x_n из генераль­ной совокупности с неизвестным параметром θ, называются со­ответственно нижней и верхней границами доверительного ин­тервала.

Условие Р [ θ₁ < θ < θ₂ ] = 1- α означает, что в большой серии независимых экспериментов, в каждом из которых получена вы­борка объема n, в среднем (1 - α)·100% из общего числа построенных доверительных интервалов содержат истинное значение параметра θ.

Длина доверительного интервала, характеризующая точ­ность интервального оценивания, зависит от объема выборки n и доверительной вероятности 1 - α: при увеличении объема выборки длина доверительного интервала уменьшается, а с приближе­нием доверительной вероятности к единице - увеличивается. Вы­бор доверительной вероятности определяется конкретными усло­виями. Обычно используются значения 1 - α, равные 0,90; 0,95; 0,99.

При решении некоторых задач применяются односторонние доверительные интервалы, границы которых определяют из усло­вий: Р [ θ < θ₂ ] = 1- α или Р [ θ₁ < θ ] = 1- α.

В этом случае интервалы называются соответственно левосторонними и правосторонними доверительными интервалами.

Чтобы найти доверительный интервал для параметра θ, на­до знать закон распределения статистики 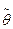= 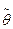(х₁,...,х_п), значе­ние которой является оценкой параметра θ.

Для получения доверительного интервала наименьшей дли­ны при данном объеме выборки п и заданной доверительной веро­ятности 1 -α в качестве оценки 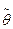параметра θ следует брать эффективную либо асимптотически эффективную оценку.

Рассмотрим один из методов построения доверительных интервалов. Предположим, что существует статистика Y = Y( 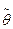, θ) такая, что:

а) закон распределения Y известен и не зависит от θ;

б) функция Y( 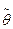, θ) непрерывна и строго монотонна по θ.
Пусть (1 -α) - заданная доверительная вероятность, а у_а/2 и у_1-a/2 - квантили распределения статистики Y порядков α/2 и 1 -α/ 2соответственно. Тогда с вероятностью 1 -α выполняется неравенство у_а/2 < Y( 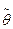, θ) < у_1-a/2.

Решая это неравенство относительно θ, найдем границы θ _i и θ ₂ доверительного интервала для θ. Если плотность распреде­ления статистики Y симметрична относительно оси Оу, то доверительный интервал имеет наименьшую длину, а если это распре­деление несимметрично, то длину, близкую к наименьшей.

Пример 46. Пусть х₁,х₂,...,х_n - выборка из нормально рас­пределенной генеральной совокупности. Найти доверительный интервал для математического ожидания т при условии, что дис­персия генеральной совокупности известна и равна σ², а довери­тельная вероятность равна 1 -α.

Решение. В качестве оценки математического ожидания т возьмем выборочное среднее . Для нормально распределенной генеральной совокупности выборочное среднее является эффективной оценкой т. Выборочное среднее 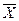в данном случае имеет нормальное распределение .

Рассмотрим статистику , имеющую нормальное распределение N (0,1) независимо от значения параметра т. Кро­ме того, U как функция т непрерывна и строго монотонна. Тогда 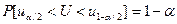, где и_а/2 и и_1-a/2 - квантили нормального распределения N (0,1).

Решая неравенство относительно т, по­лучим, что с вероятностью 1 -α выполняется условие:

.

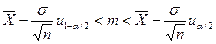Так как квантили нормального распределения связаны со­отношением и_а/2=-u_1-a/2, полученный доверительный интервал для т можно записать следующим образом:

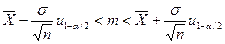
11.2. Доверительные интервалы для вероятности успеха в схеме Бернулли

и параметра λ распределения Пуассона.

Если распределение генеральной совокупности не является нор­мальным, то в некоторых случаях по выборкам большого объема можно построить доверительные интервалы для неизвестных па­раметров приближенно, используя при этом предельные теоремы теории вероятности и вытекающие из них асимптотические рас­пределения и оценки.

Пример 47. Пусть в n независимых испытаниях успех на­ступил х раз. Найти доверительный интервал для вероятности р успеха в одном испытании.

Решение. Эффективной оценкой вероятности успеха р в од­ном испытании является относительная частота = h = x/h. По теореме Муавра-Лапласа относительная частота h имеет асимпто­тически нормальное распределение , где q = 1 - р.

Рассмотрим статистику 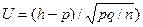, которая имеет асимптотически нормальное распределение N (0,1) независимо от значения р. При больших п тогда имеем

.

Отсюда получим, что с вероятностью ≈1 -α выполняется неравенство

.

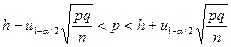Заменяя значения р и q влевой и правой частях записанно­го выше неравенства их оценками = h и = 1 -h, получим до­верительный интервал для вероятности успеха в схеме

.

Пример 48. При проверке 100 деталей из большой партии обнаружено 10 бракованных деталей.

а) Найти 95 % приближенный доверительный интервал для доли бракованных деталей во всей партии.

б) Какой минимальный объем выборки следует взять для того, чтобы с вероятностью 0,95 можно было утверждать, что до­ля бракованных деталей по всей партии отличается от частоты
появления бракованных деталей в выборке не более чем на 1 %?

Решение. а) Оценка доли бракованных деталей в партии по выборке равна = h = 10/100 = 0,1. По таблице приложений (П1) находим квантиль и_1-a/2 = и _0,975 = 1,96. Тогда 95% доверительный

интервал для доли бракованных деталей в партии приближенно имеет вид 0,041 < р < 0,159.

б) Представим полученный доверительный интервал в виде неравенства

,

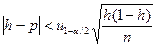которое выполняется с вероятностью ≈1 - α = 0,95. Так как со­гласно условию задачи , то для определения n полу­чим неравенство

.

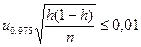Отсюда следует, что и n ≥(0,3·196)² =3457,44. Итак, минимальный объем выборки n = 3458.

11.3. Доверительные интервалы для коэффициента корреляции ρ.

Пусть выборка (х_i,у_i), i = 1,2,..., п, получена из генеральной совокупности, имеющей двумерное нормальное распределение, и r - выборочный коэффициент корреляции. При достаточно больших n статистика 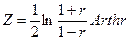имеет приближенно нормальное распределение .

Доверительный интервал для Arth ρ имеет вид

.

Доверительный интервал для ρ вычисляется с помощью таблиц гиперболического тангенса ρ= th z. (смотри таблицу при­ложение П8).

Пример 49. Выборочный коэффициент корреляции, вычис­ленный по выборке объема 10, r = -0,64. Найти 90 % доверительный интервал для коэффициента корреляции р.

Решение. По таблице приложений (П8) находим Arth(-0,64)= -Arth0,64 = -0,76.

Так как и_{0, 95} = 1,645, то доверительный интервал для Arthρ имеет вид 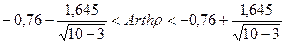, т.е. -1,38 <Arthρ< -0,14.

Обращаясь к таблице П8, получим 90 % доверительный ин­тервал для коэффициента корреляции: - 0,881 < ρ < -0,139.

11.4. Примеры доверительных интервалов.

1. Доверительный интервал для математического ожидания а нормальной случайной величины при известной дисперсии σ² имеет вид .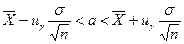

Здесь 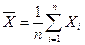величина определяется по заданной доверительной вероятности γ по таблице значений , в которой .

2. Доверительный интервал для математического ожидания а нормальной случайной величины при неизвестной дисперсии σ ² имеет вид ,

где оценка вычисляется по формуле 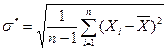, а величина определяется по заданной доверительной вероятно­сти γ объему выборки n с помощью таблицы значений .

3. Доверительный интервал для дисперсии σ ² нормальной случайной величины имеет вид

,

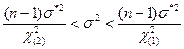где п - объем выборки; - оценка величины σ, определяемая формуло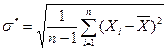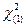й ; и 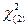- корни уравнений 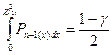, , 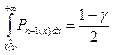в которых подынтегральная функция Р_п-х (х) является плотностью распределения хи-квадрат с n -1 степенями свободы.

Уравнения и 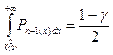при заданной доверительной вероятности γ решаются, используя таб­лицы приложений. При определении 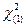входами этой таблицы

служат v = п -1 и 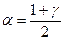, при определении 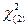- v = п -1 и .

4. Пусть п - число независимых испытаний, т - число на­ступлений события А, р - вероятность наступления события А в каждом отдельном испытании.

Рассмотрим случай, когда п достаточно велико, а значение р не слишком близко к нулю или к единице так, что можно восполь­зоваться асимптотикой Муавра-Лапласа. Доверительный интервал для р имеет вид р₁< р< р₂, где , ,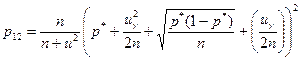

и_γ - определяется по заданной доверительной вероятности γ с помощью таблицы - приложений значений квантилей. Рассмот­рим случай т = 0. Тогда нижняя доверительная граница равна нулю, верхняя 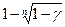. Если т = п, то нижняя и верхняя дове­рительные границы равны соответственно 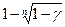и единице.

Дата добавления: 2014-11-20