Методы статистического описания результатов наблюдений 1 страница

Элементы математической статистики.

9.1. Основные задачи математической статистики

Установление закономерностей, которым подчинены массо­вые случайные явления, основано на изучении методами теории вероятностей статистических данных - результатов наблюдений.

Первая задача математической статистики - указать спосо­бы сбора и группировки статистических сведений, полученных в результате наблюдений или в результате специально поставлен­ных экспериментов.

Вторая задача математической статистики - разработать ме­тоды анализа статистических данных в зависимости от целей ис­следования. Здесь:

а) оценка неизвестной вероятности события; оценка пара­метров распределения, вид которого известен; оценка зависимо­сти случайной величины и др.;

б) проверка статистических гипотез о виде неизвестного распределения или о величине параметров распределения, вид которого известен.

Современная математическая статистика разрабатывает спо­собы определения числа необходимых испытаний до начала ис­следования (планирование эксперимента), в ходе исследования (последовательный анализ), и решает многие задачи. Математическая статистика определяется как наука о принятии решений в условиях неопределенности.

Задачи математической статистики помогают создавать ме­тоды сбора и обработки статистических данных для получения научных и практических выводов.

9.2. Выборка, способы её представления.

Математическая статистика позволяет получать обоснованные выводы о параметрах, видах распределений и других свойствах случайных величин по конечной совокупности наблюдений над ними - выборке.
В практике статистических наблюдений различают два вида наблюдений: сплошное (изучаются все объекты совокупности) и несплошное, выборочное (изучается часть объектов).
Вся подлежащая изучению совокупность объектов (наблюдений) называется генеральной совокупностью.

Понятие генеральной совокупности в определенном смысле аналогично понятию случайной величины (закону распределения вероятностей, вероятностному пространству), так как полностью обусловлено определенным комплексом условий.

Часть объектов, отобранная для непосредственного изученияиз генеральной совокупности, называется выборочной сово­купностью, или выборкой. Числа объектов (наблюдений) в генеральной или выборочной совокупности называются их объемами. Генеральная совокупность может иметь как конечный, так и бесконечный объем.

Сущность выборочного метода состоит в том, чтобы по некоторой части генеральной совокупности (по выборке) выносить суждение о её свойствах в целом.

Преимущество выборочного метода по сравнению со сплошным состоит в следующем:
- позволяет экономить затраты ресурсов;

- является единственно возможным в случае бесконечной генеральной совокупности или в случае, когда исследование связано с уничтожением наблюдаемых объектов;

- дает возможность углубленного исследования за счет рас­ширения программы исследования;

- позволяет снизить ошибки регистрации, т.е. расхождение между истинным и зарегистрированным значениями признака.

Основной недостаток выборочного метода - ошибки иссле­дования, называемые ошибками репрезентативности (представи­тельства).

Различают следующие виды выборок:

- собственно-случайная выборка, образованная случайным выбором элементов без расчленения на части или группы;

- механическая выборка, в неё элементы из генеральной со­вокупности отбираются через определенный интервал;

- типическая (стратифицированная) выборка, в которую слу­чайным образом отбираются элементы из типических групп;

- серийная (гнездовая) выборка, в которую случайным обра­зом отбираются не элементы, а целые группы совокупности, при­чем сами серии подвергаются сплошному наблюдению.

Используют два способа образования выборки:

- повторный отбор (по схеме возвращенного шара), когда каждый элемент, случайно отобранный и обследованный, возвра­щается в общую совокупность и может быть повторно отобран;

- бесповторный отбор (по схеме невозвращенного шара), когда отобранный элемент не возвращается в общую совокуп­ность.

Итак, закон распределения некоторой случайной величины X называется распределением генеральной совокупности, а слу­чайный вектор (X₁,...,X_n) - выборочным вектором. Числа х₁,..., х_п, получаемые на практике при n -кратном повторении некоторо­го эксперимента в неизменных условиях, представляют собой реализацию выборочного вектора и есть выборка (х₁,х₂,...,х_п) объ­ема п.

Выборку (х₁,х₂,...,х_п) при необходимости можно рассмат­ривать как точку выборочного пространства, т. е. множества, на котором задано распределение выборочного вектора (Х₁,Х₂,...,Х_n).

Аналогично определяется выборка в случае, когда некото­рый случайный эксперимент связан с несколькими случайными величинами. Так, выборка объема п из двумерной генеральной совокупности есть последовательность (х₁, у₁),...,(х_n,у_n) пар значений случайных величин X и Y, принимаемых ими в п неза­висимых повторениях некоторого случайного эксперимента.

Вариационным рядом выборки х₁,х₂,...,х_п называется способ ее записи, при котором элементы упорядочиваются по ве­личине, т е. записываются в виде последовательности х ⁽¹⁾, х ⁽²⁾,…, х⁽ⁿ⁾, где х⁽¹⁾≤х⁽²⁾≤...≤х⁽ⁿ⁾.

Разность между максимальным и минимальным элементами выборки x ^(max) - x ^(min) =ωназывается размахом выборки. Пусть выборка (х₁,х₂,...,х_п) содержит k различных чисел z₁,z₂,...,z_k, причем z_i встречается n_i раз (i = 1,2, ...,k). Число n_i называют частотой элемента выборки z_i. Следует заметить, что .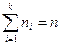

Статистическим рядом называют последовательность пар (z_i,n_i). Статистический ряд записывают в виде таблицы, в первой строке которой находятся элементы z_i, а во второй - их частоты.

Пример 28. Записать в виде вариационного и статистического рядов выборку 5, 3, 7, 10, 5, 5, 2, 10, 7, 2, 7, 7, 4, 2, 4. Определить размах выборки.

Решение. В данном случае объем выборки n = 15. Упорядочим элементы выборки по величине, получим вариационный ряд 2, 2, 3, 4, 4, 5, 5, 5, 7, 7, 7, 7, 10, 10. Найдем размах выборки ω=10-2= 8. Различными в заданной выборке являются элементы z₁ = 2, z₂ =3, z₃ = 4, z₄ = 5, z₅ = 7, z₆ = 10; их частоты соответственно равны n₁ = 3, n₂ =1, n₃ = 2, n₄ = 3, n₅ = 4, n₆ = 2. Статистический ряд исходной выборки можно записать в виде следующей таблицы:

zi
ni

Для контроля правильности записи находим 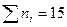. При большом объеме выборки ее элементы рекомендуется объединять в группы (разряды), представляя результаты опытов в виде группированного статистического ряда. В этом случае ин­тервал, содержащий все элементы выборки, разбивается на k не­пересекающихся интервалов. Вычисления упрощаются, если эти интервалы имеют одинаковую длину . В дальнейшем рассматривается именно этот случай. После того как частичные ин­тервалы выбраны, определяют частоты - количество n_i элементов выборки, попавших в i -й интервал (элемент, совпадающий с верх­ней границей интервала, относится к следующему интервалу). Получающийся статистический ряд в верхней строке содержит середины z_i интервалов группировки, а в нижней — частоты n_i (i = 1,2,..., k).

Наряду с частотами одновременно подсчитываются также накопленные частоты 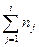, относительные частоты n_i /п и накопленные относительные частоты , i = 1,2,..., k. Полученные результаты сводятся в таблицу, называемую таблицей час­тот группированной выборки.

Следует помнить, что группировка выборки вносит по­грешность в дальнейшие вычисления, которая растет с уменьше­нием числа интервалов.

Пример 29. Представить выборку 55 наблюдений в виде таблицы частот, разбив имеющиеся данные выборки на семь ин­тервалов группировки. Выборка:

20,3	15,4	17,2	19,2	23,3	18,1	21,9
15,3	16,8	13,2	20,4	16,5	19,7	20,5
14,3	20,1	16,8	14,7	20,8	19,5	15,3
19,3	17,8	16,2	15,7	22,8	21,9	12,5
10,1	21,1	18,3	14,7	14,5	18,1	18,4
13,9	19,1	18,5	20,2	23,8	16,7	20,4
19,5	17,2	19,6	17,8	21,3	17,5	19,4
17,8	13,5	17,8	11,8	18,6	19,1

В данном случае размах выборки ω =23,8 -10,1 = 13,7; тогда длина интервала группировки будет b = 13,7/7≈2. В качестве первого интервала возьмем интервал 10 - 12. Результаты группи­ровки сведем в таблицу 1

Таблица 1

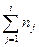
Номер интерва­ла i	Границы интервала	Середина интервала zi	Частота ni	Накоп­ленная частота	Относи­тельная частота ni /п	Накопленная относительная частота
	10-12		2		0,0364	0 0364
	12-14				0,0727	0 1091
	14-16				0,1455	0 2546
	16-18				0,2182	0,4728
	18-20				0,2909	0 7637
	20-22				0,1818	0,9455
	22-24				0,0545	1,0000

9.3. Функция распределения.

Пусть (х₁,х₂,...,х_п) - выборка из генеральной совокупности с функцией распределения F_x(x). Распределением выборки назы­вается распределение дискретной случайной величины, принимающей значения х₁,х₂,...,х_п с вероятностями 1/ n. Соответст­вующую функцию распределения называют эмпирической (выбо­рочной) функцией распределения и обозначают .

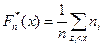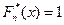Эмпирическую функцию распределения определим по зна­чениям накопленных частот соотношением , здесь суммируются частоты тех элементов выборки, для которых вы­полняется неравенство z_i < х. Тогда получим, что при х≤х⁽¹⁾ и при х>х⁽ⁿ⁾. На промежутке (х⁽¹⁾; х⁽ⁿ⁾ ] представляет собой неубывающую кусочно-постоянную функцию.

Аналогично определяем эмпирическую функцию распреде­ления для группированной выборки.

Значение эмпирической функции распределения для стати­стики определяется следующим утверждением.

Теорема (Гливенко). Пусть - эмпирическая функция распределения, построенная по выборке объема п из генеральной совокупности с функцией распределения F_x(x). Тогда для любо­го х Î (- ∞,+∞) и любого ε > 0

.

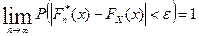Таким образом, при каждом х сходится по вероятно­сти к F_x(x) и при большом объеме выборки может служить при­ближенным значением (оценкой) функции распределения генеральной совокупности в каждой точке х.

9.4. Гистограмма и полигон.

Для наглядного представления выборки можно использо­вать гистограмму и полигон частот.

Гистограммой частот группированной выборки называет­ся кусочно-постоянная функция, постоянная на интервалах группировки и принимающая на каждом из них значения ,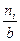

i = 1,2,..., k соответственно. Площадь ступенчатой фигуры под графиком гистограммы равна объему выборки п.

Аналогично определяется гистограмма относительных частот. Площадь соответствующей ступенчатой фигуры для нее равна единице.

При увеличении объема выборки и уменьшении интервала группировки гистограмма относительных частот является стати­стическим аналогом плотности распределения f_x(x) генеральной совокупности.

Полигоном частот называется ломаная с вершинами в точках 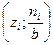, где i = 1,2,..., k, а полигоном относительных частот - ломаная с вершинами в точках 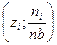, где i = 1,2,..., k. Имеем, что полигон относительных частот получается из полигона частот сжатием по оси Оу в п раз.

Если плотность распределения генеральной совокупности является достаточно гладкой функцией, то полигон относитель­ных частот является более хорошим приближением плотности, чем гистограмма.

Пример 30. Построить гистограмму и полигон частот, а также график эмпирической функции распределения группиро­ванной выборки из примера 29.

Решение. По результатам группировки (см. таблицу 1.) строим гистограмму частот (рис. 7). Соединяя отрезками ломаной середины верхних оснований прямоугольников, из которых со­стоит полученная гистограмма, получаем соответствующий поли­гон частот (рис. 8).

Так как середина первого интервала группировки z₁ = 11, то при х ≤ 11. Рассуждая аналогично, находим, что 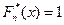при х > 23. На полуинтервале (11,23] эмпирическую функцию распределения строим по данным третьего и последнего столбцов таблицы 1.

Рис.7 Рис.8

имеет скачки в точках, соответствую­щих серединам интервалов группировки. В результате получаем график , изображенный на рис. 9.

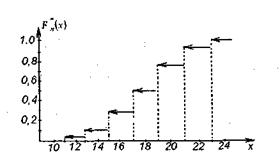
Рис.9

9.5. Метод моделирования.

В задачах статистического анализа сложных систем, напри­мер, при разработке систем автоматического проектирования (САПР), широко используется метод моделирования выборки из генеральной совокупности с заданным законом распределения.

Пусть случайная величина X имеет функцию распределения F_x (x). Как известно из теории вероятностей случайная величина Y = F_x(x) имеет равномерное распределение R (0,l). Отсюда сле­дует, что случайная величина X может быть получена из равно­мерно распределенной случайной величины Y по формул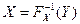е , где 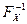- функция, обратная к F_x (заведомо сущест­вующая для случайных величин непрерывного типа).

Метод моделирования выборки из генеральной совокупно­сти с законом распределения F_x(x) реализуется следующим ал­горитмом: , j = 1,2,..., n, где у₁, у₂,..., у_n - выборка из

генеральной совокупности с равномерным распределением R (0,1), являющаяся последовательностью случайных чисел.

Случайные числа у₁, у₂,..., у_n можно получить, выбрав слу­чайным образом n чисел из таблицы- приложений П12 (см. в кон­це учебного пособия) и разделив каждое выбранное число на 100. При наличии любого вычислительного устройства случайные чис­ла у₁, у₂,..., у_n генерируются с помощью формулы 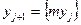, jÎN, где {а} - дробная часть числа a, a m- простое число, большее де­сяти. В качестве начального значения у₁ в записанной выше фор­муле можно выбрать произвольное число из интервала (0,l) с не­нулевыми разрядами в десятичной системе счисления. От удачно­го выбора начального значения у_х зависит качество последова­тельности у₁, у₂,..., у_n.

Этот алгоритм получения выборки из генеральной сово­купности с законом распределения F_x(x) поясняется на рис. 10.

Рис. 10.

Для получения выборки из генеральной совокупности, рас­пределенной по закону N (0,1), можно воспользоваться алгорит­мом, основанным на любом из следующих соотношений:

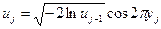, j = 2,3,..., n,

,

где, как и выше, у₁,у₂,...,у_п - выборка из генеральной совокупно­сти с равномерным распределением R (0,1).

9.6. Числовые характеристики выборочного распределения.

Пусть х₁,х₂,...,х_п -выборка объема п из генеральной сово­купности с функцией распределения F_x(x). Рассмотрим выбо­рочное распределение, т. е. распределение дискретной случайной величины, принимающей значения х₁,х₂,...,х_п с вероятностями, равными 1 /п. Числовые характеристики этого выборочного рас­пределения называются выборочными (эмпирическими) число­выми характеристиками. Следует отметить, что выборочные чи­словые характеристики являются характеристиками данной выборки, но не являются характеристиками распределения гене­ральной совокупности. Чтобы подчеркнуть это различие, выбо­рочные характеристики в дальнейшем будем обозначать теми же символами, что и случайные величины, но со значком * наверху. Некоторые выборочные характеристики имеют традиционные обозначения, например, - выборочное среднее.

Пример 31. Найти формулы, определяющие выборочные математическое ожидание и дисперсию для негруппированной выборки объема п.

Решение. Математическое ожидание дискретной случайной величины определяется по формуле

.

Так как для выборочного распределения р_j = 1/ n, то .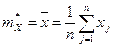

Аналогично будем иметь выборочную дисперсию .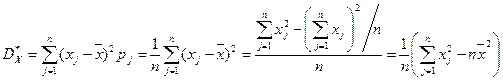

Выборочной модой 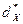унимодального (одновершинного) распределения называется элемент выборки, встречающийся с наибольшей частотой.

Выборочной медианой называется число 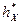, которое делит вариационный ряд на две части, содержащие равное число эле­ментов.

Если объем выборки п — нечетное число (т.е. п = 2l +1), то 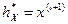, то есть является элементом вариационного ряда со средним номером. Если же п = 2 l, то .

Пример 32. Определить среднее, моду и медиану для вы­борки 5, 6, 8, 2, 3, 1, 1, 4.

Решение. Представим данные в виде вариационного ряда: 1, 1, 2, 3, 4, 5, 6,8. Выборочное среднее 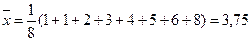. Все элементы входят в выборку по одному разу, кроме 1, следовательно, мода . Так как п = 8, то медиана .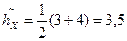

Итак, , , .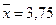

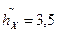Для упрощения вычислений выборочных среднего и дис­персии группированной выборки, эту выборку преобразуют так: , i= 1,2,..., k,где 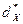- выборочная мода, а b - длина интервала группировки. Эти соотношения показывают, что в выборку z₁ ,z₂,...,z_n внесена систематическая ошибка 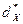, а ре­зультат подвергнут преобразованию масштаба с коэффициентом k = 1/b. Полученный в результате набор чисел u₁ ,u₂,...,u_n можно рассматривать как выборку из генеральной совокупности 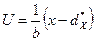. Тогда выборочные среднее и дисперсия исходных данных связаны со средним 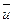и дисперсией 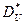преобра­зованных данных следующими соотношениями: , .

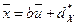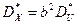Пример 33. Вычислить среднее и дисперсию группирован­ной выборки

Границы интервалов	134-138	138-142	142-146	146-150	150-154	154-158
Частоты

Решение. Длина интервала группировки b = 4, значение се­редины интервала, встречающегося с наибольшей частотой 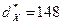. Преобразование последовательности середин интервалов выполняется по формуле:

, где i = 1,2,...,6.

Таблица 2

i	zi	ui	ni	ni ui	ni ui^2	ni (ui +1)^2
		-3		-3
		-2		-6
		-1		-15
	-	-		-6

Вычисления сведены в таблицу 2. Последний столбец этой таблицы служит для контроля вычислений при помощи тождества .

Выполняя вычисления, получим 58 + 2 · (-6) + 23 = 99.

Полученный результат показывает, что вычисления выпол­нены правильно. По формулам, данным выше, находим средние значения U

, .

Далее находим средние данной выборки:

, .

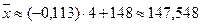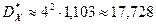9.7. Выборочные коэффициенты асимметрии, эксцесса. Квантиль.

Выборочные коэффициенты асимметрии и эксцесса вычис­ляются по формулам , .

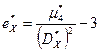Вычисление выборочных коэффициентов асимметрии и экс­цесса для группированной выборки значительно упрощается, если данные предварительно преобразовать. При этом используют сле­дующие формулы:

,

.

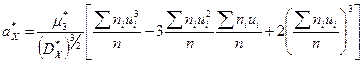Для контроля подсчета сумм , l = 1,2,3,4 вычисляют отдельно правую и левую части тождества 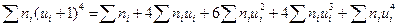. Результаты вычислений следует оформить в виде таблицы.

Дата добавления: 2014-11-20