Ядерная модель атома. Формула резерфорда. 4 страница

Спин – квантовая характеристика, не имеющая классических аналогов и являющаяся внутренним свойством квантовых объектов, характеризующая их равноправно с такими величинами, как масса или электрический заряд.

С точки зрения теоретической физики спин – это дополнительная степень свободы квантовой частицы.

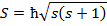
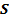- спин, собственный механический момент

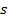- спиновое квантовое число, характеризующее ту или иную частицу

Спин в отличии от орбитального механического момента строго фиксирован для данной частицы и принимает единственное значение.

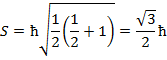
Но его проекция также, как и орбитального момента – квантуется.

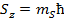
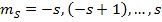- магнитное спиновое квантовое число

Гиромагнитное отношение для спиновых моментов:

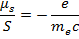
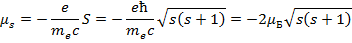
Говорят, что спиновый момент обладает удвоенным магнетизмом, этот факт – одно из доказательств того, что спин нельзя представить, как вращение частицы относительно собственного диаметра.

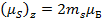- проекция магнитного спинового момента квантуется и у электрона может принимать два значения:

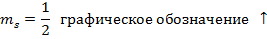
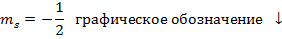
Т.о. магнитный момент атома складывается из трех составляющих:

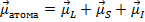
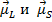- магнитные моменты орбитальной оболочки

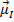- магнитный момент ядра. В атомной физике обычно не учитывается ввиду малости по сравнению с магнитными моментами электронной оболочки.

Опыты Штерна и Герлаха доказали существование у атомов магнитных моментов, явление их квантования, а также существование спина электрона.

Схема эксперимента Штерна и Герлаха.

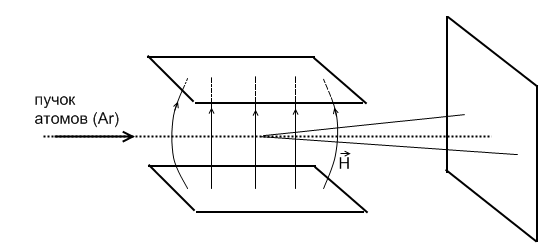
Серебро было выбрано, т.к. у него один валентный электрон. Между пластинами создавалось магнитное поле 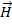, сильно неоднородное на атомных расстояниях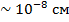

Было установлено, что пучек атомов серебра расщеплялся относительно начального направления на два симметричных пучка, это расщепление связано с взаимодействием магнитных моментов атомов и приложенного магнитного поля.

Дополнительная энергия, приобретаемая атомом в магнитном поле:

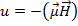
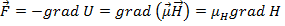
Если бы проекция момента не квантовалась, то в силу неравенства:

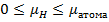
мы бы наблюдали на экране сплошную полосу. В действительности на экране наблюдались отдельные пятна. Т.о. было доказано явление квантования магнитных и механических моментов.

Покажем, что из опыта Штерна и Герлаха следует существование спина у электрона.

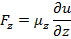
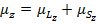
Предположим, что 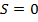, тогда 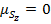, тогда:

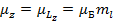
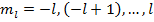
Всего 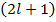значений 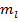при любых 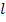нечетное, т.е. пучок должен разбиваться на 1, 3, 5, …

Для объяснения четного количества компонент на экране рассмотрим атом серебра с одним валентным электроном на внешней оболочке.

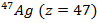
Для атома серебра в основном состоянии орбитальное квантовое число 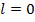. Тогда 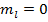, 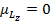. В данном случае магнитный момент чисто спиновый.

Т.к. для одного электрона на внешней оболочке возможно всего две проекции 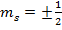спинового момента, то весь пучок разбивается на две компоненты.

Глава: Теория атомов и молекул.

§28. Спектр атома водорода.

Для атома водорода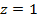

Потенциальная энергия в кулоновском поле ядра:

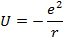
Запишем УШ для атома водорода (единственное уравнение атомной физики, которое можно решить аналитически):

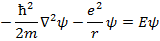
Для решения данного уравнения необходимо перейти к сферической СК, при этом УШ решается методом разделения переменных и решение имеет следующий вид:

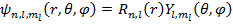
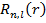– радиальная часть

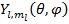- сферические или шаровые функции

УШ допускает два типа решений:

1) 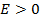, энергия принимает любые положительные значения, соответствует инфинитному движению электрона, т.е. когда не существует атома, а есть система протон-электрон.

2) 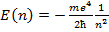– спектр энергий атома в связанном состоянии.

Энергия водорода зависит только от главного квантового числа, в то время как волновая функция определяется тремя числами 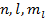, уровни энергии атома водорода вырождены по орбитальному и магнитноорбитальному квантовым числам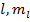

Пример.

Пусть водород находится в первом состоянии.

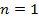
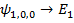
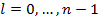
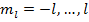
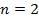
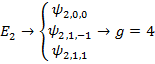
Второй энергитический уровень водорода четырехскоростно вырожден.

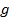-статистический вес уровня или кратность его вырождения, количество различных состояний системы, при которых ее энергия одинакова.

Вырождение по орбитальному квантовому числу для водорода случайно, т.к. электростатическое поле протона и электрона – кулоново.

Независимость энергии от 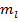связано с изотропией пространства. Изотропию можно нарушить, создавая магнитное или электрическое поле, при этом вырождение по 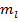снимается.

Найдем кратность вырождения уровня энергии водорода. Любому квантовому числу 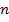соответствует 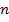значений 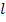, каждому из которых отвечает 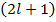значений 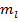, т.о. для любого зафиксированного 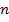кратность вырождения:

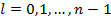
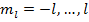
С учетом спина электрона:

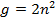
В спектроскопии уровни энергии атомов обозначают:

1)

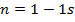
2)

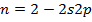
3)

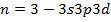
Обобщенная формула Бальмера для спектроскопии волнового числа:

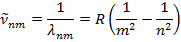
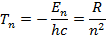
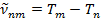
Схема уровней атома водорода.

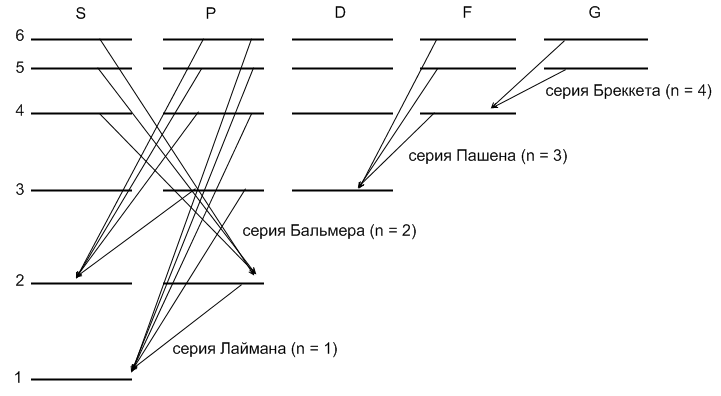
Правила отбора для радиационных переходов являются следствием закона сохранения четности, а также закона сохранения момента импульса в дипольном приближении.

Правила отбора заключаются в следующем. При радиационных переходах возможны следующие изменения квантовых чисел.

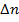– может изменяться произвольно

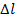- на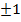

Таким образом S уровни комбинируют только с P уровнями.

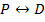
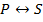
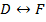
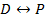
Рассмотрим волновые функции атома водорода:

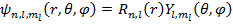
Сферические функции 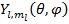являются собственными функциями оператора квадрата момента импульса 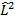, при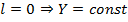

Рассмотрим плотность вероятности

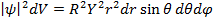
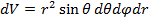
Вероятность обнаружить электрон на расстоянии 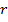от протона при данных 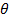и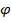

§29. Щелочные металлы.

Щелочные металлы образуют первую группу периодической системы элементов и имеют один валентный электрон на внешней оболочке. Внутренние электроны и ядро атома щелочного металла образуют прочный остов.

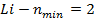
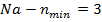
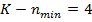
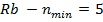
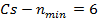
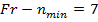
В случае щелочного металла электростатическое поле, как и у водорода, сферически симметрично, но уже не кулоново. Если внешний электрон находится на значительном расстоянии от остова, то он движется в поле с эффективным электрическим зарядом 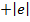. При проникновении внешнего электрона в остов, он поляризуется и его эффективный заряд изменяется, поэтому потенциальную энергию валентного электрона можно представить:

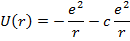
- поле точечного заряда

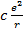- поле диполя

Подставляя данную формулу потенциальной энергии в УШ и решая последнее, получаем спектр энергии щелочного металла:

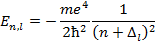
Энергия зависит от двух квантовых чисел 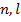, что связано с некулоновостью поля.

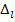- квантовый дефект или поправка Ридберга.

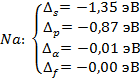
Для водородоподобного атома:

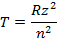
Для щелочных металлов:

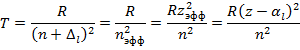
- зарядовое число

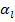- постоянная экранирования заряда ядра

Правила отбора для щелочных металлов.

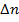– любое

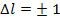
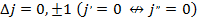
Схема уровней атома натрия:

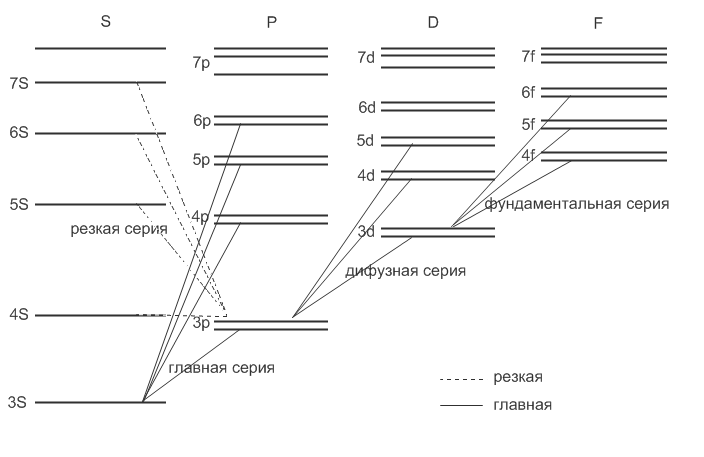
Основные серии щелочного металла:

1) Главная.

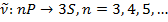
2) Вторая побочная (резкая)

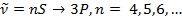
3) Первая побочная (диффузная)

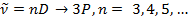
Опытным путем было установлено, что спектральные линии щелочных металлов дублетны (двойные), что связано с тем, что во всех состояниях, кроме 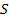, уровни энергии расщепляются на два уровня. Данное расщепление является следствием спин-орбитального взаимодействия.

Под спин-орбитальным взаимодействием понимают взаимодействие магнитного орбитального момента электрона с его спиновым магнитным моментом, в результате чего появляется зависимость энергии атома от спинового квантового числа.

Т.к. в 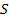- состоянии 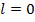, то спин-орбитального взаимодействия в данном случае нет и уровни энергии одинарные.

§. Общая векторная модель атома.

Электроны в атоме имеют орбитальные 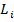и спиновые 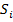механические моменты, которые складываются в общий или полный механический момент импульса атома:

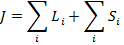
Складывать эти вектора можно различными способами.

Первый способ. 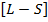– связь (нормальная связь)

Данный способ реализуется для атомов легких элементов, при этом кулоново отталкивание электронов преобладает над спин-орбитальным взаимодействием. В результате чего каждый электрон обладает собственным орбитальным 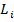и спиновым 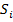механическими моментами, которые, складываясь по раздельности, дают результирующий орбитальный и спиновый механические моменты атома.

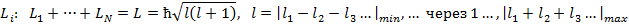
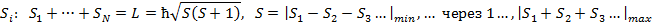
Полный механический момент атома также по квантовым законам определяется, как сумма орбитального и спинового момента.

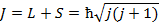
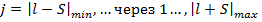
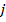- полное (внутреннее) квантовое число.

Как правило, 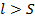, поэтому вводят характеристику:

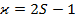
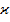– мультиплетность уровня, число, показывающее, каким количеством способов спин может быть ориентирован относительно орбитального момента. Другими словами, мультиплетность – число подуровней тонкой структуры, соответствующее каждому уровню с данным числом 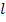(за исключением 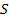-уровней, у которых ).

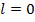Для атомов с одним валентным электроном, спиновое квантовое число 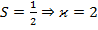и уровни таких атомов двойные или дублетные.

Полный механический момент:

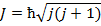
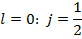
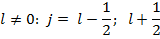
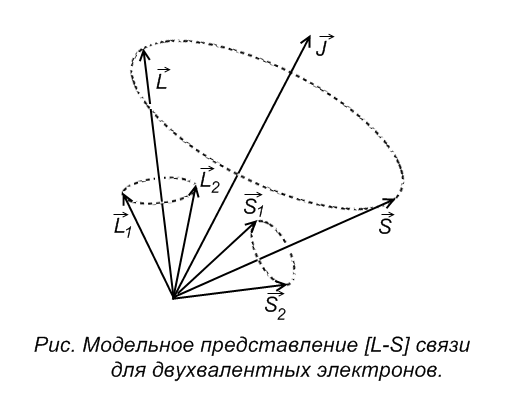
Векторы и прецессируют вокруг 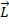, векторы 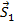и 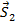прецессируют вокруг 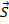. При этом суммарные векторы 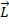и 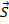при сложении также прецессируют вокруг вектора .

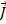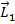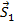и ; и 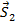– быстрые прецесси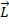и.

и 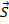- медленная прецессия.

В центральном поле сохраняется только вектор 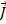- полный момент импульса, векторы 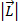и 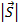при этом сохраняются только по модулю, но меняют свое направление. Если поместить такой атом в МП, т.е. задать выделенное направление в пространстве, то сохраняться будет только проекция полного момента на выделенное направление.

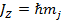
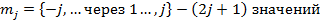
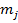- магнитное внутреннее квантовое число.

Если внутренние оболочки атома полностью заполнены, то моменты импульсов внутренних электронов полностью скомпенсированы 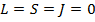. Т.о. в общей векторной модели атома учитываются только механические и магнитные моменты легких электронов в незаполненных оболочках.

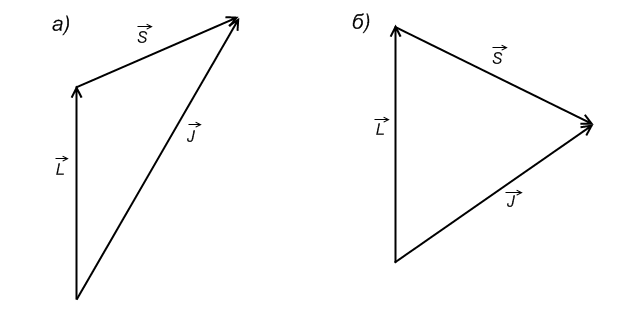
Второй способ. 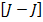- связь.

Характерен для тяжелых атомов с большим количеством валентных электронов, в данном случае, спин-орбитальное взаимодействие каждого электрона преобладает над электростатическим отталкиванием электронов между собой, в результате чего у каждого из них есть полный механический момент.

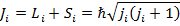
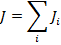
Все моменты складываются в общий механический момент.

Очевидно, что как и в случае 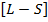– связи, число возможных значений 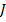такое же, но уровни энергии при этом будут отличаться, т.к. различна природа взаимодействия. При этом величины:

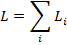
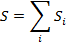
полностью теряют смысл.

§. Тонкая структура спектральных термов

щелочных металлов и атома водорода.

Тонкой структурой называют расщепление энергитических уровней в результате спин-орбитального взаимодействия.

Рассмотрим атом с одним валентным электроном.

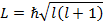
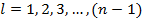
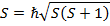
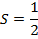
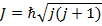
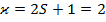
В спектроскопии для обозначения уровня энергии и соответствующего спектрального терма вводится следующая запись:

Например:

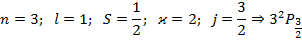
Таблица уровней.

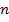
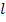
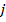
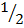
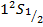
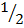
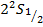
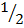
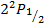
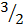
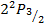
Для атома водорода уровни энергии вырождены по 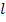, и, как следует из теории Дирака, для данных значени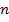й и 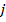, и разных 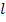уровни энергии совпадают.

Например:

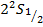
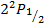
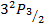
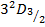
Рассмотрим термы водородоподобного атома с учетом тонкой структуры:

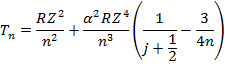
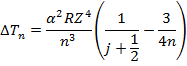
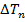- поправка к термам, учитывающая спин-орбитальное взаимодействие.

С ростом зарядового числа 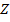, поправка 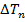увеличивается. С ростом главного квантового числа 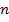, поправка 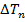уменьшается.

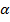– постоянная тонкой структуры.

§. Тонкая структура спектральных линий

щелочных металлов и атома водорода. Лэмбовский сдвиг.

1) Главная серия щелочных металлов.

Правила отбора:

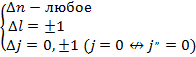
Рассмотрим .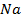

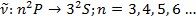
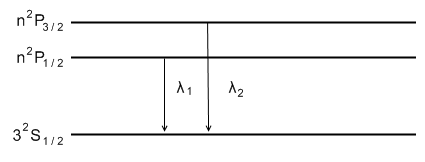
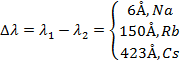
2) Резкая серия

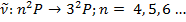
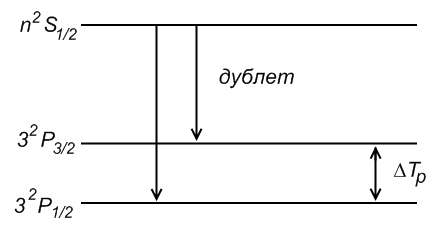
Дата добавления: 2014-11-20