Вычисление интеграла с заданной точностью

Формула Гаусса

Формула Гаусса также соответствует выражениям (2.7.2-2.7.4). Выглядит она идентично формуле (2.7.3):

(2.7.22)

Узлы x_i, аналогично, находятся согласно (2.7.4), а абсциссы точек интегрирования t_i являются нулями полинома Лежандра

(2.7.23)

Известно, что эти нули действительны, различны и лежат на отрезке [–1, 1]. Коэффициенты A_i определяются решением СЛАУ

(2.7.24)

Определитель этой системы есть определитель Ван­дер­мон­да

следовательно, система (2.7.24) имеет единственное решение.

Формула Гаусса является точной для всех полиномов до степени 2n–1 включительно.

Рассмотрим случай, когда необходимо вычислить интеграл с заданной точностью, при этом точное значение интеграла не известно. В этом случае сначала интеграл считается на некоторой начальной сетке с количеством интервалов интегрирования n₀ = n. Обозначим полученное значение интеграла как I₀. Затем, аналогично, на сетке с количеством интервалов n₁ = α·n₀ (α > 1) находим значение интеграла I₁. Считая, что значение I₁ найдено с большей точностью (т.к. сетка более частая), условно примем его за точное значение. Тогда относительную погрешность интегрирования можно оценить по формуле

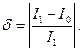(2.7.25)

Если она удовлетворяет заданной погрешности, то вычисления можно прекращать, иначе добавляем в сетку новые узлы и продолжаем процесс. В общем случае,

n_k = α·n_k–1 = α^k·n₀, (2.7.26)

а процесс завершается при

(2.7.27)

Для упрощения разбиения отрезка интегрирования на интервалы, часто полагают α = 2.

Примечания.

1. Формула для расчета относительной погрешности даст деление на ноль, если какой-либо из интегралов I_k получится равным нулю. Тогда погрешность интегрирования можно оценить по формуле для абсолютной погрешности:

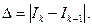(2.7.28)

2. Т.к. в методах Чебышева и Гаусса количество отрезков интегрирования влияет на размер системы уравнений для поиска коэффициентов, ограничимся вычислением интеграла с заданной точностью только для обязательных методов.

Дата добавления: 2014-11-20