Формула трапеций

Формулы прямоугольников

Методы решения

Предлагается реализовать четыре обязательных метода численного интегрирования функций – левосторонних и правосторонних прямоугольников, трапеций и Симпсона и, по желанию, один из двух дополнительных – Чебышева или Гаусса.

В формуле левосторонних прямоугольников полагаем, что на отрезке [x_i, x_i+1] функция φ_i(x) = 1, c_i = y_i (рис. 2.7.1).

Очевидно, что Ф_i(x) = x, k = n–1. Тогда из (2.7.1) получаем:

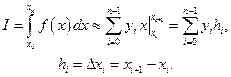(2.7.5)

Если сетка равномерная, то

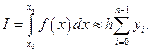(2.7.6)

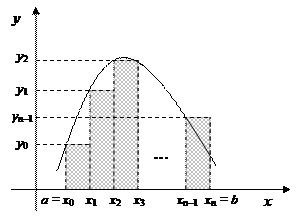
Рис. 2.7.1 – Интегрирование левосторонней формулой прямоугольников

В формуле правосторонних прямоугольников полагаем, что на отрезке [x_i, x_i+1] функция φ_i(x) = 1, c_i = y_i+1 (рис. 2.7.2).

Тогда Ф_i(x) = x, k = n–1, и из (2.7.1) получаем

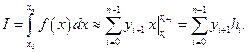(2.7.7)

Если сетка равномерная, то

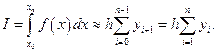(2.7.8)

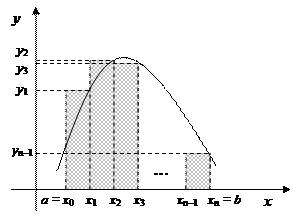
Рис. 2.7.2 – Интегрирование правосторонней формулой прямоугольников

В формуле трапеций полагаем, что функция на отрезке [x_i, x_i+1] заменяется прямой линией, соединяющей точки (x_i, y_i) и (x_i+1, y_i+1) (рис. 2.7.3).

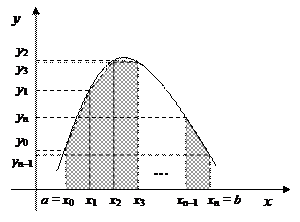
Рис. 2.7.3 – Интегрирование формулой трапеций

Несложно записать уравнение прямой, проходящей через две точки:

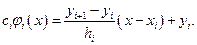
Интегрируем:

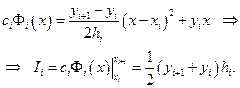(2.7.9)

Это же выражение можно легко получить из геометрических соображений (см. рис. 2.7.3).

Есть и еще один способ вывода данной формулы. Очевидно, что на каждом интервале функция заменяется полиномом первого порядка. Нам уже известны полиномы, интерполирующие табличную функцию по p+1 точке и дающие при этом степенной полином порядка p – это полиномы Ньютона и Лагранжа. Как уже было сказано, они являются разной формой записи одного и того же полинома, поэтому их применение даст одинаковый результат. Возьмем, например, полином Лагранжа. Тогда

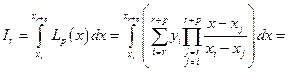
(2.7.10)

Здесь A^* – некоторые квадратурные коэффициенты. Если сетка равномерная, то делаем замену (2.5.9):

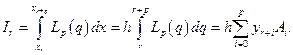(2.7.11)

Т.к. сетка равномерная, квадратурные коэффициенты не зависят от индекса r. Используем выражение (2.5.6) и введем новые коэффициенты H_i:

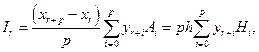(2.7.12)

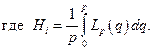(2.7.13)

Коэффициенты H_i называются коэффициентами Нью­то­на-Котеса. Для построения полинома первого порядка нужны всего две точки (т.е. p = 1), поэтому сетку можно считать равномерной. Интегрируя (2.7.13), получим

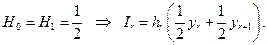(2.7.14)

Т.е. полученное выражение совпадает с (2.7.9). Остается только просуммировать по всем интервалам:

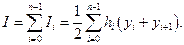(2.7.15)

Если сетка равномерная, то

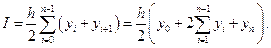(2.7.16)

Дата добавления: 2014-11-20