Формат выходных данных. Формат выходного файла: x0 y0 x1 y1 xm ym – значения искомой функции в узлах сетки (при t = 1 или t = 3); x0 y10 yp0 x1 y11 yp1

Формат выходного файла:

x0 y0 x1 y1 … xm ym	– значения искомой функции в узлах сетки (при t = 1 или t = 3);
x0 y10…yp0 x1 y11…yp1 … xm y1m…ypm	– значения искомых функций в узлах сетки (при t = 2);
ε	– СКО (если известно аналитическое решение).

2.9. Практическая работа №9 «Решение линейных интегральных уравнений»

Обязательных методов
Баллов за обязательные методы
Дополнительных методов
Баллов за дополнительные методы
Количество вариантов

Опять же, нет необходимости обосновывать очевидную потребность в численных методах решения уравнений. В данной практической работе будем рассматривать уравнения, содержащие интегралы. Ограничимся случаем, когда неизвестная функция входит в интеграл линейно, т.е. классом линейных интегральных уравнений (ЛИУ).

Уравнение вида

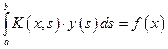(2.9.1)

называется ЛИУ Фредгольма 1-го рода. Здесь f (x) – правая часть, x принадлежит некоторому интервалу [c, d]; y(s) – искомая функция, s принадлежит некоторому интервалу [a, b]; K(x, s) – ядро уравнения, заданное на прямоугольнике [a ≤ s ≤ b, c ≤ x ≤ d].

Уравнение вида

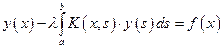(2.9.2)

называют ЛИУ Фредгольма 2-го рода. Здесь λ – некоторая константа, а x и s заданы на одинаковом интервале [a, b]. Соответственно, ядро задано на квадрате [a ≤ s ≤ b, a ≤ x ≤ b].

Дата добавления: 2014-11-20