
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Свойства функций, непрерывных на отрезке
|
|
|
|
Свойство I. Ограниченность непрерывной функции
ТЕОРЕМА 5.2 (Первая теорема Вейерштрасса). Пусть функция  определена и непрерывна на отрезке
определена и непрерывна на отрезке 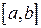 . Тогда на этом отрезке
. Тогда на этом отрезке  ограничена, то есть существует число
ограничена, то есть существует число  ,
,  такое, что
такое, что 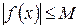 для всех
для всех  .
.
Доказательство. Доказательство проводим от противного. Пусть функция  не ограничена сверху на отрезке
не ограничена сверху на отрезке 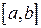 , то есть
, то есть 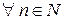 существует последовательность
существует последовательность 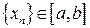 такая, что
такая, что 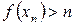 . Последовательность
. Последовательность  , то есть ограничена. По теореме Больцано-Вейерштрасса из последовательности
, то есть ограничена. По теореме Больцано-Вейерштрасса из последовательности  можно выделить сходящуюся подпоследовательность
можно выделить сходящуюся подпоследовательность 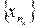 , такую что
, такую что  , где
, где 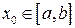 .
.
По условию функция  непрерывна на
непрерывна на 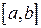 , следовательно, и в точке
, следовательно, и в точке 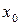 , то есть
, то есть 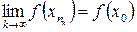 . Таким образом, последовательность
. Таким образом, последовательность 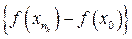 является бесконечно малой, что невозможно, так как
является бесконечно малой, что невозможно, так как  и при возрастании номеров
и при возрастании номеров  последовательность
последовательность 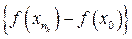 является бесконечно большой. Получили противоречие. Значит, функция
является бесконечно большой. Получили противоречие. Значит, функция  ограничена сверху на отрезке
ограничена сверху на отрезке 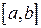 .
.
Аналогично доказывают ограниченность функции  снизу на отрезке
снизу на отрезке 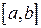 . Следовательно, функция
. Следовательно, функция  ограничена на этом отрезке.
ограничена на этом отрезке. 
Замечание 5.6. Непрерывная функция, заданная на полуинтервале или интервале может не быть ограниченной. Например, функция 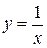 непрерывна на
непрерывна на  , но не является ограниченной сверху на этом промежутке (рис. 5.8), так как
, но не является ограниченной сверху на этом промежутке (рис. 5.8), так как
 .
.
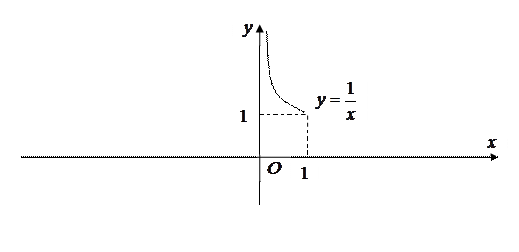
Рис. 5.8. График функции к замечанию 5.6
Свойство II. Наибольшее и наименьшее значения непрерывной функции
Пусть функция 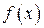 задана на отрезке
задана на отрезке 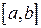 и
и 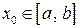 .
.
Определение 5.5. Если для всех точек  выполняется неравенство
выполняется неравенство 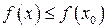 , то говорят, что функция
, то говорят, что функция 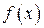 принимает в точке
принимает в точке  наибольшее значение на отрезке
наибольшее значение на отрезке 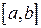 .
.
Если для всех точек  выполняется неравенство
выполняется неравенство 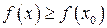 , то говорят, что функция
, то говорят, что функция 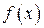 принимает в точке
принимает в точке  наименьшее значение на отрезке
наименьшее значение на отрезке 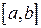 .
.
ТЕОРЕМА 5.3. (Вторая теорема Вейерштрасса). Если функция  непрерывна на отрезке
непрерывна на отрезке 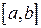 , то хотя бы в одной точке этого отрезка функция принимает наибольшее значение и хотя бы в одной — наименьшее.
, то хотя бы в одной точке этого отрезка функция принимает наибольшее значение и хотя бы в одной — наименьшее.
Замечание 5.7. Требование в теореме 5.3 непрерывности функции  на
на 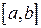 существенно. Функция
существенно. Функция  (пример 2.4) на отрезке
(пример 2.4) на отрезке 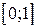 не принимает наибольшее значение, так как на правом конце этого отрезка функция терпит разрыв первого рода, и
не принимает наибольшее значение, так как на правом конце этого отрезка функция терпит разрыв первого рода, и 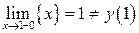 (рис. 5.9).
(рис. 5.9).
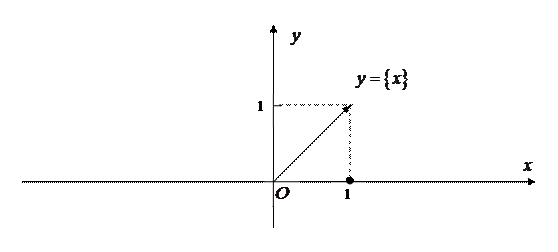
Рис. 5.9. График к замечанию 5.7
Замечание 5.8. Требование непрерывности функции  именно на отрезке существенно. Так функция
именно на отрезке существенно. Так функция 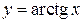 непрерывна и ограничена на всей числовой оси, но не достигает на этом множестве своих наибольшего и наименьшего значений (рис. 2.25).
непрерывна и ограничена на всей числовой оси, но не достигает на этом множестве своих наибольшего и наименьшего значений (рис. 2.25).
Замечание 5.9. Если на множестве 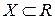 функция
функция  принимает свои наибольшее
принимает свои наибольшее  и наименьшее
и наименьшее 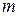 значения, то обозначается это следующим образом:
значения, то обозначается это следующим образом:
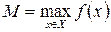 ,
, 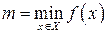 .
.
Свойство III. Теоремы о промежуточных значениях непрерывных функций
ТЕОРЕМА 5.4 (Первая теорема Больцано-Коши о существовании корней непрерывной функции). Пусть функция  определена и непрерывна на отрезке
определена и непрерывна на отрезке 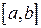 . Тогда, если она принимает на концах отрезка разные по знаку значения, то есть
. Тогда, если она принимает на концах отрезка разные по знаку значения, то есть 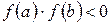 , то существует точка
, то существует точка 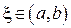 , такая что
, такая что
 .
.
Доказательство. Пусть, для определенности, 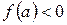 ,
, 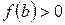 (рис. 5.10). Обозначим отрезок
(рис. 5.10). Обозначим отрезок 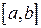 через
через 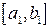 . Разделим этот отрезок пополам точкой
. Разделим этот отрезок пополам точкой 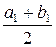 . Тогда в этой точке либо
. Тогда в этой точке либо  обратится в ноль и теорема доказана, либо на одной из половин отрезка знаки функции в концевых точках останутся различными. Выберем эту половину и обозначим её
обратится в ноль и теорема доказана, либо на одной из половин отрезка знаки функции в концевых точках останутся различными. Выберем эту половину и обозначим её 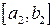 . Далее продолжим процесс деления
. Далее продолжим процесс деления 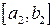 пополам. В точке
пополам. В точке  либо
либо  обратится в ноль, и теорема доказана, либо на одной из половин отрезка
обратится в ноль, и теорема доказана, либо на одной из половин отрезка 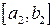 функция на концах будет иметь разные знаки. Обозначим эту половину
функция на концах будет иметь разные знаки. Обозначим эту половину  . В дальнейшем процесс либо прервется, если на одной из середин делимых отрезков получим нулевое значение
. В дальнейшем процесс либо прервется, если на одной из середин делимых отрезков получим нулевое значение  , либо образуется бесконечная последовательность вложенных промежутков
, либо образуется бесконечная последовательность вложенных промежутков  длиной
длиной 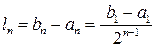 .
.
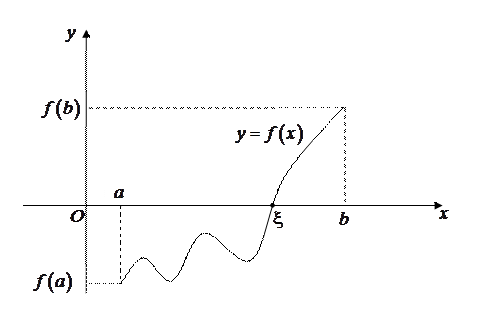
Рис. 5.10. Существование корней непрерывной функции
Тогда  при
при  и по теореме Кантора точки
и по теореме Кантора точки 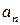 и
и  образуют две сходящиеся к общему пределу последовательности:
образуют две сходящиеся к общему пределу последовательности: 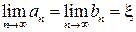 ,
, 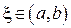 , так как
, так как  и
и  .
.
В соответствии с выбором  и
и 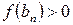
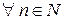 . Отсюда следует, что
. Отсюда следует, что 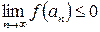 и
и  . С другой стороны, в силу непрерывности
. С другой стороны, в силу непрерывности  и поскольку
и поскольку 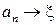 и
и 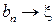 при
при  , то
, то 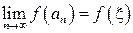 и
и 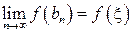 . Значит,
. Значит, 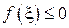 и
и 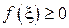 , следовательно,
, следовательно, 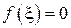 .
. 
ТЕОРЕМА 5.5 (Вторая теорема Больцано-Коши о промежуточных значениях непрерывной функции). Пусть функция  определена и непрерывна на отрезке
определена и непрерывна на отрезке 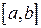 ,
, 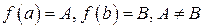 . Тогда для любого числа
. Тогда для любого числа 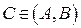 найдется такая точка
найдется такая точка 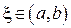 , что
, что 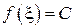 .
.
Доказательство. Рассмотрим функцию 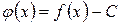 . Она непрерывна на отрезке
. Она непрерывна на отрезке 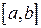 и на концах принимает различные по знаку значения, следовательно, по первой теореме Больцано-Коши существует точка
и на концах принимает различные по знаку значения, следовательно, по первой теореме Больцано-Коши существует точка 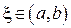 :
: 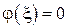 , то есть
, то есть 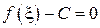 , значит,
, значит, 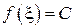 .
. 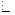
Замечание 5.10. В теоремах 5.4 и 5.5 точка 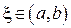 может быть не единственной. На рисунке 5.11 таких точек пять.
может быть не единственной. На рисунке 5.11 таких точек пять.

Рис. 5.11. Промежуточные значения непрерывной функции
Замечание 5.11. В теоремах 5.4 и 5.5 требование непрерывности функции  на отрезке
на отрезке 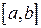 также существенно. Рассмотрим, например, функцию
также существенно. Рассмотрим, например, функцию

Для разрывной функции  не существует
не существует  такой, что
такой, что 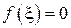 (рис. 5.12).
(рис. 5.12).

Рис. 5.12. График функции к замечанию 5.11
§5.5. Непрерывность сложной и обратной функций.
Непрерывность элементарных функций
|
|
|
|
|
Дата добавления: 2014-12-08; Просмотров: 1980; Нарушение авторских прав?; Мы поможем в написании вашей работы!