Непрерывность обратной функции

ТЕОРЕМА 5.7. Пусть функция 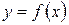, заданная на отрезке 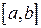с множеством значений 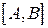есть непрерывная, строго монотонная функция, 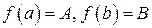, и пусть существует обратная функция 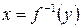с областью определения 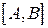и множеством значений 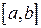. Тогда 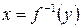непрерывна на отрезке .

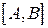Доказательство. Пусть строго возрастает. Убедимся, что 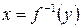строго возрастает на 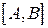(рис. 5.13).

Действительно, если допустить, что при некоторых 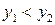выполнено 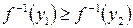, то с учетом строгого возрастания имеем: 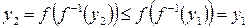, что противоречит условию .

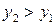Убедимся, что 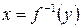непрерывна в любой точке 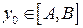. Возьмем произвольную последовательность 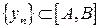, такую что 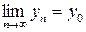. Нужно проверить, что .

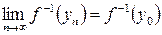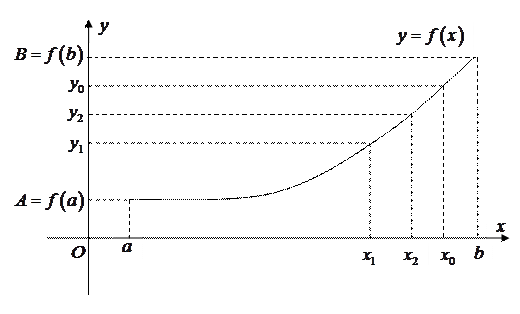
Рис. 5.13

Если это не так, то за пределами некоторой окрестност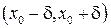и точки 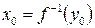содержится бесконечно много членов последовательности 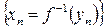. Поэтому можно найти подпоследовательность 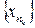: 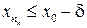(или 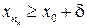). Если, например, выполнено неравенств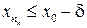о , то .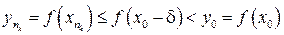

Устремляя 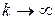, получим 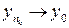(так как 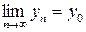, то любая подпоследовательность имеет тот же предел), 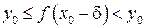, то есть 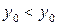. Получаем противоречие. Для убывающей функции доказывается аналогично.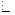

ТЕОРЕМА 5.8 (о существовании обратной функции). Если функция 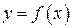непрерывна и строго возрастает (строго убывает) на отрезке 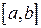, то для неё существует обратная функция 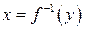непрерывная и строго возрастающая (строго убывающая) на отрезке .

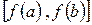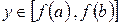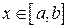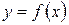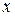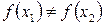Доказательство. Для установления факта наличия обратной функции надо показать, что для любого существует единственная точка такая, что (рис. 5.14). Единственность такой точки вытекает из строгого возрастания функции , согласно которому, при .

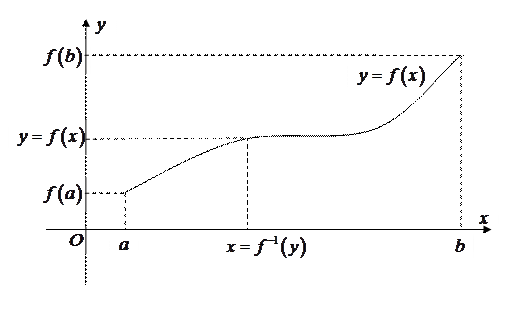
Рис. 5.14. Существование обратной функции

Существование таких точек 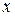, когда 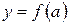и , также очевидно — это точк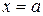и и .

Если же 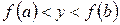, то согласно второй теореме Больцано-Коши, существует точка 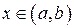, такая что .

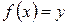Аналогично теорема доказывается для строго убывающей функции.

Дата добавления: 2014-12-08