Точность результатов моделирования

От числа испытаний зависит так же и точность модели. Теория вероятностей позволяет нам оценить эту точность. Относительная величина ошибки приблизительно обратно пропорциональна квадратному корню из числа испытаний. Иными словами, если мы получили N реализаций модели для определения интересующей нас величины Х, то последняя будет получена с ошибкой Dх, наиболее вероятное значение которой определяется из соотношения

.

Например, определяя поток машин в предыдущем примере мы получили х=6, а число реализаций модели составило N=10.Тогда Dх=1,9, что составляет 32%. Это и есть точность нашего результата. х=6+-2.

Мы можем определить число испытаний, для получения ответа с заданной точностью. Нас устроит Dх=1, так как число приезжающих мащин всегда целое число. Оно равно

.

Тогда, для получения необходимой точности число реализаций модели должно составлять N=36.

5.8. Моделирование непрерывной случайной величины

Дискретная случайная величина задается множеством значений и вероятностями того, что случайная величина примет каждое из них. Непрерывная же случайная величина задается законом распределения (функцией плотности вероятности). Для моделирования возможных значений непрерывной случайной величины так же используются случайные числа, имеющие равномерное распределение в интервале [0,1]. Другими словами, случайные числа должны быть преобразованы в возможные значения случайной величины, закон распределения которой задан.

Исходными данными для моделирования являются:

- тип закона распределения случайной величины – функция распределения F(R);

-основные числовые характеристики этого распределения (для нормального закона распределения – дисперсия).

Закон распределения может быть задан не типовой – какой либо приближенной зависимостью приближенного вида. Тогда применяют кусочно-линейную аппроксимацию функции распределения.

Рассмотрим точный методпрямого преобразования случайной величины. Он применяется при задании типовой функции распределения, имеющей аналитическое выражение. Моделирование осуществляется следующим образом:

· Выбирается случайное число R

· По значению случайного числа R и обратной функции распределения вычисляется значение, которое принимает случайная величина.

Например, Случайная величина подчинена показательному закону распределения

С помощью датчика случайных чисел выбираем случайное число R. Тогда

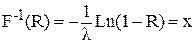
5.9. Примеры построения имитационных моделей

5.9.1. Вычисление числа π с помощью имитационной модели.

Мы рассматривали динамические имитационные модели, в которых осуществлялось моделирование процессов, протекающих во времени. Представленная ниже модель относится к классу статических, не зависящих от времени.

Известно, что число π (отношение длины окружности к диаметру) является иррациональным числом. Оно может быть представлено бесконечной непериодической десятичной дробью π=3,14…. Кроме того, число π трансцендентно, то есть не может быть корнем алгебраического уравнения с целыми коэффициентами. В настоящее время число π вычислено с точностью до триллионного знака. Используются разные методы, например, разложение в ряд. Ряд Лейбница (дает очень медленную сходимость)

Покажем теперь, как можно решить задачу вычисления числа π методом Монте-Карло. Нарисуем квадрат, сторону которого примем за единицу длины. Впишем в этот квадрат четверть круга, как показано на рисунке.

Рис. 26 Схема моделирования числа π

Площадь части круга равна . Площадь квадрата равна единице. Каждая точка R(х,у) внутри рисунка имеет две координаты х и у. Пусть эти координаты являются случайными числами. Если диапазон изменения этих случайных чисел равен [0,1], то любое случайное число R(х,у) будет находиться в площади квадрата. Определим два случайных события, составляющих полную группу:

А – случайное число R попадает в площадь круга с вероятностью Р(А);

В – случайное число R попадает в площадь квадрата, не покрытую кругом с вероятностью Р(В).

Теперь проведем множество реализаций N случайного числа R(х,у). Количество чисел, попавших на поверхность части круга равно n, а вне круга – равно N - n. Очевидно, что отношение площадей равно отношению вероятностей и равно отношению числа попаданий:

. или .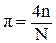

Для того, что бы определить n нам необходимо в этой модели указать условие реализации события А. Естественно, оно будет выглядеть следующим образом. .

Теперь, производя множество реализаций модели и фиксируя результаты, мы можем вычислить число π.Единица соответствует событию А.

Таблица 16

Реализации

Результаты реализаций

Вычислив среднее значение, мы получим π=2,857.

Первый вопрос, который возникает при использовании метода Монте-Карло, связан с количеством испытаний, необходимых для решения задачи с заданной точностью. Ясно, что точность решения повышается с увеличением числа испытаний. Будем использовать приведенную выше формулу:

.

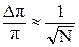Для вычисления числа π мы использовали 14 реализаций и получили значение π=2,857.Этот результат был получен с точностью Dπ = 0,8.

Таким образом, определенное нами число должно быть записано

Dπ =2,857±0,8.Точное значение π=3,14…, как и должно быть, лежит внутри указанного интервала ошибок.

Для получения более точного результата, например с точностью до одной сотой, необходимо провести около ста тысяч реализаций модели .

Дата добавления: 2014-12-16