Матрицы. Операции с матрицами

Библиографический список

1. Акулич И. Л. Математическое программирование в примерах и задачах. – М.: Высшая школа, 1986.

2. Калихман И. Л. Сборник задач по математическому программированию. – М.: Высшая школа, 1975.

3. Курицкий Б. Я. Оптимизация вокруг нас. - Машиностроение, 1989.

4. Таха Х. Введение в исследование операций. – М.: Мир, 1985. Т1, 2.

5. Ногин В. Д. Основы теории оптимизации. – М.: Высш. шк., 1986.

6. Вентцель Е. С. Исследование операций. – М.: Сов. Радио, 1972.

7. Давыдов Е. Г. Исследование операций: Учебное пособ. – М: Высш. шк., 1990.

8. Карманов В. Г. Математическое программирование. – М.: Наука,1986.

9. Федосеев В. В., Гармаш А. Н. Дайитбегов Д. М. и др. Экономико-математические методы и прикладные модели: Учебное пособие для ВУЗов. – М.: ЮНИТИ, 1999.

10. Шелобаев С. И. Матеметические методы и модели в экономике, финансах, бизнесе: Учебное пособие для ВУЗов. - М.: ЮНИТИ-ДАНА, 2000.

11. Кузнецов Математика. - М.: ЮНИТИ-ДАНА, 2004.

Матрицей размера m × n называется упорядоченная таблица, составленная из чисел, расположенных в m строках и n столбцах. Обозначаются матрицы А, В, С и т. д. Элемент матрицы, находящийся в строке с номером i и столбце с номером j, обозначается а_ij. Если m = n, то матрица называется квадратной порядка n.

Произведением матрицы А на число  называется матрица С того же размера, каждый элемент которой равен произведению соответствующего элемента матрицы А на число :

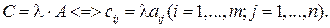
Суммой двух матриц А и В одинаковых размеров называется матрица С того же размера, элементы которой равны сумме соответствующих элементов матриц А и В:

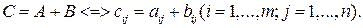
Умножение матрицы А на матрицу В определено, когда число столбцов первой матрицы равно числу строк второй. Тогда произведением матрицы А_{m × k} на матрицу В_{k × n} называется матрица С_{m × n} , каждый элемент которой с_ij равен сумме произведений элементов i -й строки матрицы А на соответствующие элементы j -го столбца матрицы В:

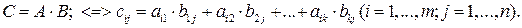
Возведение квадратной матрицы А в целую положительную степень p (p >1):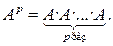

Матрицей, транспонированной к матрице А, называется матрица, образованная из матрицы А заменой её строк соответствующими столбцами. Транспонированная матрица к матрице А обозначается А ^Т.

Всякой квадратной матрице А порядка n ставится в соответствие
по определённому закону некоторое число, которое называется определителем того же порядка матрицы A и обозначается  А .

Определитель первого порядка равен самому числу.

Определитель второго порядка определяется равенством:

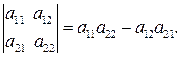(1)

Определителем третьего порядка называется число, которое вычисляется по формуле:

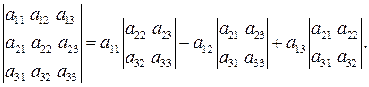(2)

Минором элемента a_ij определителя n -го порядка называется определитель (n –1)-го порядка, полученный из исходного определителя путём вычеркивания i -й строки и j -го столбца. Обозначается минор М_ij.

Алгебраическим дополнением элемента a_ij определителя называется его минор, умноженный на (–1) ^i+j, т. е. А _ij:

А _ij = (–1) ^i+j · М_ij,

где А _ij — алгебраическое дополнение элемента а_{ij .}

Формулу (2) можно записать таким образом:

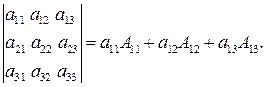
Единичной называется квадратная матрица порядка n, у которой элементы главной диагонали а ₁₁, а ₂₂, …, а_nn равны 1, а остальные элементы равны 0. Пусть Е — единичная матрица. При умножении матрицы А на Е слева или справа получается матрица А: АЕ = ЕА = А.

Матрица А ^–1 называется обратной к квадратной матрице А, если выполняются условия: А·А ^–1 = А ^–1· А = Е.

Обратная матрица к квадратной матрице А существует тогда и только тогда, когда определитель матрицы А не равен нулю, т. е. 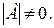При этом

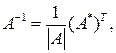(3)

где А ^* — матрица, в которой каждый элемент матрицы А заменён его алгебраическим дополнением. Такая матрица называется присоединённой
к матрице А.

Пример 1. Дана матрица 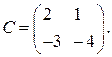Найти матрицу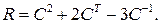

Решение. Определим матрицу С ²:

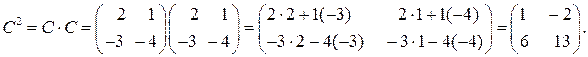
Транспонируем матрицу С: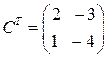

и найдём произведение 2 С^Т: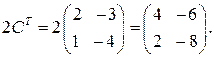

Определим С ^–1 по формуле (3):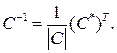

Вычислим определитель матрицы С:

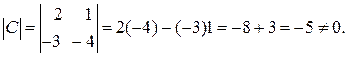
Следовательно, С ^–1 существует. Определим алгебраические дополнения элементов матрицы С и присоединённую матрицу С ^*:

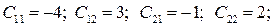
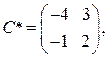тогда 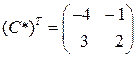и обратная матрица С ^–1: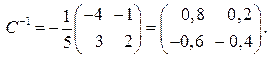

Проверим правильность нахождения С ^–1. Для этого перемножим полученную матрицу на данную матрицу С слева и справа и убедимся, что получается единичная матрица:

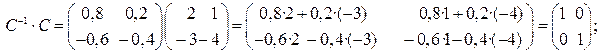
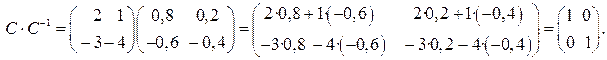Матрица С ^–1 определена правильно.

Найдем произведение матрицы С ^–1 на 3:

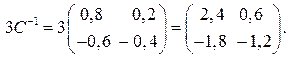
Окончательно получим:

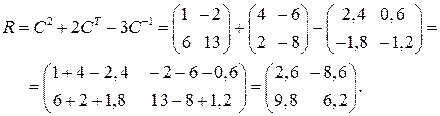
Системы линейных алгебраических уравнений (СЛАУ)

Минором порядка k матрицы А называется определитель порядка k матрицы, составленный из элементов матрицы А, стоящих на пересечении произвольных k строк и k столбцов.

Рангом матрица называется число r, такое, что выполняются условия:

1) существует минор порядка r, не равный нулю;

2) все миноры большего порядка, начиная с (r +1), равны нулю.

Ранг матрицы А обозначается r (А). Ранг матрицы — это наибольший порядок её минора, не равного нулю. Этот минор называется базисным.

Элементарные преобразования, не меняющие ранга матрицы:

1) перестановка строк (столбцов) местами;

2) транспонирование;

3) вычёркивание строки (столбца), все элементы которой равны нулю;

4) умножение какой-либо строки (столбца) на число, отличное от нуля;

5) прибавление к элементам одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число.

Рассмотрим систему m уравнений с n неизвестными:

(4)

Обозначим матрицу из коэффициентов при неизвестных:

её называют основной матрицей системы.  

,

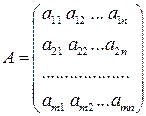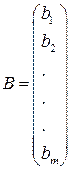— столбец свободных членов, — столбец неизвестных,

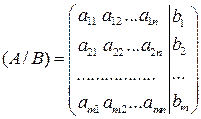— расширенная матрица системы.

Систему уравнений (4) можно записать в матричном виде:

А·Х = В. (4^/)

Совокупность чисел d ₁, d ₂,…, d_n, обращающих все уравнения системы (4) в тождества, называется решением системы.

Система уравнений совместна, если она имеет хотя бы одно решение, и несовместна, если она не имеет решения.

Две системы уравнений называются равносильными, если множества их решений совпадают.

Элементарные преобразования системы уравнений, переводящие
её в равносильную систему:

1) перестановка местами любых двух уравнений;

2) умножение обеих частей любого уравнения на число, отличное
от нуля;

3) прибавление к обеим частям одного уравнения соответствующих частей другого, умноженных на одно и то же число.

Система уравнений называется неоднородной, если 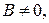и однородной, если В = 0.

Система уравнений называется определённой, если она имеет единственное решение, и неопределённой, если она имеет бесконечное множество решений.

Исследование системы уравнений на совместность основано на следующей теореме:

Теорема Кронекера—Капелли. Для того, чтобы система уравнений
с n неизвестными была совместна, необходимо и достаточно чтобы ранг матрицы системы был равен рангу расширенной матрицы системы,
т. е. r (А) = r (А  В) = r.

При этом:

1) если r = n, система определена;

2) если r < n, система не определена.

Рассмотрим следующие методы решения СЛАУ: метод Крамера, матричный метод, метод Жордана—Гаусса.

Дата добавления: 2014-12-16