Краткие сведения из теории пределов функции

Решение.

а) Используя правила I, III и формулу (3), получим:

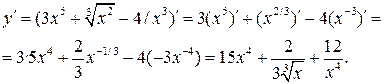
б) Используя правила дифференцирования произведения функций II, разности I, формулы (5), (7), (8) и учитывая, что независимая переменная есть t, т. е. t =1, получим:

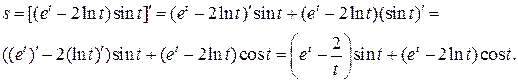
в) Сложная степенная функция, независимая переменная есть v,
т. е. v =1; используя формулу (3), получим:

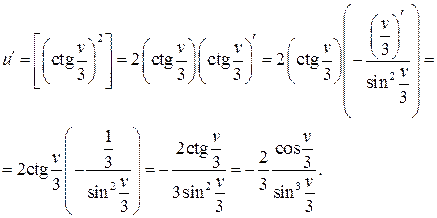
г) Используя правила дифференцирования частного IV, суммы I, III
и формулы (3), (14), учитывая, что t =1, получим:

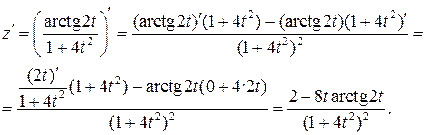
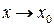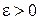Число А называют пределом функции f (x) при (и пишут ), если для любого найдется число 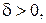зависящее от , такое, что для всех 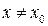, удовлетворяющих условию 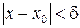, выполняется неравенство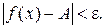

Функция (x) называется бесконечно малой (б.м.ф.) пр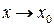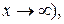и ( если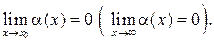

Функция f (x) называется бесконечно большой (б.б.ф.) при 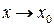, ( 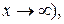если для любого M >0 найдётся число 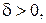зависящее от М, такое, что для всех 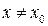, удовлетворяющих условию 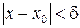, будет верно неравенство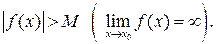

Если (x) есть б. м.ф. пр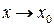и (или 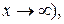то функция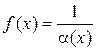

является б. б., и обратно, если f (x) б.б.ф. при 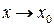, то 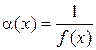является б.м.ф.

Есл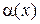и и 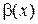б.м.ф. при 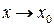(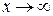), то чтобы сравнить их, нужно вычислить предел их отношения. Пусть 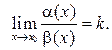Тогда:

при 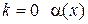называется б.м. более высокого порядка малости, чем ;

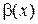пр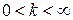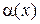и и 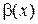одного порядка малости;

при 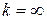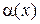более низкого порядка малости, чем .

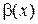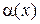Если , то б.м.ф. и 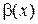называются эквивалентными: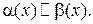

Предел отношения двух б.м.ф. не изменится, если каждую б.м.ф. заменить на эквивалентную.

Примеры эквивалентных б.м.ф. при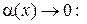

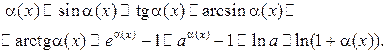
Теоремы о пределах:

1. 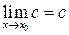(c =const).

2. Если 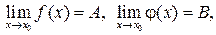то:

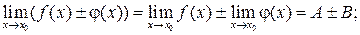
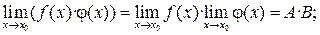
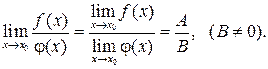
Первый замечательный предел: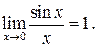

Второй замечательный предел (число е = 2,718…):

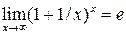или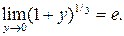

Чтобы найти предел элементарной функции 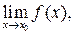нужно предельное значение аргумента подставить в функцию и посчитать. При этом, если х = х ₀ принадлежит области определения функции, то значение предела будет найдено, оно равно значению функции в точке х = х ₀. При вычислении пределов полезно использовать следующие соотношения. Если то, учитывая свойства б.б. и б.м. функций, получим:

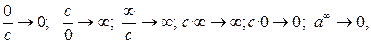если 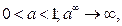если a >1.

Случаи, в которых подстановка предельного значения аргумента
в функцию не дает значения предела, называют неопределенностями;
к ним относятся неопределенности видов:

Устранить неопределенность можно с помощью алгебраических преобразований или используя правило Лопиталя.

Правило Лопиталя. Предел отношения двух б.м. 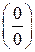или б.б. 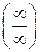функций равен пределу отношения их производных (конечному или бесконечному), если последний существует:

(5)

Чтобы использовать правило Лопиталя для раскрытия неопределённостей других типов, выражение под знаком предела следует преобразовать элементарными способами так, чтобы получить неопределенность 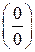или 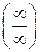и затем использовать формулу (5).

Пример 4. Найти пределы, используя правило Лопиталя или элементарные способы раскрытия неопределённостей:

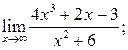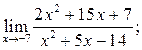а) б) в)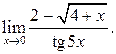

Дата добавления: 2014-12-16