Метод Гаусса

Матричный метод

Метод Крамера

Применяется для решения неоднородных систем n уравнений с n
неизвестными, у которых определитель основной матрицы системы отличен от нуля: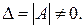

Тогда система имеет единственное решение:

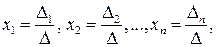(5)

где  _i — определитель, полученный из определителя системы  заменой
i -го столбца матрицы А столбцом свободных членов В.

Применяется при тех же условиях, что и метод Крамера. Столбец неизвестных находим, решая матричное уравнение (4). Умножим (4) слева на матрицу А ^–1:

А ^–1· А · Х = А ^–1· В.

По определению обратной матрицы А ^–1· А = Е, следовательно,

Е·Х = А ^–1· В.

Умножение матрицы на единичную матрицу не меняет матрицу, поэтому Е·Х = Х и

Х = А ^–1· В. (6)

Применяется для решения как неоднородных, так и однородных систем с произвольным числом уравнений m и произвольным числом неизвестных n. С помощью элементарных преобразований строк расширенной матрицы системы (А  В) исходную систему (4) преобразуют в равносильную, которая позволяет решить вопрос о совместности системы, и, если она совместна, записать её решение. Преобразования проводятся так, чтобы матрица (А  В) приобрела треугольный вид (элементы, расположенные ниже главной диагонали равны), после чего, если, система совместна, находят её решение или делают вывод о её несовместности.

Замечание 1. Если при преобразованиях появляется строка, полностью состоящая из нулей, то её можно отбросить.

Замечание 2. Если при преобразованиях появляется строка, соответствующая противоречивому уравнению вида:

0· х ₁+ 0· х ₂ + … + 0· х_n = b_i, где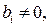

то процесс преобразований на этом прекращают, так как система уравнений несовместна.

Пример 2. Дана система уравнений А·Х = В, где

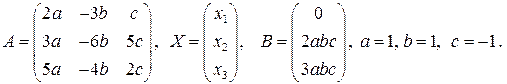
Решить систему тремя методами:

а) по формулам Крамера;

б) матричным методом;

в) методом Жордана—Гаусса.

Решение. Согласно условиям задания имеем:

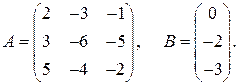
Систему линейных алгебраических уравнений А·Х = В запишем в координатной форме:

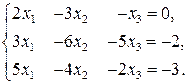
а) Решим систему по формулам Крамера.

Найдём определитель системы, используя формулы (2) и (1):

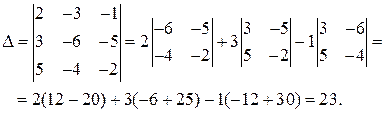
Так как 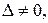система имеет единственное решение, которое находим по формулам Крамера (5):

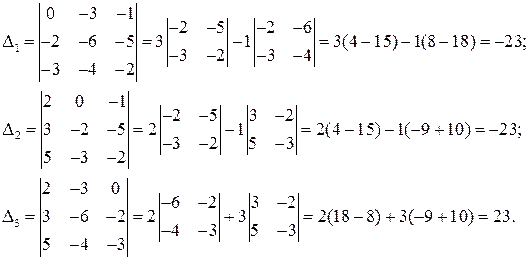
Итак,

Сделаем проверку, подставив найденные значения х ₁, х ₂, х ₃ в исходную систему, и убедимся, что все три уравнения данной системы обращаются в тождества:

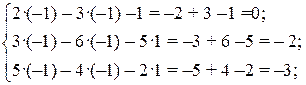
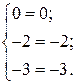
Ответ: х ₁ = –1, х ₂ = –1, х ₃ =1.

б) Решим систему матричным методом.

Из пункта а) 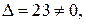следовательно, матрица системы имеет обратную А ^–1, которую найдём по формуле (3).

Для этого вычислим алгебраические дополнения:

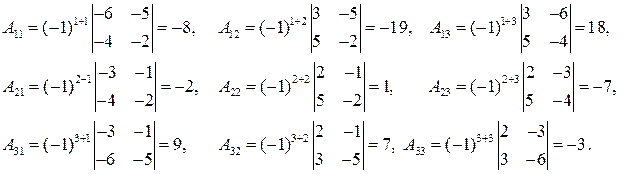Получим А ^–1 по формуле (3):

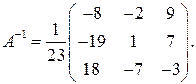
По формуле (6) имеем

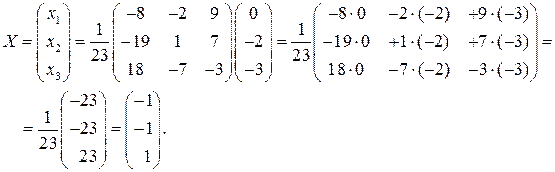
Ответ: х ₁ = –1, х ₂ = –1, х ₃ = 1.

в) Решим систему методом Гаусса.

Преобразования расширенной матрицы системы оформим в виде таблицы (см. табл.).

А/В		Примечания
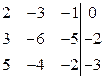
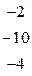
		Вычтем из второй строки первую и поменяем эти строки местами.

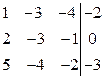
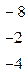
		Вычтем из второй строки первую, умноженную на 2, а из третьей строки первую, умноженную на 5.
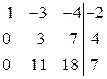
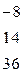
		Вычтем из третьей строки вторую, умноженную на 4, и поменяем знаки элементов полученной третьей на противоположные.
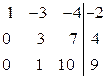
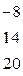
		Поменяем вторую и третью строку местами.
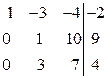
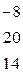
		Вычтем из третьей строки вторую, умноженную на 3.
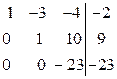
		Разделим третью строку на (-23).
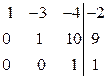
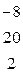
		Преобразования закончены. Очевидно, что ранги матриц А, и А  В совпадают и равны 3, следовательно система совместна и имеет единственное решение.

Замечание. Во втором столбце таблицы для контроля записаны суммы строк матрицы А  В, с которыми производим те же преобразования, что и с элементами матрицы, если на каком-то шаге преобразований элемент второго столбца не будет равен сумме элементов соответствующей строки матрицы А  В, то допущена ошибка при преобразовании данной строки.

Итак, найдём решение системы. Система уравнений после преобразований перешла в равносильную ей систему:

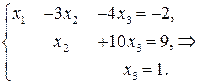
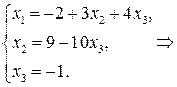
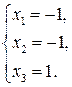
Отметим, что решения системы, полученные в пунктах а), б) и в), как и следовало ожидать, совпадают.

Ответ: х ₁ = –1, х ₂ = –1, х ₃ = 1.

Производная функции и её приложения

Производной функции 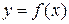называется конечный предел отношения приращения функции 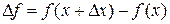к приращению независимой переменной 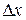при стремлении последнего к нулю:

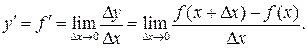(1)

Обозначения производной в точке х ₀:

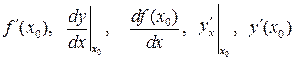и другие.

Если функция в точке х ₀ (или на промежутке Х) имеет конечную производную, то функция называется дифференцируемой в этой точке (или на промежутке Х).

Процесс отыскания производной называется дифференцированием.

Дата добавления: 2014-12-16