
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Неопределенный интеграл. Непосредственное интегрирование
|
|
|
|
Решение.
а) Подставляя в функцию вместо х предельное значение  , определим предел числителя и знаменателя.
, определим предел числителя и знаменателя.
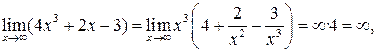 т. к.
т. к. 
Аналогично: 
Имеем неопределенность вида 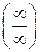 . Используем правило Лопиталя:
. Используем правило Лопиталя:
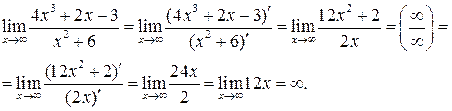
б) 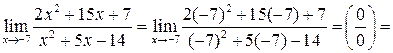
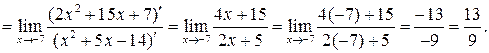
в) 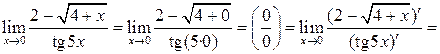

Замечание. Если, применив правило Лопиталя, снова получили неопределенность 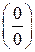 или
или 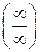 , то снова применяем правило до тех пор, пока неопределённость не будет раскрыта.
, то снова применяем правило до тех пор, пока неопределённость не будет раскрыта.
Функция 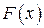 , определенная на интервале
, определенная на интервале  , называется первообразной для функции
, называется первообразной для функции 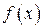 , определенной на том же интервале
, определенной на том же интервале  , если
, если 
Если 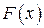 — первообразная для функции
— первообразная для функции 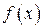 , то любая другая первообразная
, то любая другая первообразная  для функции
для функции 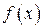 отличается от
отличается от 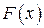 на некоторое постоянное слагаемое, т. е.
на некоторое постоянное слагаемое, т. е.  где
где 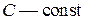 .
.
Неопределенным интегралом от функции 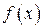 называется совокупность всех первообразных для этой функции. Обозначается неопределенный интеграл:
называется совокупность всех первообразных для этой функции. Обозначается неопределенный интеграл: 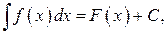 где
где 
Операция нахождений первообразной для данной функции называется интегрированием. Интегрирование является обратной операцией к дифференцированию:

Для проверки правильности выполненного интегрирования необходимо продифференцировать результат интегрирования и сравнить полученную функцию с подынтегральной.
Свойства неопределенного интеграла:
1. 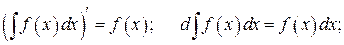
2. 
3. 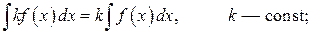
4. 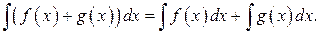
Таблица основных интегралов
1.  2.
2. 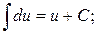
3. 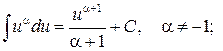
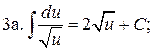
4.  5.
5. 
6.  7.
7. 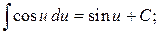
8.  9.
9. 
10.  11.
11. 
12.  13.
13. 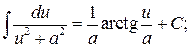
14.  15.
15. 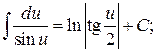
16. 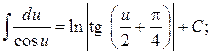 17.
17. 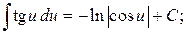
18. 
Каждая из приведенных в таблице формул справедлива на промежутке, не содержащем точек разрыва подынтегральной функции. Вычисление интегралов с использованием таблицы и основных свойств называют непосредственным интегрированием.
Пример 5. Пользуясь таблицей основных интегралов и свойствами неопределенного интеграла, найти интегралы 

|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 667; Нарушение авторских прав?; Мы поможем в написании вашей работы!