Ответ: 0,840

Ответ: 0,757

Ответ: 0,6910

Ответ: 0,1972

Ответ: 0,9544

Ответ: 0,6828

Ответ: 0,1359

Ответ: 0,9544

в) в интервале (12; 14), если М(Х) = 10, s(Х) = 2.

г) в интервале (15; 25), если М(Х) = 20, s(Х) = 5.

д) в интервале (13; 18), если М(Х) = 3, s(Х) = 4.

е) в интервале (0; 4), если М(Х) = 2, s(Х) = 1.

ж) в интервале (5; 10), если М(Х) = 8, D(Х) = 9.

з) в интервале (-1,6; 1,6), если М(Х) = 1,2, s(Х) = 0,8.

и) в интервале (-10; 10), если М(Х) = -3, D(Х) = 64.

к) в интервале (0; 4), если М(Х) = 3, s(Х) = 1.

12. Случайная величина Х распределена нормально с математическим ожиданием 10 и средним квадратическим отклонением s = 5. Найти интервал, симметричный относительно математического ожидания, в который с вероятностью 0,9973 попадёт величина Х в результате испытания.

Ответ: (-5; 25).

13. Среднее квадратическое отклонение нормально распределённой случайной величины Х равно 5 мм. Найти длину интервала, симметричного относительно математического ожидания, в который с вероятностью 0,9973 попадёт Х в результате испытания.

Ответ: b = 30 мм.

14. Случайная величина Х распределена нормально с математическим ожиданием равным 8 и средним квадратическим отклонением s = 0,8. Найти интервал, в который с вероятностью 0,999 попадёт Х в результате испытания.

Ответ: (5,6; 10,4).

15. Найти интервал, в который с вероятностью 0,998 попадёт нормально распределённая величина Х, если её М(Х) = 10, s = 8,7.

Ответ: (11, 19).

16. Найти интервал, в который с вероятностью 0,9975 попадёт нормально распределённая величина Х, если её М(Х) = 15, s = 1.

Ответ: (12, 18).

17. Случайная величина Х распределена нормально с математическим ожиданием 12 и средним квадратическим отклонением s = 5. Найти интервал, в который с вероятностью 0,9973 попадёт Х в результате испытания.

Ответ: (-3; 27).

18. Среднее квадратическое отклонение нормально распределённой случайной величины равно 12 мм. Найти длину интервала, в который с вероятностью 0,9975 попадёт в результате испытания величина Х.

Ответ: 6 s = 72 мм.

19. Станок автомат изготовляет валики, причём контролируется их диаметр Х. Считая, что случайная величина Х нормально распределена с математическим ожиданием 10 и средним квадратическим отклонением s = 0,1. Найти интервал, в который с вероятностью 0,9981 будут заключены диаметры валиков.

Ответ: (9,7; 10,3)

20. Автомат штампует детали. Контролируется длина детали Х, которая распределена нормально с математическим ожиданием (проектная длина), равным 50 мм. Фактическая длина изготовленной детали не менее 32 мм и не более 68 мм. Найти вероятность того,что длина наудачу взятой детали:

а) больше 55 мм;

б) меньше 40 мм.

Ответ: а) Р (55 < X < 68) = 0,0822; б) Р (32 < X < 40) = 0.026.

21. Вероятность выигрыша по облигации займа за все время его действия равна 0,1. Составить закон распределения числа выигравших облигаций среди приобретенных 19. Найти математическое ожидание, дисперсию, среднеквадратическое отклонение и моду этой случайной величины.

22. По данным примера 21 найти математическое ожидание, дисперсию, среднеквадратическое отклонение доли (частоты) выигравших облигаций среди приобретенных.

23. Составить функцию распределения случайной величины, имеющей биноминальный закон распределения с параметрами п и р.

24. Устройство состоит из 1000 элементов, работающих независимо один от другого. Вероятность отказа любого элемента в течение времени t равна 0,002. Необходимо: а) составить закон распределения отказавших за время t элементов; б) найти математическое ожидание и дисперсию этой случайной величины; в) определить вероятность того, что за время t откажет хотя бы один элемент.

25. Вероятность поражения цели равна 0,05. Производится стрельба по цели до первого попадания. Необходимо: а) составить закон распределения сделанных выстрелов; б) найти математическое ожидание и дисперсию этой случайной величины; в) определить вероятность того, что для поражения цели потребуется не менее 5 выстрелов.

26. В магазине имеются 20 телевизоров, из них 7 имеют дефекты. Необходимо: а) составить закон распределения числа телевизоров с дефектами среди выбранных наудачу пяти; б) найти математическое ожидание и дисперсию этой случайной величины; в) определить вероятность того, что среди выбранных нет телевизоров с дефектами.

27. Цена деления шкалы измерительного прибора равна 0,2. Показания прибора округляются до ближайшего целого числа. Полагая, что при отсчете ошибка округления распределена по равномерному закону, найти: 1) математическое ожидание, дисперсию и среднее квадратическое отклонение этой случайной величины; 2) вероятность того, что ошибка округления: а) меньше 0,04; б) больше 0,05.

28. Среднее время безотказной работы прибора равно 80 ч. Полагая, что время безотказной работы прибора имеет показательный закон распределения, найти: а) выражение его плотности вероятности и функции распределения; б) вероятность того, что в течение 100 ч прибор не выйдет из строя.

29. Текущая цена акции может быть смоделирована с помощью нормального закона распределения с математическим ожиданием 15 ден. ед.

1) Найти вероятность того, что цена акции: а) не выше 15,3 ден. ед.; б) не ниже 15,4 ден. ед.; в) от 14,9 до 15,3 ден. ед.

2) С помощью правила трех сигм найти границы, в которых будет находиться текущая цена акции.

30. Цена некой ценной бумаги нормально распределена. В течение последнего года 20 % рабочих дней она была ниже 88 ден. ед., а 75 % выше 90 ден. ед. Найти: а) математическое ожидание и среднее квадратическое отклонение цены ценной бумаги; б) вероятность того, что в день покупки цена будет заключена в пределах от 83 до 96 ден. ед.; в) с надежностью 0,95 определить максимальное отклонение цены ценной бумаги от среднего (прогнозного) значения (по абсолютной величине).

31. Коробки с конфетами упаковываются автоматически. Их средняя масса равна 540 г. Известно, что 5 % коробок имеют массу, меньшую 500 г. Каков процент коробок, масса которых: а) менее 470 г; б) от 500 до 550 г; в) более 550 г; г) отличается от средней не более, чем на 30 г (по абсолютной величине)?

32. Случайная величина Х имеет следующую функцию распределения: F(x) = 0,5 + 0,5 Ф(х – 1). Из какого интервала (1; 2) или (2; 6) она примет значение с большей вероятностью?

33. Квантиль уровня 0,15 нормально распределенной случайной величины Х равен 12, а квантиль уровня 0,6 равен 16. Найти математическое ожидание и среднее квадратическое отклонение случайной величины.

34. 20-ти процентная точка нормально распределенной случайной величины равна 50, а 40 процентная точка равна 35. Найти вероятность того, что случайная величина примет значение в интервале (25; 45).

35. Месячный доход семей можно рассматривать как случайную величину, распределенную по логнормальному закону. Полагая, что математическое ожидание этой случайной величины равно 1000 ден. ед., а среднее квадратическое отклонение 800 ден. ед., найти долю семей, имеющих доход: а) не менее 1000 ден. ед.; б)менее 500 ден. ед.

36. Среднее изменение курса акций компании в течение одних биржевых торгов составляет 0,3 %. Оценить вероятность того, что на ближайших торгах курс изменится более чем на 3 %.

37. Отделение банка обслуживает в среднем 100 клиентов в день. Оценить вероятность того, что сегодня в отделении банка будет обслужено: а) не более 200 клиентов; б) более 150.

38. Электростанция обслуживает сеть на 1600 электроламп, вероятность включения каждой из которых вечером равна 0,9. Оценить с помощью неравенства Чебышева вероятность того, что число ламп, включенных в сеть вечером, отличается от своего математического ожидания не более, чем на 100 (по абсолютной величине). Найти вероятность того же события, используя следствие из интегральной теоремы Муавра-Лапласа.

39. Вероятность того, что акции, переданные на депозит, будут востребованы, равна 0,08. Оценить с помощью неравенства Чебышева вероятность того, что среди 1000 клиентов от 70 до 90 востребуют свои акции.

40. Среднее значение длины детали 50 см, а дисперсия 0,1. Используя неравенство Чебышева, оценить вероятность того, что случайно взятая деталь окажется по длине не менее 49,5 и не более 50,5 см. Уточнить вероятность того же события, если известно, что длина случайно взятой детали имеет нормальный закон распределения.

41. Оценить вероятность того, что отклонение любой случайной величины от ее математического ожидания будет не более двух средних квадратических отклонений (по абсолютной величине).

42. В течение времени t эксплуатируются 500 приборов. Каждый прибор имеет надежность 0,98 и выходит из строя независимо от других. Оценить с помощью неравенства Чебышева вероятность того, что доля надежных приборов отличается от 0,98 не более чем на 0,1 (по абсолютной величине).

43. Вероятность сдачи в срок всех экзаменов студентом факультета равна 0,7. С помощью неравенства Чебышева оценить вероятность того, что доля сдавших в срок все экзамены из 2 000 студентов заключена в границах от 0,66 до 0,74.

44. Бензоколонка N заправляет легковые и грузовые автомобили. Вероятность того, что проезжающий легковой автомобиль подъедет на заправку, равна 0,3. С помощью неравенства Чебышева найти границы, в которых с вероятностью, не меньшей 0,79, находится доля заправившихся в течение 2 ч легковых автомобилей, если за это время всего заправилось 100 автомобилей.

45. В среднем 10% работоспособного населения некоторого региона – безработные. Оценить с помощью неравенства Чебышева вероятность того, что уровень безработицы среди обследованных 10000 работоспособных жителей города будет в пределах от 9% до 11% (включительно).

46. Опыт работы страховой компании показывает, что страховой случай приходится примерно на каждый пятый договор. Оценить с помощью неравенства Чебышева необходимое количество договоров, которые следует заключить, чтобы с вероятностью 0,9 можно было утверждать, что доля страховых случаев отклонится от 0,1 не более чем на 0,01 (по абсолютной величине). Уточнить ответ с помощью следствия из интегральной теоремы Муавра – Лапласа.

47. В целях контроля из партии в 100 ящиков взяли по одной детали из каждого ящика и измерили их длину. Требуется оценить вероятность того, что вычисленная по данным выборки средняя длина детали отличается от средней длины детали во всей партии не более чем на 0,3 мм, если известно, что среднее квадратическое отклонение не превышает 0,8 мм.

ПРИЛОЖЕНИЯ

Приложение 1

Таблица значений локальной функции Лапласа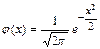

х		0,01	0,02	0,03	0,04	0,05	0,06	0,07	0,08	0,09
	0,3989	0,3989	0,3989	0,3988	0,3986	0,3984	0,3982	0,3980	0,3977	0,3973
0,1	0,3970	0,3965	0,3961	0,3956	0,3951	0,3945	0,3939	0,3932	0,3925	0,3918
0,2	0,3910	0,3902	0,3894	0,3885	0,3876	0,3867	0,3857	0,3847	0,3836	0,3825
0,3	0,3814	0,3802	0,3790	0,3778	0,3765	0,3752	0,3739	0,3725	0,3712	0,3697
0,4	0,3683	0,3668	0,3653	0,3637	0,3621	0,3605	0,3589	0,3572	0,3555	0,3538
0,5	0,3521	0,3503	0,3485	0,3467	0,3448	0,3429	0,3410	0,3391	0,3372	0,3352
0,6	0,3332	0,3312	0,3292	0,3271	0,3251	0,3230	0,3209	0,3187	0,3166	0,3144
0,7	0,3123	0,3101	0,3079	0,3056	0,3034	0,3011	0,2989	0,2966	0,2943	0,2920
0,8	0,2897	0,2874	0,2850	0,2827	0,2803	0,2780	0,2756	0,2732	0,2709	0,2685
0,9	0,2661	0,2637	0,2613	0,2589	0,2565	0,2541	0,2516	0,2492	0,2468	0,2444
	0,2420	0,2396	0,2371	0,2347	0,2323	0,2299	0,2275	0,2251	0,2227	0,2203
1,1	0,2179	0,2155	0,2131	0,2107	0,2083	0,2059	0,2036	0,2012	0,1989	0,1965
1,2	0,1942	0,1919	0,1895	0,1872	0,1849	0,1826	0,1804	0,1781	0,1758	0,1736
1,3	0,1714	0,1691	0,1669	0,1647	0,1626	0,1604	0,1582	0,1561	0,1539	0,1518
1,4	0,1497	0,1476	0,1456	0,1435	0,1415	0,1394	0,1374	0,1354	0,1334	0,1315
1,5	0,1295	0,1276	0,1257	0,1238	0,1219	0,1200	0,1182	0,1163	0,1145	0,1127
1,6	0,1109	0,1092	0,1074	0,1057	0,1040	0,1023	0,1006	0,0989	0,0973	0,0957
1,7	0,0940	0,0925	0,0909	0,0893	0,0878	0,0863	0,0848	0,0833	0,0818	0,0804
1,8	0,0790	0,0775	0,0761	0,0748	0,0734	0,0721	0,0707	0,0694	0,0681	0,0669
1,9	0,0656	0,0644	0,0632	0,0620	0,0608	0,0596	0,0584	0,0573	0,0562	0,0551
	0,0540	0,0529	0,0519	0,0508	0,0498	0,0488	0,0478	0,0468	0,0459	0,0449
2,1	0,0440	0,0431	0,0422	0,0413	0,0404	0,0396	0,0387	0,0379	0,0371	0,0363
2,2	0,0355	0,0347	0,0339	0,0332	0,0325	0,0317	0,0310	0,0303	0,0297	0,0290
2,3	0,0283	0,0277	0,0270	0,0264	0,0258	0,0252	0,0246	0,0241	0,0235	0,0229
2,4	0,0224	0,0219	0,0213	0,0208	0,0203	0,0198	0,0194	0,0189	0,0184	0,0180
2,5	0,0175	0,0171	0,0167	0,0163	0,0158	0,0154	0,0151	0,0147	0,0143	0,0139
2,6	0,0136	0,0132	0,0129	0,0126	0,0122	0,0119	0,0116	0,0113	0,0110	0,0107
2,7	0,0104	0,0101	0,0099	0,0096	0,0093	0,0091	0,0088	0,0086	0,0084	0,0081
2,8	0,0079	0,0077	0,0075	0,0073	0,0071	0,0069	0,0067	0,0065	0,0063	0,0061
2,9	0,0060	0,0058	0,0056	0,0055	0,0053	0,0051	0,0050	0,0048	0,0047	0,0046
	0,0044	0,0043	0,0042	0,0040	0,0039	0,0038	0,0037	0,0036	0,0035	0,0034

Приложение 2

Таблица значений интегральной функции Лапласа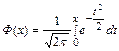

х		0,01	0,02	0,03	0,04	0,05	0,06	0,07	0,08	0,09
	0,0000	0,0040	0,0080	0,0120	0,0160	0,0199	0,0239	0,0279	0,0319	0,0359
0,1	0,0398	0,0438	0,0478	0,0517	0,0557	0,0596	0,0636	0,0675	0,0714	0,0753
0,2	0,0793	0,0832	0,0871	0,0910	0,0948	0,0987	0,1026	0,01064	0,1103	0,1141
0,3	0,1179	0,1217	0,1255	0,1293	0,1331	0,1368	0,1406	0,1443	0,1480	0,1517
0,4	0,1554	0,1591	0,1628	0,1664	0,1700	0,1736	0,1772	0,1808	0,1844	0,1879
0,5	0,1915	0,1950	0,1985	0,2019	0,2054	0,2088	0,2123	0,2157	0,2190	0,2224
0,6	0,2257	0,2291	0,2324	0,2357	0,2389	0,2422	0,2454	0,2486	0,2517	0,2549
0,7	0,2580	0,2611	0,2642	0,2673	0,2704	0,2734	0,2764	0,2794	0,2823	0,2852
0,8	0,2881	0,2910	0,2939	0,2967	0,2995	0,3023	0,3051	0,3078	0,3106	0,3133
0,9	0,3159	0,3186	0,3212	0,3238	0,3264	0,3289	0,3315	0,3340	0,3365	0,3389
	0,3413	0,3438	0,3461	0,3485	0,3508	0,3531	0,3554	0,3577	0,3599	0,3621
1,1	0,3643	0,3665	0,3686	0,3708	0,3729	0,3749	0,3770	0,3790	0,3810	0,3830
1,2	0,3849	0,3869	0,3888	0,3907	0,3925	0,3944	0,3962	0,3980	0,3997	0,4015
1,3	0,4032	0,4049	0,4066	0,4082	0,4099	0,4115	0,4131	0,4147	0,4162	0,4177
1,4	0,4192	0,4207	0,4222	0,4236	0,4251	0,4265	0,4279	0,4292	0,4306	0,4319
1,5	0,4332	0,4345	0,4357	0,4270	0,4382	0,4394	0,4406	0,4418	0,4429	0,4441
1,6	0,4452	0,4463	0,4474	0,4484	0,4495	0,4505	0,4515	0,4525	0,4535	0,4545
1,7	0,4554	0,4564	0,4573	0,4582	0,4591	0,4599	0,4608	0,4616	0,4625	0,4633
1,8	0,4641	0,4649	0,4656	0,4664	0,4671	0,4678	0,4686	0,4693	0,4699	0,4706
1,9	0,4713	0,4719	0,4726	0,4732	0,4738	0,4744	0,4750	0,4756	0,4761	0,4767
	0,4772	0,4778	0,4783	0,4788	0,4793	0,4798	0,4803	0,4808	0,4812	0,4817
2,1	0,4821	0,4826	0,4830	0,4834	0,4839	0,4842	0,4846	0,4850	0,4854	0,4857
2,2	0,4861	0,4864	0,4868	0,4871	0,4875	0,4878	0,4881	0,4884	0,4887	0,4890
2,3	0,4893	0,4896	0,4898	0,4901	0,4904	0,4906	0,4909	0,4911	0,4913	0,4916
2,4	0,4918	0,4920	0,4922	0,4925	0,4927	0,4929	0,4931	0,4932	0,4934	0,4936
2,5	0,4938	0,4940	0,4941	0,4943	0,4945	0,4946	0,4948	0,4949	0,4951	0,4952
2,6	0,4953	0,4955	0,4956	0,4957	0,4959	0,4960	0,4961	0,4962	0,4963	0,4964
2,7	0,4965	0,4966	0,4967	0,4968	0,4969	0,4970	0,4971	0,4972	0,4973	0,4974
2,8	0,4974	0,4975	0,4976	0,4977	0,4977	0,4978	0,4979	0,4979	0,4980	0,4981
2,9	0,4981	0,4982	0,4982	0,4983	0,4984	0,4984	0,4985	0,4985	0,4986	0,4986
	0,4987	0,4987	0,4987	0,4988	0,4988	0,4989	0,4989	0,4989	0,4990	0,4990

Приложение 3

Таблица значений функции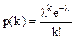

k\l	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9
	0,9048	0,8187	0,7408	0,6703	0,6065	0,5488	0,4966	0,4493	0,4066
	0,0905	0,1637	0,2222	0,2681	0,3033	0,3293	0,3476	0,3595	0,3659
	0,0045	0,0164	0,0333	0,0536	0,0758	0,0988	0,1217	0,1438	0,1647
	0,0002	0,0011	0,0033	0,0072	0,0126	0,0198	0,0284	0,0383	0,0494
		0,0000	0,0003	0,0007	0,0016	0,0030	0,0050	0,0077	0,0111
				0,0000	0,0002	0,0004	0,0007	0,0012	0,0020
							0,0000	0,0002	0,0003
k\l
	0,3679	0,1353	0,0498	0,0183	0,0067	0,0025	0,0009	0,0003	0,0001	0,0000
	0,3679	0,2707	0,1494	0,0733	0,0337	0,0149	0,0064	0,0027	0,0011	0,0005
	0,1839	0,2707	0,2240	0,1465	0,0842	0,0446	0,0223	0,0107	0,0050	0,0023
	0,0613	0,1804	0,2240	0,1954	0,1404	0,0892	0,0521	0,0286	0,0150	0,0076
	0,0153	0,0902	0,1680	0,1954	0,1755	0,1339	0,0912	0,0573	0,0337	0,0189
	0,0031	0,0361	0,1008	0,1563	0,1755	0,1606	0,1277	0,0916	0,0607	0,0378
	0,0005	0,0120	0,0504	0,1042	0,1462	0,1606	0,1490	0,1221	0,0911	0,0631
		0,0034	0,0216	0,0595	0,1044	0,1377	0,1490	0,1396	0,1171	0,0901
		0,0009	0,0081	0,0298	0,0653	0,1033	0,1304	0,1396	0,1318	0,1126
		0,0002	0,0027	0,0132	0,0363	0,0688	0,1014	0,1241	0,1318	0,1251
			0,0008	0,0053	0,0181	0,0413	0,0710	0,0993	0,1186	0,1251
			0,0002	0,0019	0,0082	0,0225	0,0452	0,0722	0,0970	0,1137
				0,0006	0,0034	0,0113	0,0263	0,0481	0,0728	0,0948
				0,0002	0,0013	0,0052	0,0142	0,0296	0,0504	0,0729
					0,0005	0,0022	0,0071	0,0169	0,0324	0,0521
					0,0002	0,0009	0,0033	0,0090	0,0194	0,0347
						0,0003	0,0014	0,0045	0,0109	0,0217
						0,0001	0,0006	0,0021	0,0058	0,0128
							0,0002	0,0009	0,0029	0,0071
								0,0004	0,0014	0,0037
								0,0002	0,0006	0,0019

ЛИТЕРАТУРА

1. Афанасьева О.Н., Бродский Я.С., Павлов А.Л. Математика для техникумов на базе среднего образования: Учебное пособие. – М.: Издательство физико-математической литературы, 2005. – 464 с.

2. Гмурман В. Е. Теория вероятностей и математическая статистики: Учебное пособие для вузов М.: Высшая школа, 1999. – 480с.

3. Гмурман В. Е. Руководство по решению задач по теории вероятностей и математической статистики. - М.: Высшая школа, 1999. – 400с.

4. Пехлецкий И.Д. Математика. – М.: Издательский центр «Академия», 2003. – 304 с.

5. Письменный Д.Т. Конспект лекций по теории вероятностей, математической статистике и случайным процессам. – М.: Айрис-Пресс, 2008. – 288с.

ОГЛАВЛЕНИЕ

	Введение
	Классическое определение вероятности. Геометрическая вероятность.
	Вероятность произведения и суммы событий и появления хотя бы одного события
	Формула полной вероятности. Формула Байеса. Повторение испытаний. Формулы Берну-лли, Муавра-Лапласа и Пуассона. Наивероятнейшее число успехов
	Дискретные и непрерывные случайные величины. Ряд распределения. Интегральная и дифференциальная функция распределения
	Числовые характеристики случайных величин
	Нормальный закон распределения
	Приложения
	Литература

Составитель: Елена Васильевна Морозова

Светлана Васильевна Мягкова

Дата добавления: 2014-11-29