Условие пересечения двух плоскостей и угол между ними

ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ДВУХ ПЛОСКОСТЕЙ

Пусть относительно декартовой прямоугольной системы координат x, y, z две плоскости заданы своими общими уравнениями

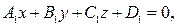(3.12)

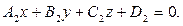(3.13)

Рассмотрим условия различного расположения таких плоскостей.

Теорема. Для того, чтобы плоскости, заданные уравнениями (3.12) и (3.13) в декартовой прямоугольной системе координат, пересекались, необходимо и достаточно, чтобы соответствующие коэффициенты при x, y, z в уравнениях (3.12) и (3.13) не были пропорциональны или чтобы хотя бы один из определителей

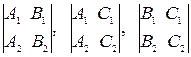(3.14)

был отличен от нуля.

Доказательство. Необходимым и достаточным условием пересечения двух плоскостей является неколлинеарность их нормальных векторов 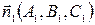и 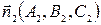. Вектора же 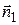и 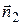неколлинеарны тогда и только тогда, когда непропорциональны их соответствующие координаты (кн.2, гл.4, §3, п.3.3), т.е. когда хотя бы один из определителей (3.14) отличен от нуля. Например,

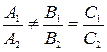означает, что ;

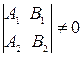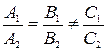означает, что .

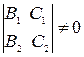Найдем угол между пересекающимися плоскостями. Под этим углом мы будем понимать один из смежных двугранных углов, образованных этими плоскостями.

Пусть угол между данными плоскостями φ. Тогда угол между нормальными векторами этих плоскосте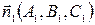й и 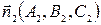также будет равен φ или 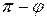. Угол φ найдем по формуле скалярного произведения двух векторов 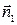и :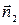

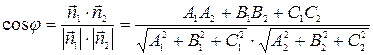. (3.15)

Положив в этой формуле 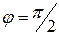, получим условие перпендикулярности плоскостей:

.

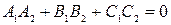Дата добавления: 2014-11-29