Расстояние от точки до плоскости

ПРИВЕДЕНИЕ ОБЩЕГО УРАВНЕНИЯ ПЛОСКОСТИ К НОРМАЛЬНОМУ ВИДУ

Пусть дано общее уравнение плоскости

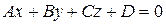. (3.21)

Умножим обе части этого уравнения на число :

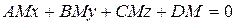. (3.22)

Уравнение (3.22) будет приведено к нормальному виду, если выполняются условия (3.20):

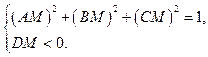
Решая эту систему относительно М, получаем

,

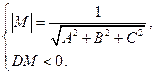Число М называется нормирующим множителем уравнения (3.21).

Если 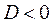, то 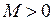, и тогда

.

Если 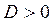, 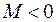и тогда

.

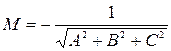Таким образом, знак нормирующего множителя противоположен знаку свободного члена уравнения плоскости. Если 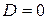, то М можно взять с любым знаком.

Итак, чтобы преобразовать общее уравнение плоскости в нормальное, нужно обе части общего уравнения умножить на его нормирующий множитель.

Теорема. Если плоскость задана нормальным уравнением

,

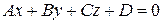(где 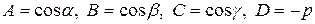) относительно декартовой прямоугольной системы координат, то расстояние d от точки 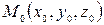до этой плоскости вычисляется по формуле

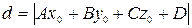(или ),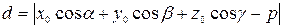

т.е. расстояние от точки до плоскости, заданной нормальным уравнением относительно декартовой прямоугольной системы координат, равно абсолютной величине результата подстановки координат данной точки в левую часть уравнения плоскости.

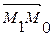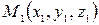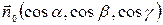Доказательство. Из точки М ₀ на данную плоскость опустим перпендикуляр и рассмотрим вектор , где точка – основание перпендикуляра, принадлежит плоскости. Тогда (рис.3.6). Вектора и 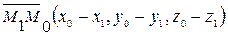коллинеарны, поэтому, учитывая, что 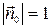, имеем

.

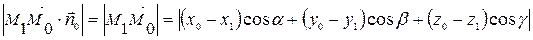Отсюда, принимая во внимание, что (точка М ₁ принадлежит плоскости), получаем

.

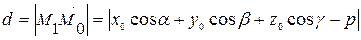Если плоскость задана общим уравнением

,

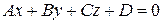то для того, чтобы найти расстояние d от точки 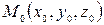до плоскости, нужно сначала привести уравнение к нормальному виду, а затем найти абсолютное значение его левой части в точке М ₀:

.

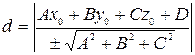Замечание. Иногда расстоянию от точки до плоскости приписывают знак; называют такое расстояние отклонением и полагают

,

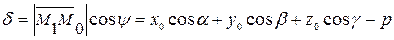где 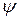– угол между коллинеарными векторами и .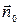

Плоскость делит пространство на два полупространства. Для точек, находящихся в полупространстве, содержащем начало координат О (0, 0, 0) 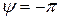и 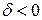. Это полупространство называют отрицательным. Для полупространства, не содержащего начало координат, 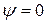и (рис.3.6). Это полупространство называют положительным.

ГЛАВА 4

Дата добавления: 2014-11-29