Длина вектора

Координаты вектора

Три взаимно перпендикулярные оси X, Y, Z (рис.1.9) образуют декартову прямоугольную систему координат. Имеется две системы прямоугольных координат — правая и левая.

Для правой системы координат поворот оси X на 90⁰ до совмещения ее с осью Y виден со стороны оси Z против часовой стрелки, а для левой — по часовой.

Прямоугольными координатами вектора 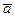называются проекции вектора 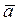на оси координат (рис. 1.9). Координаты вектора обозначаются буквами a_x,a_y, a_z.

Запись:

. (1.3)

Векторы 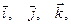изображенные на рисунке, называются единичными ортами (единичными векторами) координатных осей. Их модули равны единице, а направления совпадают с направлением осей OX, OY и OZ. Зная проекции вектора 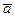, можно представить его как

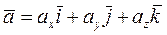(1.4)

Длина вектора = {с_x,с_y, с_z} выражается через его координаты по теореме Пифагора формулой

. (1.5)

После определения , являющегося суммой векторов 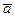и 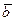, часто возникает задача нахождения модуля вектора , т. е. его длины. Возможны следующие случаи:

1. Складываемые векторы сонаправлены (). В этом случае от векторной записи

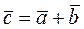(1.6)

легко перейти к скалярной, спроектировав уравнение (1.6) на ось OX (рис.1.10), параллельной векторам

OX: . (1.7)

2. Складываемые векторы противоположно направлены . Спроектировав уравнение

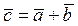
на ось OX (рис. 1.11), получаем

OX: . (1.8)

3. Складываемые векторы перпендикулярны (рис. 1.12). Модуль вектора находим по теореме Пифагора, записанной для прямоугольного треугольника ODE. 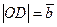и 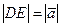- катеты треугольника, 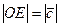- его гипотенуза. Поэтому

. (1.9)

4. Угол 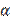между складываемыми векторами произвольный (рис. 1.13) (α не равен 0°, 90°, 180°, как это имело место выше). В этом случае применяется теорема косинусов: Квадрат одной стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение сторон на косинус угла между ними. Для треугольника ODE, в котором известны стороны, и 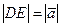а также угол α, теорема запишется как

(1.10)

Применяя теорему косинусов, следует помнить, что в ней идет речь не об угле между складываемыми векторами и (угле β), а об угле

α = 180° - β. Так как cos (180° - β) = -cosβ, выражение (1.10) можно записать в следующем виде:

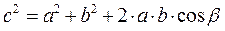. (1.10а)

Дата добавления: 2014-11-29