
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Примеры решения задач. Углы между осями координат и вектором
|
|
|
|
Углы между осями координат и вектором
Углы α,β,γ образуемые положительными направлениями OX, OY, OZ с вектором 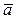 = {ax ay az} (рис. 1.14), можно
= {ax ay az} (рис. 1.14), можно  найти по формулам
найти по формулам
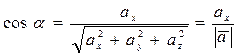 , (1.11)
, (1.11)
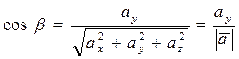 , (1.12)
, (1.12)

 .
.
|
Задача 1.1
Самолет держит курс на север со скоростью  = 200м/с относительно Земли. Дует западный ветер со скоростью относительно Земли
= 200м/с относительно Земли. Дует западный ветер со скоростью относительно Земли 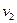 = 15 м/с. Найти скорость самолета v относительно воздуха.
= 15 м/с. Найти скорость самолета v относительно воздуха.
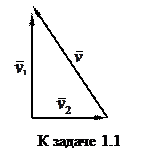 Дано:
Дано:  = 200 м/с;
= 200 м/с; 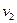 = 15 м/с.
= 15 м/с.
Найти: v.
Решение Скорость самолета относительно воздуха 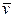 равна
равна 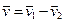 . Изобразим треугольник скоростей (рис. З 1.1).
. Изобразим треугольник скоростей (рис. З 1.1).
Так как 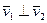 , модуль искомой скорости находим по теореме Пифагора:
, модуль искомой скорости находим по теореме Пифагора:
 =200,56м/с.
=200,56м/с.
Ответ: скорость самолета относительно воздуха
v = 200,56м/с.
Задача 1.2
К телу приложены силы 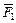 и
и 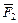 , угол между которыми
, угол между которыми 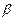 = 20°. Найти модуль результирующей силы
= 20°. Найти модуль результирующей силы 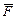 , действующей на тело, если
, действующей на тело, если 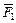 =
= 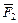 = 20Н.
= 20Н.
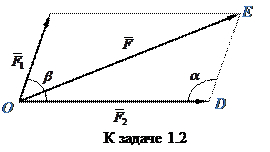 Дано:
Дано: 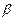 = 20°;
= 20°; 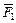 = 20 Н;
= 20 Н; 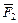 = 20Н.
= 20Н.
Найти: F.
Решение. Результирующая сила 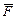 , действующая на тело, — это векторная сумма сил
, действующая на тело, — это векторная сумма сил 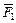 и
и 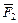 :
: 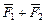 (рис. З 1.2). Найдем сумму векторов
(рис. З 1.2). Найдем сумму векторов 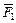 и
и 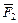 по правилу параллелограмма. Для треугольника сил ОДЕ (ОД =
по правилу параллелограмма. Для треугольника сил ОДЕ (ОД = 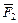 , ДЕ =
, ДЕ = 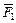 , ОЕ =
, ОЕ = 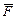 ) запишем теорему косинусов в виде:
) запишем теорему косинусов в виде:
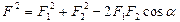 , где α =180° -
, где α =180° - 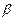 .
.
Так как по условию 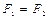 то
то
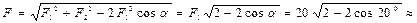 39.4Н.
39.4Н.
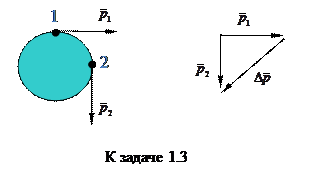
Ответ модуль результирующей силы F 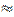 39,4 Н.
39,4 Н.
 Задача 1.3
Задача 1.3
Тело массой m = 1кг движется с постоянной по модулю скоростью v = 10м/с по окружности. Найти модуль изменения импульса тела 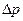 при прохождении четверти окружности (импульсом называется произведение массы тела m на его скорость
при прохождении четверти окружности (импульсом называется произведение массы тела m на его скорость 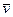 ).
).
Дано: v = 10 м/с; m = 1кг.
Найти: 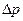 .
.
Решение. Изменение какой-либо величины - это разность конечной и начальной величины. Значит, 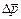 =
= 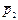 -
- 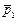 . Пусть тело находилось в точке 1 и, двигаясь по часовой стрелке, оказалось в точке 2. Так как импульс по определению есть
. Пусть тело находилось в точке 1 и, двигаясь по часовой стрелке, оказалось в точке 2. Так как импульс по определению есть 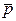 = m
= m 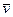 , то векторы
, то векторы 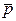 и
и 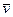 сонаправлены. Вектор скорости
сонаправлены. Вектор скорости 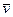 , направлен по касательной к траектории тела. Поэтому в точке 1 вектор
, направлен по касательной к траектории тела. Поэтому в точке 1 вектор  , горизонтален, а в точке 2 вектор
, горизонтален, а в точке 2 вектор  вертикален. Построим разность векторов
вертикален. Построим разность векторов 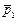 и
и  (рис. З 1.2). Тик как
(рис. З 1.2). Тик как 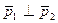 , то по теореме Пифагора
, то по теореме Пифагора
|
 .
.
|
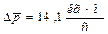 .
.
Задача 1.4
Вектор скорости тела меняется со временем по закону 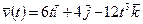 , м/с, где t - время, а
, м/с, где t - время, а 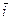 ,
, 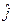 ,
, 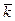 — орты координатных осей. Найти зависимость модуля скорости от времени v (t).
— орты координатных осей. Найти зависимость модуля скорости от времени v (t).
Дано: 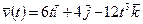 , м/с.
, м/с.
Найти: v (t).
Решение. В данной задаче вектор 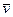 выражен через проекции на координатные оси и орты
выражен через проекции на координатные оси и орты 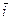 ,
, 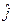 ,
, 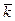 координатных осей (см. с. 16). Сомножители при ортах
координатных осей (см. с. 16). Сомножители при ортах 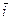 ,
, 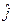 ,
, 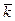 - это проекции вектора скорости на оси OX, OY, OZ, соответственно. Таким образом,
- это проекции вектора скорости на оси OX, OY, OZ, соответственно. Таким образом, 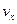 = 6 t м/с,
= 6 t м/с, 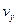 = 4м/с,
= 4м/с, 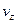 = -12
= -12 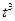 м/с. Тогда модуль вектора скорости
м/с. Тогда модуль вектора скорости
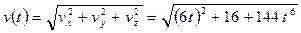 , м/с.
, м/с.
Ответ: зависимость модуля скорости от времени 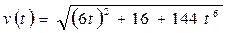 ,м/с.
,м/с.
Задача 1.5
Найти угол αмежду силой  , Н, действующей на тело, и осью ОХ в момент времени t = 1с.
, Н, действующей на тело, и осью ОХ в момент времени t = 1с.
Дано: 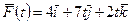 ,H; t = 1 с.
,H; t = 1 с.
Найти:α.
Решение. Найдем длину вектора  . Как и в предыдущей задаче, запишем компоненты вектора
. Как и в предыдущей задаче, запишем компоненты вектора  :
:
Fx= 4 Н, Fy = 7tН, FZ= 2t Н.
Используя формулу (1.11), получаем
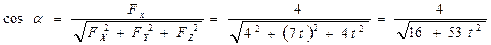 .
.
В данную формулу подставим значение времени t = 1 с:
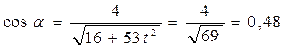 ,
, 
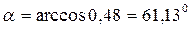 .
.
Ответ: между силой  и осью ОX угол
и осью ОX угол  .
.
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 5527; Нарушение авторских прав?; Мы поможем в написании вашей работы!