Расчет входящего потока требований

ТЕХНОЛОГИЧЕСКИЙ РАСЧЕТ СИСТЕМЫ ТО И ТР, ОРГАНИЗОВАННОЙ ИЗ УНИВЕРСАЛЬНЫХ ПОСТОВ, С УЧЕТОМ СЛУЧАЙНОСТИ СОБЫТИЙ, ПРОИСХОДЯЩИХ В СИСТЕМЕ

ЧАСТЬ 2

В первой части была рассмотрена методика расчета системы обслуживания и ремонта автомобилей дорожной СТО, построенная на использовании средних значений основных характеристик работы системы и на целом ряде произвольно подбираемых расчетных и поправочных коэффициентов.

Во второй части настоящих методических указаний поставлена задача познакомить студентов с новым подходом к проектированию зон ТО и ТР с позиций системного анализа и с учетом случайности событий, происходящих в системе обслуживания и ремонта автомобилей.

Решение поставленной задачи основывается на использовании ряда основных положений теории массового обслуживания.

Использование для этих целей теории массового обслуживания и вероятностных методов исследования позволяет создать относительно простую математическую модель для проведения сопоставленной оценки эффективности принимаемых решений в части выбора оптимального числа рабочих постов.

Анализ производственной деятельности СТО, в том числе и дорожных, показывает, что, как правило, в их систему ТО и ТР поступает поток требований со случайными отказами, требующими для своего устранения технических воздействий случайной продолжительности.

Вполне естественно, что поток случайных отказов формирует и случайный поток обслуживаний.

Таким образом, процесс поступления в систему обслуживания и ремонта потока требований является вероятностным.

В дальнейшем будем считать, что в результате ряда допущений и наложения определенных условий на входящий поток он отвечает требованиям стационарности, ординарности и отсутствия последействия, а проектируемая система ТО и ТР относится к системам с ожиданием требований без потерь.

При установившемся (стационарном) процессе обслуживания и ремонте автомобилей поступающий в систему, поток требований является пауссоновским простейшим, в котором вероятность поступления в промежуток времени (0, t) К требований определяется выражением:

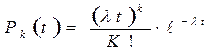, (2.1)

где 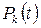– вероятность поступления К требований за время (0,t);

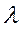– плотность потока требований (среднее число требований,

поступающих за единицу времени).

Величина математического ожидания числа требований, поступающих в систему, равна:

.

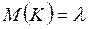При 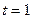выражение (1) принимает вид:

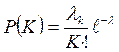(2.2)

Из выражения (2.2) следует, что для полного списания простейшего потока требований на обслуживание или ремонт достаточно знать параметр плотности потока требований: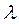

Согласно закону больших чисел при большом числе появлений требований на обслуживание или ремонт значение величины 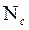(среднесуточного количества автомобилей, требующих обслуживания) приближается к ее математическому ожиданию:

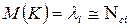(2.3)

Таким образом, для того чтобы описать поток и иметь его характеристику, достаточно определить величину .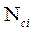

Дисперсия случайной величины К, распределенной по закону Пауссона, равна ее математическому ожиданию 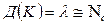. Следовательно, величина среднеквадратичного отклонения случайной величины К равна .

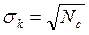Таким образом, плотность потока требований, поступающих в систему, колеблется в пределах:

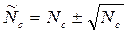(2.4)

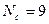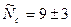Например, если , то или 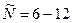, т.е. поток изменяется в два раза.

Для этого потока требуется соответствующая организация работ в зонах обслуживания и ремонта и достаточная для этого производственная мощность.

Дата добавления: 2014-11-29