Случайные величины и законы распределения

Схема независимых испытаний

(схема Бернулли).

Определение: Если при проведении нескольких испытаний вероятность события А в каждом испытании не зависит от исходов других событий, то эти испытания называются независимыми относительно события А.

Определение: Пусть проводится сложное испытание, состоящее из серии n одинаковых, независимых относительно А испытаний, причем каждое составляющее испытание имеет два исхода: появление события А – успех; непоявление события А – неуспех. Вероятность успеха во всех испытаниях одинакова и равна p. Вероятность неуспеха равна q = 1-p. В этом случае говорят, что испытание проводится по схеме Бернулли.

Поставим задачу: Вычислить вероятность Р_n (k) того, что при n испытаниях событие А осуществится ровно k раз. Не требуется, чтобы событие А появилось k раз в определенной последовательности.

Вероятность одного сложного события «в n испытаниях событие А наступит k раз и не наступит (n - k) раз» по теореме умножения вероятностей независимых событий равна .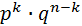

Таких сложных событий может быть столько, сколько можно составить сочетаний из n элементов по k элементов, т.е. 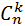(т.к. успехи появляются в любом порядке). Эти сложные события несовместны, следовательно, по теореме сложения вероятностей несовместных событий искомая вероятность 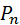(k) равна сумме вероятностей всех возможных сложных событий, а т.к. их вероятности равны 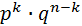, то справедлива формула:

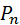(k) = ,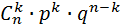

где 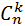– количество сложных событий,

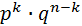– вероятность сложного события.

Эта формула называется формулой Бернулли.

Пример: Вероятность того, что расход электроэнергии в продолжение одних суток не превысит установленной нормы, равна 0,75. Найти вероятность того, что в ближайшие шесть суток расход электроэнергии в течение любых четырех суток не превысит нормы.

Решение: По формуле Бернулли получаем:

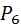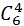
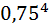
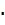
(4) = 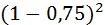= 0,3.

Заметим, что вероятность появления успеха в n испытаниях не менее m раз можно вычислить так:

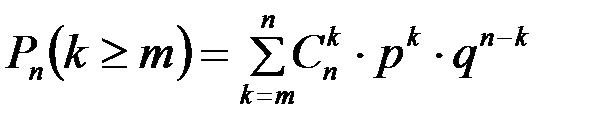
или

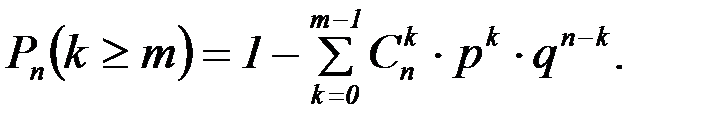
А вероятность появления успеха хотя бы один раз в n испытаниях можно вычислить по формуле:

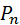(k ≥ 1)= 1 - .

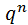Если число испытаний n достаточно велико, то пользоваться формулой Бернулли становится трудно. Следует пользоваться приближенными формулами.

Теорема Муавра - Лапласа (локальная теорема Лапласа): Если вероятность p появления события А в каждом испытании постоянна и отлична от нуля и единицы (0<p<1), то вероятность 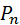(k) того, что событие А появится в n испытаниях ровно k раз, приближенно равна (тем точнее, чем больше n):

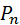(k) (x),

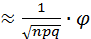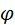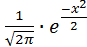где (x) = , x = .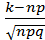

Заметим, что 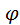(x) – четная функция, т.е. 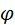(- x) = 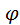(x). Значения этой функции приведены в соответствующей таблице для x 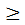0.

Муавр доказал эту теорему для p = , а Лаплас обобщил ее для всех значений вероятности, удовлетворяющих неравенству:

0 < p < 1.

Пример: Вероятность рождения мальчика равна 0,51. Найти вероятность того, что среди 100 новорожденных окажется ровно 50 мальчиков.

Решение: n = 100, k = 50, p = 0,51, q = 0,49.

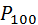(50) ) =

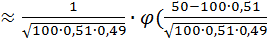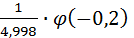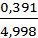= = = 0,0782.

Интегральная теорема Лапласа: Вероятность 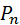( 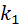, 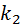) того, что в n независимых испытаниях, в каждом из которых вероятность появления события А равна p (0<p<1), событие А наступит не менее 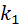раз и не более 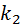раз, приближенно равна:

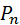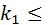( k ) = ( , )

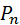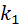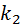где 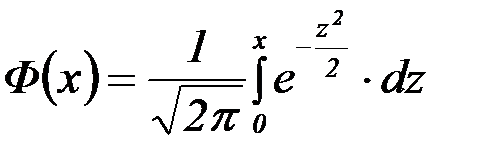– функция Лапласа,

= , = .

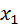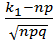Значения функции 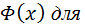x 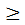0 даны в таблице. 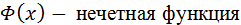, для нее выполняется равенство:

= .

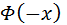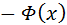Для x >5 = 0,5.

Пример: Вероятность того, что деталь не прошла проверку ОТК, равна p = 0,2. Найти вероятность того, что среди 400 случайно отобранных деталей окажутся непроверенными от 70 до 100 деталей.

Решение: p = 0,2, q = 0,8, n = 40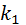0, = 70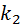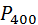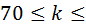, = 100.

( 100) ,

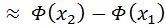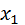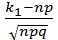= = -1,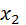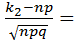25, = 2,5.

Тогда получаем:

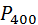( 100)

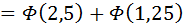= 0,4938 + 0,3944 = 0,8882.

Итак, если испытания проходят по схеме Бернулли, и их количество n велико, то вместо формулы Бернулли используют приближенные формулы Лапласа (асимптотические формулы). Но эти формулы непригодны, если вероятность события мала (p 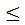0,1).

Таким образом, если n велико, а p мало, пользуются приближенной (асимптотической) формулой Пуассона. Выведем эту формулу для вычисления вероятности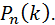

Сделаем важное допущение: произведение np сохраняет постоянное значение, а именно np = .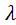

Воспользуемся формулой Бернулли:

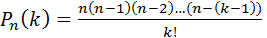
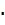
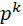
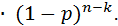
Так как pn = 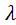, то p = 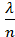, тогда получаем:

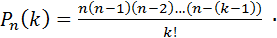
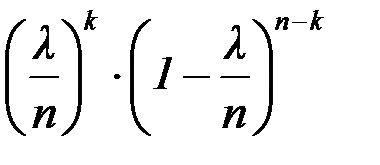
Так как n очень велико, то

Это приближенное равенство, т.к. n хоть и велико, но конечно, а мы устремляем n к бесконечности. Так как np сохраняет постоянное значение, то p при n

Тогда получаем:

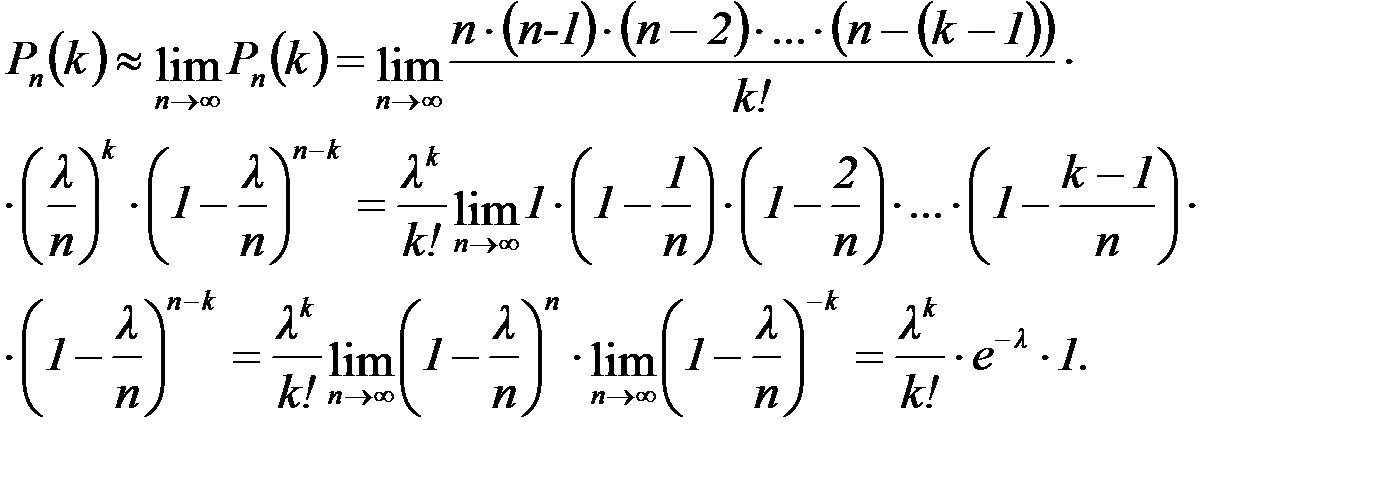
Итак, мы получили формулу Пуассона:

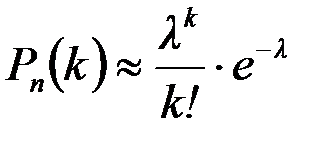
Этой формулой обычно пользуются, если λ < 4, p ≤ 0,1.

Пример: Завод отправил на базу 5000 хрустальных ваз. Вероятность того, что в пути ваза разобьется, равна 0,0002. Найти вероятность того, что в дороге разобьются три вазы.

Решение: n = 5000, p = 0,0002, k = 3.

Дата добавления: 2014-12-27