
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Экспериментов
|
|
|
|
Условные вероятности, независимость событий и
1.11.1. Теоремы умножения вероятностей.
Определение: Условной вероятностью PA(B) (или P(B/A)) называют вероятность события B, вычисленную в предположении, что событие A уже наступило.
Определение: Условной вероятностью P(B/AC) относительно произведения событий A и C называется вероятность наступления события B при условии, что A и C уже наступили.
Пример: В урне 3 белых и 5 чёрных шаров. Из урны вынимают один шар, а затем второй. Первый шар оказался чёрным. Найти вероятность того, что второй шар будет:
а) белым,
b) чёрным.
Решение: а) P(A/B) – второй шар будет белым, при условии, что первый – чёрный:
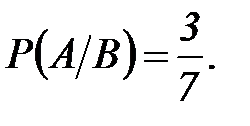
b) P(C/B) – второй шар будет чёрным, при условии, что первый – чёрный:
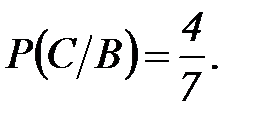
Теорема 1: Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое уже произошло:
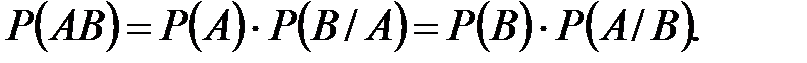
Доказательство: Пусть из n возможных элементарных исходов событию A благоприятствует m исходов, из которых k исходов благоприятствует событию B. Тогда:

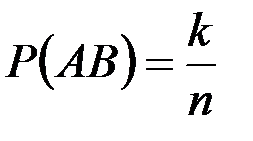 , т.к. событию AB благоприятствуют те исходы, которые одновременно благоприятствуют и событию A, и событию B, т.е. k.
, т.к. событию AB благоприятствуют те исходы, которые одновременно благоприятствуют и событию A, и событию B, т.е. k.

Аналогично доказывается и формула 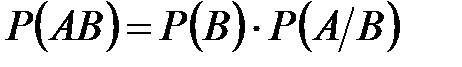
Следствие: Для вероятности большего числа событий справедлива формула:
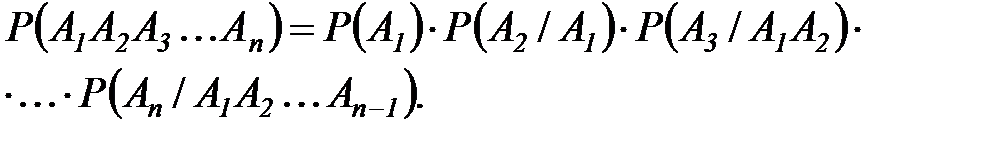
Доказательство проводится методом математической индукции.
Пример: На склад поступило 35 холодильников. Известно, что 5 холодильников с дефектами, но неизвестно, какие именно. Найти вероятность того, что два холодильника, взятых наугад, будут с дефектами.
Решение: Пусть событие A – «первый выбранный холодильник с дефектом», событие B – «второй выбранный холодильник с дефектом». Тогда получаем:

Определение: Если при наступлении события A вероятность события B не меняется, то события A и B называются независимыми.
Пример: Два стрелка стреляют по мишени. Событие A – «первый стрелок попал в мишень», событие B – «второй стрелок попал в мишень (промахнулся)». События A и B – независимые.
Теорема 2: Если события A и B – независимые, то вероятность их произведения равна произведению их вероятностей: 
Доказательство: Так как события A и B независимы, то условная вероятность события А равна его безусловной вероятности:

Тогда по теореме 1 получаем:

Следствие: Если события A1, A2, …, An – независимы, то вероятность их произведения равна произведению их вероятностей:
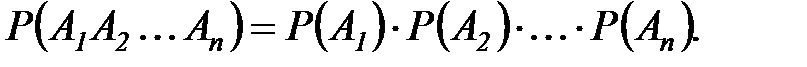
Доказательство проводится методом математической индукции.
Заметим, что если события 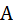 и
и  – независимы, то независимы также события:
– независимы, то независимы также события: 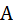 и
и  ,
,  и B,
и B, 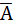 и
и  .
.
Определение: Несколько событий называются независимыми, если независимы каждые два из них и независимы каждое событие и все возможные произведения остальных.
Пример: Найти вероятность появления «орла» при однократном бросании трех монет.
Решение: Пусть событие A1 – «орёл на первой монете», событие A2 – «орёл на второй монете», событие A3 – «орёл на третьей монете».
События A1, A2, A3 – независимые, следовательно:

Теорема 3: Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
P( 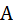 +
+  ) = P(
) = P( 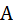 ) + P(
) + P(  B) - P(
B) - P(  ).
).
Доказательство: Событие (A+B) наступит, если наступит одно из трёх несовместных событий:  ,
,  B,
B, 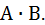
Тогда по теореме о вероятности суммы конечного числа несовместных событий, получаем:
P (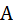 +
+  ) = P (
) = P ( ) + P (
) + P ( B) + P (
B) + P ( ). (1)
). (1)
Событие 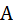 наступит, если наступит одно из двух несовместных событий:
наступит, если наступит одно из двух несовместных событий:  или
или  . Тогда имеем:
. Тогда имеем:
P (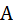 ) = P (
) = P ( ) + P (
) + P ( ),
),
P ( ) = P (
) = P (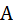 ) - P (
) - P ( ).
).
Аналогично, получаем:
P (B) = P ( B) + P (
B) + P ( ),
),
P ( B) = P (B) - P (
B) = P (B) - P ( ).
).
Подставим эти результаты в формулу (1) и получим:
P (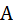 +
+  ) = P (
) = P (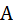 ) + P (
) + P ( B) - P (
B) - P ( ).
).
Пример: Если вероятность поступления в магазин одного вида товара Р(А)=0,4, а второго вида товара – Р(В)=0,5, и если допустить, что эти события независимы, но совместны, то вероятность суммы событий равна:
Р(А+В)= 0,4 + 0,5 - 0,4 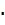 0,5 = 0,7.
0,5 = 0,7.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 1054; Нарушение авторских прав?; Мы поможем в написании вашей работы!