Случайной величины

Закон распределения вероятностей дискретной

Виды случайных величин.

Вероятностей.

Определение: Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, заранее не известное и зависящее от случайных причин, которые заранее не могут быть учтены.

Пример: Число родившихся мальчиков среди 100 новорожденных есть случайная величина, которая имеет следующие возможные значения: 0, 1, 2, …, 100.

Будем обозначать случайные величины прописными буквами X, Y, Z и т.д., а их возможные значения – строчными: x, y, z.

Пример: Расстояние, которое пролетит снаряд при выстреле из орудия – случайная величина, т.к. зависит не только от установки прицела, но и от многих других факторов: ветра, температуры и т.п. Их невозможно полностью учесть.

Определение: Дискретной (прерывной) называют случайную величину, которая принимает отдельные, изолированные возможные значения с определёнными вероятностями.

Число возможных значений дискретной случайной величины может быть конечным или бесконечным.

Определение: Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка.

Число возможных значений непрерывной случайной величины бесконечно.

Заметим, что данное определение непрерывной случайной величиныне является точным. Более строгое определение будет дано позднее.

Определение: Законом распределениявероятностей дискретной случайной величины называют соответствие между её возможными значениями и их вероятностями.

Его можно задать таблично, аналитически (в виде формулы) и графически. В виде таблицы закон распределения имеет вид:

X			…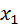
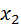
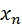
P			…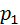

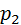
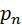
Так как в одном испытании случайная величина принимает одно и только одно возможное значение, то события 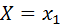, , 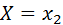…, 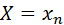образуют полную группу. Следовательно,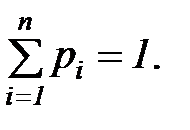

Если множество возможных значений X бесконечно (счётно), то ряд 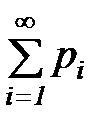сходится и его сумма равна 1:

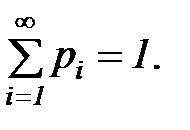
Пример: В денежной лотерее выпущено 100 билетов. Разыгрывается один выигрыш в 50 руб. и 10 выигрышей по 1 руб. Найти закон распределения случайной величины X – стоимости возможного выигрыша для владельца одного лотерейного билета.

Решение: Возможные значения X: 50, 1, 0.

Их вероятности: p₁ = 0,01; p₂ = 0,1; p₃ = 0,89.

Составим закон распределения вероятностей:

X	50	1	0
P	0,01	0,1	0,89

Контроль вычислений: 0,01 + 0,1 + 0,89 = 1.

Графически закон распределения вероятностей дискретной случайной величины можно представить в виде многоугольника распределения: в прямоугольной системе координат ставят точки (x_i, p_i) и соединяют их отрезками прямых.

Построим многоугольник распределения по данным предыдущего примера:

P   0,89

0,1

50 X

Пример: Написать закон распределения случайной величины X – числа появлений «орла» при бросании n монет.

Решение: Вероятность любого значения X вычисляется по одной и той же формуле:

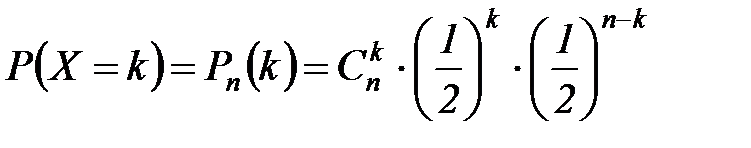
Тогда искомый закон распределения вероятностей имеет вид:

Х	0	1	…	n
Р

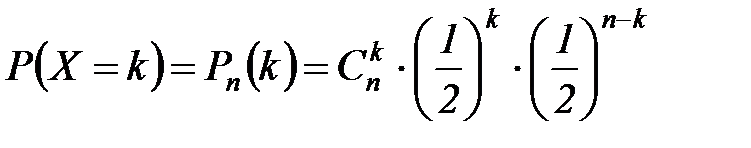– аналитическое выражение искомого закона.

Заметим, что закон распределения полностью характеризует случайную величину.

Дата добавления: 2014-12-27