Баланса. Модель Леонтьева

Экономико-математическая модель межотраслевого

Основные балансовые соотношения

Первое балансовое соотношение выражает связь между первым и вторым разделами балансовой модели

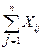+ y_i = X_i, i = 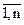, (3.3)

т.е. валовой выпуск отрасли равен сумме промежуточного и конечного продукта.

Второе балансовое соотношение выражает связь между первым и третьим разделами балансовой модели

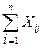+ Z _j = X_j, j = 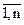, (3.4)

т.е. общие расходы отрасли равны сумме материальных затрат и добавленной стоимости.

Третье балансовое соотношение выражает связь между вторым и третьим разделами балансовой модели

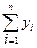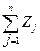= , (3.5)

т.е. сумма конечной продукции отраслей равна сумме добавленной стоимости этих отраслей.

Запишем первую систему балансовых соотношений, характеризующих распределение продукции отраслей материального производства:

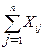+ y_i = X_i, i = .

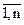Предположим, что межотраслевой поток продукции, идущей из i -ой отрасли в j -ю, прямо пропорционален валовому выпуску той отрасли, куда они направляются, т.е.

X_ij = а_ij × X_j. (3.6)

Коэффициенты пропорциональности а _ij называются коэффициентами прямых материальных затрат и характеризуют количество продукции i –й отрасли, необходимой для выпуска единицы продукции j –й отрасли. Будем полагать, что коэффициенты а _ij постоянны в некотором промежутке времени, охватывающем как отчетный, так и предстоящий (планируемый) период.

Подставим выражение (3.6) в первое балансовое соотношение

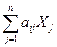+ y_i = X_i, i = 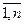. (3.7)

Выражение (3.7) называется системой уравнений межотраслевого баланса или экономико-математической моделью межотраслевого баланса, или моделью Леонтьева. Модель Леонтьева в матричном виде

АХ + Y = Х, (3.8)

где

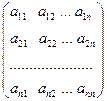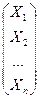А = , Х = , Y = .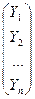

Можно сформулировать три типа задач межотраслевого баланса:

1. Известны коэффициенты прямых материальных затрат (а_ij; i, j = 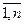) и объёмы конечного продукта всех отраслей y_i. Найти объёмы валового выпуска каждой отрасли X_i.

2. Известны объёмы валового выпуска всех отраслей X_i и коэффициенты прямых материальных затрат а_ij. Найти объёмы конечной продукции каждой отрасли y_i.

3. Известны коэффициенты прямых материальных затрат а_ij. Заданы объёмы валового выпуска для части отраслей и объёмы конечной продукции для всех остальных отраслей. Найти объёмы конечной продукции для первых отраслей и объёмы валового выпуска для вторых.

Дата добавления: 2014-12-27