Решение задачи. Стационарное распределение температуры в стержне описывается системой уравнений

Стационарное распределение температуры в стержне описывается системой уравнений

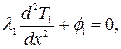
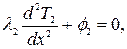
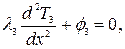(4.2)

где ф₁, ф₂, ф₃ - объемные плотности внутренних источников теплоты;

λ₁, λ₂, λ₃-теплопроводности материалов, Вт/м ⁰С;

Объемные плотности внутренних источников теплоты определяются по следующим выражениям:

ф₁ = I²ρ₁/A², ф₂ = I²ρ₂/A², ф₃ = I²ρ₃/A², (4.3.)

где ρ₁, ρ₂, ρ₃, - удельные сопротивления проводников, Ом∙мм²/м;

A - площадь поперечного сечения стержня, м²;

I - сила тока, А.

ф₁=1²∙0,1∙10^-4/(1,25∙10^-3) ²=6,34 Вт/м³;

ф₂=1²∙0,028∙10^-4/(1,25∙10^-3) ²=1.77 Вт/м³;

ф₃=1²∙0,15∙10^-4/(1,25∙10^-3) ²=9,5 Вт/м³;

Узлы 1, 4, 6, 9 лежат на границах составного стержня, узлы 2, 3, 5, 7, 8 лежат внутри стержня. Границы конечных объемов проходят посередине между уз­лами. Тепловые кондуктивные сопротивления равны R_i = h_i /λ₁S, i = 1,2,3, R_i = h_i /λ₂S, i = 4,5, R_i = h_i /λ₃S i = 6,7,8; конвективное тепловое со­противление R₉ = 1/αS, где α - задано. Независимые источники внутренних тепловых потоков Ф_i, i = 1,..., 9, включенные в тепловую схему равны

Ф_i=Aф₁∆_i-1 i = 1,2,3; Ф₄=Aф₁∆’₃+Aф₂∆’’₃; Ф₅=Aф₂∆₄;

Ф₆=Aф₂∆’₅+ Aф₃∆’’₅; Ф_i=Aф₃∆_i-1, i = 7,8,9. (4.4)

Подставляя данные в выражения (4.4) находим

Ф1= 1,25∙10^-3 ∙6,34∙0,02=1,59∙10^-4 Вт;

Ф2= 1,25∙10^-3 ∙6,34∙0,04=3.18∙10^-4 Вт;

Ф3=1,25∙10^-3 ∙6,34∙0,04=3,18∙10^-4 Вт;

Ф4=1,25∙10^-3 ∙6,34∙0,02+1,25∙10^-3 ∙1.77∙0,02=2,04∙10^-4 Вт;

Ф5= 1,25∙10^-3 ∙1.77∙0,04=8,9∙10^-5 Вт;

Ф6=1,25∙10^-3 ∙1.77∙0,02+1,25∙10^-3 ∙9.5∙0,02=2,83∙10^-4 Вт;

Ф7=1,25∙10^-3 ∙9.5∙0,04=4,77∙10^-4 Вт;

Ф8=1,25∙10^-3 ∙9.5∙0,04=4,77∙10^-4 Вт;

Ф9=1,25∙10^-3 ∙9.5∙0,02=2.39∙10^-4 Вт;

В соответствии с нумерацией узлов и ветвей и выбранными направлениями в ветвях (в данном случае номера ветвей совпадают с номерами тепловых со­противлений), матрица инциденций А имеет размерность 9×10 и равна

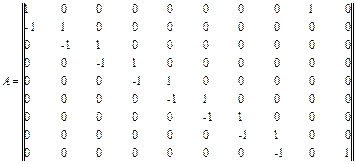(4.5)

Напомним, что согласно алгоритму, изложенному выше, в матрицу инциден­ций не входят ветви с независимыми источниками тепловых потоков. Матрица проводимостей G диагональная, ее диагональные элементы равны g_i = R^-_i¹, i = 1,2,..., 10.

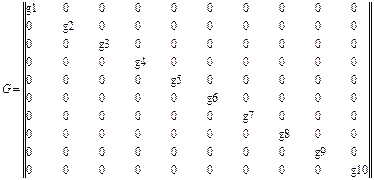(4.6)

Вектор-столбец независимых источников тепловых пото­ков Q равен

Q =||Ф1Ф2 Ф3 Ф4 Ф5 Ф6 Ф7 Ф8 Ф9||^Т. (4.7)

Вектор-столбец известных температур независимых источников температур равен

Т_а = ||0 0 0 0 0 0 0 0 Та1 Tа2 || ^T. (4.8)

Вектор-столбец неизвестных температур Т = || Т₁T₂… T₉ || ^T в узлах тепловой схемы определяется матричным уравнением

AGA^TT = Q + AGT_а (4.9)

Примем В=АGA^T и выразив Т, представим (3.8) в виде следующего выражения:

Т=В^-1∙Q+ В^-1∙A∙G∙T_a (4.10)

Подставив все известные величины в выражение (4.10) находим распределение температур в узлах стержневого элемента:

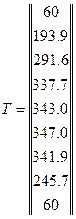(4.11)

Распределение температуры в составном стержневом термодинамическом элементе представлены на рис. 4.9

Дата добавления: 2014-12-27