Решение задачи. Двумерное растекание теплоты в области со сложной границей

Постановка задачи.

Двумерное растекание теплоты в области со сложной границей

Ра­ссмотрим одномерную область, имеющую прямоугольный вырез (рис. 3.1), и проведем анализ растекания потока теплоты в районе угла выреза.

Для решения задачи необходимо принять следующие начальные данные:

1) граничные условия 3 рода;

2) температуры: Та1=800 ⁰С; Та2=50 ⁰С; Та3=30 ⁰С;

3) коэффициент теплопроводности материала λ= 0,8 Вт/м ⁰С;

4) коэффициенты теплоотдачи α₁=70 Вт/м ^{2 0}С, α₂=100 Вт/м ^{2 0}С;

5) толщина материала δ=0,05 м;

а) б)

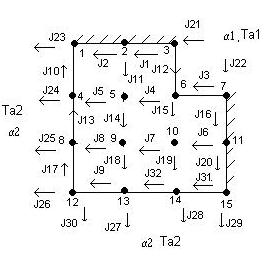
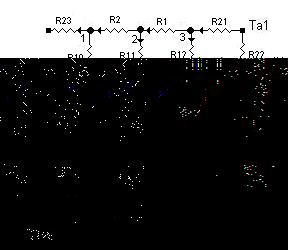
Рисунок 4.10 Одномерная область, имеющая прямоугольный вырез (а) и тепловая схема

Разобьем область на конечные объемы, в центре которых расположены узлы. Пронумеруем узлы от 1 до 15 как показано на рис. 3.1. Составим уравнения баланса потоков теплоты для каждого из узлов:

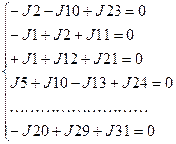(4.12)

Согласно уравнению (3.1) строим матрицу инциденции A, которая в данной задаче имеет размерность 15*32:

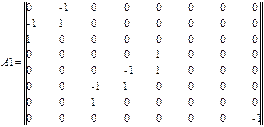
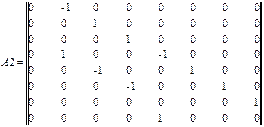
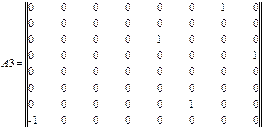
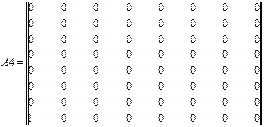
Для того, чтобы составить из двух или более матриц одну, в MathCAD предусмотрены две матричные функции:

augment – матрица, сформированная слиянием матриц-аргументов слева направо;

stack - матрица, сформированная слиянием матриц-аргументов сверху вниз.

Используя функцию augment, объединим матрицы A1, A2, A3 и A4 в одну, записав следующее:

A11=augment (A1, A2, A3, A4) (4.13)

Затем составим вторую часть матрицы A.

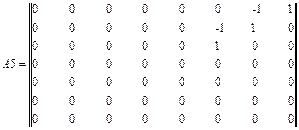
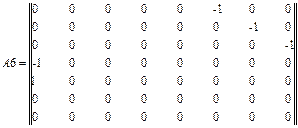
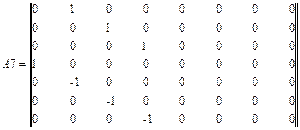
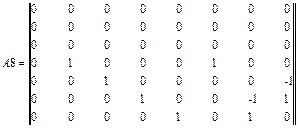
Объединим матрицы в одну:

A22= augment (A5, A6, A7, A8) (4.14)

Окончательная матрица A образуется в результате слияния матриц A11 и A22 при помощи функции stack:

A=stack (A11, A22) (4.15)

Построим матрицу проводимостей G размерностью 32*32:

, ,

, ,

.

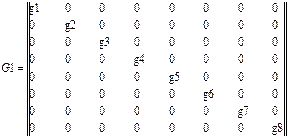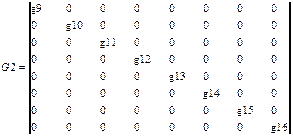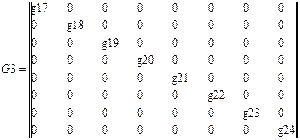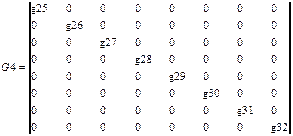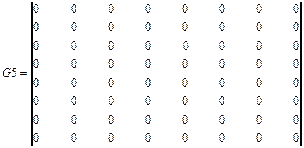Используя функцию augment, объединим матрицы в одну, записав следующее:

G11=augment (G1, G5, G5, G5)

G22=augment (G5, G2, G5, G5)

G33=augment (G5, G5, G3, G5) (4.16)

G44=augment (G5, G5, G5, G4)

Затем, чтобы получить окончательную матрицу G, необходимо воспользоваться функцией stack и объединить матрицы G11, G22, G33, G44:

G=stack (G11, G22, G33, G44) (4.17)

Вектор-столбец известных температур в ветвях тепловой схемы равен:

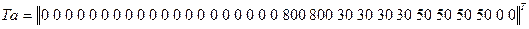(4.18)

Примем В=АGA^T и выразив Т, представим в виде следующего выражения:

Т= В^-1∙A∙G∙T_a (4.19)

Подставив все известные величины в выражение находим распределение температур в узлах:

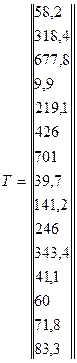
(4.20)
4.4.7 Двумерное растекание теплоты на границе 2-х материалов

Рассмотрим растекание потока теплоты вдоль прямой границы, разделяющей два материала. Разобьем область на конечные объемы. В области границы раздела двух материалов конечные объемы расположим так, чтобы их внутренние узлы, лежащие в их центре, принадлежали границе раздела. Область контакта двух материалов (а), ее разбиение на конечные объемы, расположение узлов и тепловая схема (б) представлены на рис. 4.11.

а) б)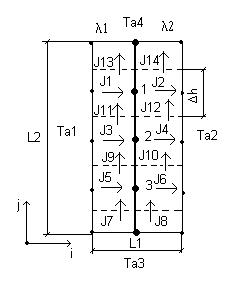

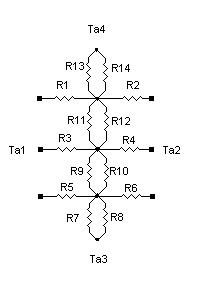
Рис 4.11

Дата добавления: 2014-12-27