
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Решение задачи. Зададим граничные условия 3 рода, т.е
Постановка задачи.
Зададим граничные условия 3 рода, т.е. на границах стержня происходит теплообмен со средой. Для решения задачи примем следующие начальные данные:
· материал стержня – сталь;
· температура среды и коэффициент теплоотдачи со стороны левой границы стержня равны: Та1=100 0С и α1=4000 Вт/м2 0С, со стороны правой – Та2=200С и α2=500 Вт/м2 0С;
· длина стержня L = 0,09 м;
· коэффициент теплопроводности материала стержня λ = 50 Вт/м 0С;
· площадь поперечного сечения A = 3,14∙10-4 м2;
· плотность стали ρ = 7800 кг/м3;
· теплоемкость с=460 Дж/кг0С;
· расстояние h между узлами равно 0,01 м.
Разобьем длину стержня сечениями перпендикулярными оси x на 10 конечных объемов длиной h=0.01м. Соответствующая тепловая схема приведена на рис.3.1. В центре каждого объема поместим по одному узлу, при этом номер узла совпадает с номером объема. Пронумеруем узлы тепловой схемы так, как показано на рис.3.1 от узла 1 (на левом торце стержня) до узла 10 (на правом торце стержня).
а)

б)
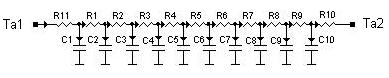
Рисунок 4.12. Стержень, теплоизолированный с боковой поверхности (а) и его тепловая схема (б)
Составим матрицу инциденции A, которая в рассматриваемом примере имеет размерность 10*11:
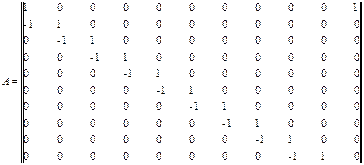 (4.25)
(4.25)
Матрица проводимостей G имеет размерность 11*11, является диагональной:
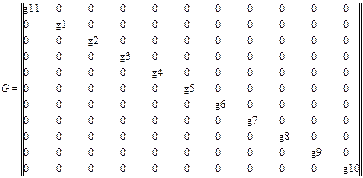 (4.26)
(4.26)
Матрица теплоемкостей C имеет размерность 10*10, является диагональной и ее диагональные элементы равны:
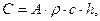 , (4.27)
, (4.27)
где A – площадь сечения стержня, м2;
ρ – плотность стали, кг/м3;
с – теплоемкость стали;
h – расстояние между границами объема, м.
Строим матрицу C:
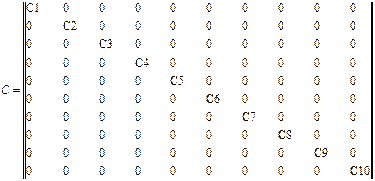 (4.28)
(4.28)
Вектор-столбец Ta известных температур среды равен:
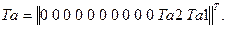 (4.29)
(4.29)
Матрично-топологическое уравнение тепловой схемы относительно вектора неизвестных температур в узлах схемы 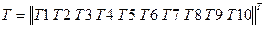 имеет вид:
имеет вид:
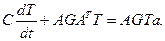 (4.30)
(4.30)
Уравнение (4.30) является матричным дифференциальным уравнением в обыкновенных производных и описывает нестационарные температуры в узлах тепловой схемы.
Примем начальные температуры в узлах равными 0 0С, т.е. 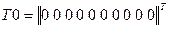
Рассмотрим решение нестационарного матричного уравнения
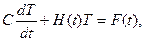 (4.31)
(4.31)
где H(t) – положительно определенная матрица для всех t ≥ 0 и равна 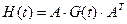 ;
;
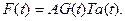
с начальным условием
T(0)=T0, (4.32)
Для решения нестационарного матричного уравнения (3.7) с начальным условием (4.32) используем явный метод Эйлера. явный метод Эйлера приводит к итерационной процедуре:
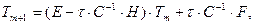 (4.33)
(4.33)
где m – номер итерации;
τ – шаг по времени;
E – диагональная единичная матрица;
Диагональная единичная матрица E, имеющая размерность 10*10 равна
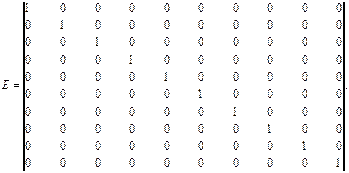 (4.34)
(4.34)
В явном методе Эйлера значение вектора-столбца температуры Tm в следующий момент времени tm находится пересчетом по формуле (3.9) на основании известного значения температуры Tm-1 в предыдущий момент времени tm-1.
Зададим дополнительные условия для решения задачи:
4) шаг по времени τ = 2;
5) максимальное время M = 100 с.;
6) условие m…M;
Подставив все известные величины в уравнение (4.34), найдем температуры в узлах через 1с., 40с., и 100 с.:
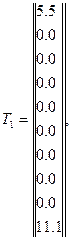
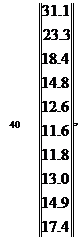
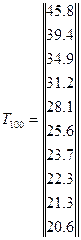 .
.
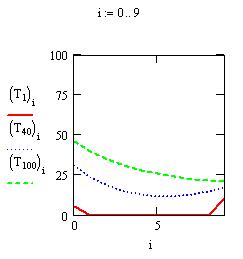
Рисунок 4.13. График зависимости температуры от безразмерной координаты в моменты времени через 1, 40 и 100 с.
|
|
Дата добавления: 2014-12-27; Просмотров: 534; Нарушение авторских прав?; Мы поможем в написании вашей работы!