Решение задачи. Однородный стержневой элемент, теплоизолированный с боковой поверхности

Однородный стержневой элемент, теплоизолированный с боковой поверхности

Рассмотрим одномерный стержень, поперечное сечение которого столь мало, чтобы можно было пренебречь изменением температуры по его сечению. В этом случае, температурное поле стержня является одномерным и изменяется только по оси х, направленной по длине стержня.

Постановка задачи.

Зададим граничные условия 3 рода, т.е. на границах стержня происходит теплообмен со средой. Для решения задачи примем следующие начальные данные:

· температура среды и коэффициент теплоотдачи со стороны левой границы стержня равны: Та1=300 ⁰С и α1=5 Вт/м^{2 0}С, со стороны правой – Та2=0⁰С и α2=20 Вт/м^{2 0}С;

· длина стержня L равна 20 мм;

· коэффициент теплопроводности материала стержня λ = 0,1 Вт/м ⁰С;

· радиус сечения стержневого элемента r= 5 мм.

Разобьем длину стержня сечениями перпендикулярными оси x на три конечных объема длиной Δx=0.01мм и площадью сечения A, равной площади поперечного сечения стержня. Соответствующая тепловая схема приведена на рис.3.1. В центре каждого объема поместим по одному узлу, при этом номер узла совпадает с номером объема. Пронумеруем узлы тепловой схемы так, как показано на рис.3.1 от узла 1 (на левом торце стержня) до узла 3 (на правом торце стержня).

а)

б)

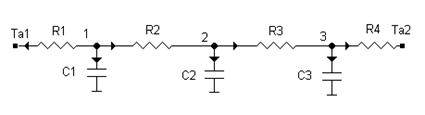
Рисунок 4.14 Одномерный стержень, разбитый на конечные объемы (а) и его тепловая схема (б)

Рассмотрим баланс потока теплоты в i-ом выделенном объеме, воспользовав­шись интегральным уравнением теплового баланса

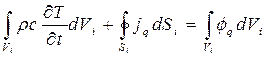(4.35)

где Vi = A ∆ xi – объем i-го элемента;

S_i- площадь всей поверхности выде­ленного i -го объема. Индекс i относит рассматриваемые переменные к i-му выделенному объему.

Поверхностный интеграл в левой части уравнения (3.1) выражает суммар­ный тепловой поток, пересекающий поверхность выделенного i-ro объема. Учи­тывая, что тепловой поток вдоль стержня одномерен (не изменяется в направле­нии перпендикулярном оси х), а тепловой поток с боковой поверхности стержня отсутствует (поскольку рассматривается теплоизолированный с боковой по­верхности стержень) можно записать, например, для узла 2, что

(4.36)

где Q₂ и Q₃ - тепловые потоки на левой и павой границах выделенного объема.

За положительное направление вектора теплового потока принято направление, соответствующее вытеканию из объема теплового по­тока.

Так как, рассматриваемая задача является стационарной, т.е. dT/dt =0 и внутренние источники теплоты 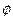отсутствуют, то уравнение (3.1) принимает следующий вид:

(4.37)

Уравнения теплового баланса, записанные для узлов тепловой схемы, имеют вид:

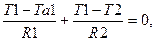
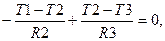(4.38)

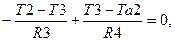
где R1, R2, R3, R4 – тепловые сопротивления выделенных объемов между узлами.

Баланс потоков теплоты, протекающих в ветвях соединенных с узлами 1, 2, 3 выражаются следующими уравнениями

(4.39)

Ориентированный граф тепловой схемы представлен на рис.3.2. Номера ветвей указаны в кружках.

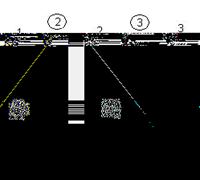
Рисунок 4.15 Ориентированный граф тепловой схемы

В стационарном случае, вектор-столбец температур Т описывается матричным уравнением, при , т.е.

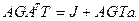(4.40)

Введя вектор-столбец тепловых потоков ветвей Q=||Q1 Q2 Q3 Q4||^Т, систему уравнений можно записать в матричном виде

AQ=0 (4.41)

Матрица A называется матрицей инциденции, для рассматриваемого случая имеет размерность 3*4 и равна:

(4.42)

Уравнение является, по существу, дискретным уравнением баланса тепловых потоков в тепловой схеме. Вид матрицы A нетрудно понять. Строки матрицы соответствуют узлам графа и расположены согласно их номерам от 1 до 3 сверху вниз, а столбцы матрицы соответствуют ветвям графа, причем номер столбца равен номеру ветви в тепловой схеме.

Разности температур в ветвях графа можно представить в виде вектора- столбца ΔT:

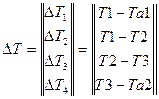(4.43)

Введя вектор столбец температур узлов графа

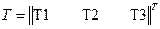(4.44)

простым перемножением легко убедится, что вектор-столбец (4.44) можно записать в следующем матричном виде:

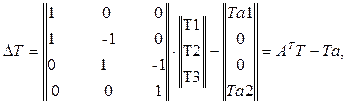(4.45)

(4.46)

где 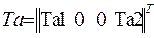- вектор-столбец известных температур в ветвях 1 и 4 тепловой схемы.

Сравнение матрицы инциденций A (3) и матрицы в соотношении (6) показывает, что последняя матрица является транспонированной по отношению к матрице А, т.е. равна А^Т, поэтому вектор-столбец ΔТ (4) в соотношении (6) можно записать в матричном виде через транспонированную матрицу инциденций А^Т, т.е.

ΔТ=А^ТТ (4.47)

Полученные матрично-топологические соотношения устанавливают связь между тепловыми потоками в ветвях тепловой схемы и преобразование узловых температур в разности температур в ветвях. Матрица инциденций А отображает структуру тепловой схемы.

Матрица А, естественным образом, была получена из системы уравнений баланса тепловых потоков в узлах графа.

Для исчерпывающего описания графа тепловой схемы необходимо располагать соотношениями, связывающими тепловые потоки и разности температур в ветвях графа, в соответствии с элементами схемы, представленными ветвями.

Выше было показано, что тепловой поток Q_i в i-ой ветви равен Q_i=g_iΔT_i.

Тогда связь векторов-столбцов Q и ΔТ может быть записана в следующем матричном виде:

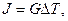(4.48)

где G – квадратная матрица проводимостей ветвей размерностью М*М, М – количество ветвей графа.

Матрица проводимостей G формируется следующим образом: если ветвь i представляет собой тепловую проводимость g_i (кондуктивную или конвективную), то элемент ii матрицы G равен g_i.

Конвективные тепловые проводимости с торцов стержня, которые входят в ветви с номерами 1 и 4 равны соответственно 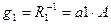и .

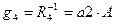Тепловые кондуктивные проводимости, которые входят в ветви с номерами 2 и 3 равны 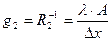и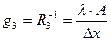

Строим матрицу проводимостей G:

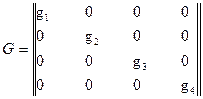(4.49)

Введем матрицу B, которая находится по формуле:

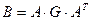(4.50)

где А^Т – транспонированная матрица А.

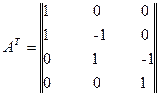(4.51)

Подставляя выражения (3.8), (3.12), (3.15) и (3.16) в уравнение (3.18)

(4.52)

находим искомые температуры в узлах стержневого элемента.

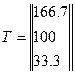(4.53)

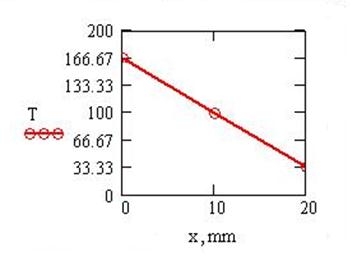
Т1=166.7 ⁰С;

Т2=100 ⁰С;

Т3=33.3 ⁰С.

Распределение температуры в стержневом термодинамическом элементе представлены на рис. 4.16

Рисунок 4.16 График распределения температур по длине одномерного стержня

Дата добавления: 2014-12-27