
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тема 5. Исследование функции и построение графика
|
|
|
|
Определение Внутренняя точка 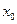 интервала
интервала 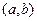 называется точкой максимума (минимума)функции
называется точкой максимума (минимума)функции  , если существует такое
, если существует такое  , что для всех
, что для всех 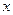 из интервала
из интервала  , содержащегося внутри интервала
, содержащегося внутри интервала 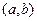 , выполняется неравенство
, выполняется неравенство  (
( ). Точки максимума и минимума называют точками экстремума (локального экстремума) функции. Точки, в которых производная обращается в ноль, называют стационарными точками.
). Точки максимума и минимума называют точками экстремума (локального экстремума) функции. Точки, в которых производная обращается в ноль, называют стационарными точками. 
Приведем формулировки теорем, используемых при исследовании функций.
Достаточное условие строгого возрастания (убывания) функции:
Если  (
(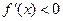 ) в интервале
) в интервале 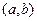 , то
, то  строго возрастает (убывает) в этом интервале. Промежутки, в которых функция возрастает (убывает), называются промежутками монотонности функции. Чтобы найти промежутки монотонности функции необходимо:
строго возрастает (убывает) в этом интервале. Промежутки, в которых функция возрастает (убывает), называются промежутками монотонности функции. Чтобы найти промежутки монотонности функции необходимо:
- Найти область определения функции;
- Найти производную функции;
- Приравнять производную к нулю и определить ее корни (стационарные точки), а также найти точки, в которых производная не существует, а функция определена;
- Определить знак производной в каждом из промежутков, на которые разбивается полученными точками область определения функции.
Необходимое условие экстремума функции:
Если функция  дифференцируема в точке
дифференцируема в точке 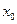 и достигает в этой точке максимума (минимума), то
и достигает в этой точке максимума (минимума), то  .
.
Точками экстремума могут быть только те точки, в которых производная равна нулю, либо не существует. Точки, в которых производная равна нулю или не существует, называют точками, подозрительными на экстремум, или критическими точками.
Достаточные условия экстремума функции:
Если при переходе через точку 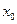 , подозрительную на экстремум, производная меняет знак, то точка
, подозрительную на экстремум, производная меняет знак, то точка 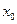 является точкой экстремума. При этом если в некоторой окрестности точки
является точкой экстремума. При этом если в некоторой окрестности точки 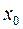
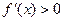 для
для 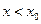 и
и 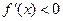 для
для  , то
, то 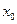 является точкой максимума. Если же в этой окрестности
является точкой максимума. Если же в этой окрестности 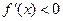 для
для 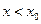 и
и 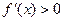 для
для  , то
, то 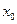 – точка минимума.
– точка минимума.
Другим достаточным признаком существования экстремума в стационарной точке 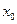 является условие
является условие  (тогда это точка максимума) и
(тогда это точка максимума) и 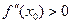 (тогда это точка минимума). При этом считается, что
(тогда это точка минимума). При этом считается, что  имеет непрерывную вторую производную в некоторой окрестности точки
имеет непрерывную вторую производную в некоторой окрестности точки 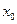 .
.
Определение График функции  называетсявыпуклым в интервале
называетсявыпуклым в интервале  , если он расположен ниже касательной проведенной в любой точке этого интервала.
, если он расположен ниже касательной проведенной в любой точке этого интервала.
Определение График функции  называется вогнутымв интервале
называется вогнутымв интервале 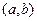 , если он расположен выше касательной, проведенной в любой точке этого интервала.
, если он расположен выше касательной, проведенной в любой точке этого интервала.
Достаточные условия выпуклости (вогнутости) графика функции:
Если 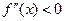 в интервале
в интервале 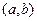 , то график функции является выпуклым в этом интервале; если же
, то график функции является выпуклым в этом интервале; если же  , то в интервале
, то в интервале 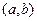 график функции вогнутый.
график функции вогнутый.
Точка 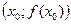 графика функции, отделяющая его выпуклую часть от вогнутой, называется точкой перегиба. Если
графика функции, отделяющая его выпуклую часть от вогнутой, называется точкой перегиба. Если 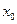 ─ абсцисса точки перегиба графика функции
─ абсцисса точки перегиба графика функции  , то вторая производная равна нулю или не существует в этой точке. Точки, в которых
, то вторая производная равна нулю или не существует в этой точке. Точки, в которых 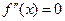 или
или  не существует, называются критическими точками второго рода.
не существует, называются критическими точками второго рода.
Если при переходе через критическую точку второго рода 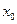 вторая производная меняет знак, то точка
вторая производная меняет знак, то точка 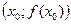 есть точка перегиба.
есть точка перегиба.
Определение Прямая l называется асимптотой кривой y = f(x), если расстояние точки М(х,у) на кривой от прямой l стремится к нулю при неограниченном удалении этой точки по кривой от начала координат, (т.е. при стремлении хотя бы одной из координат точки к бесконечности).
Прямая  является вертикальной асимптотой кривой y = f(x), если:
является вертикальной асимптотой кривой y = f(x), если:
 или
или 
Прямая  является горизонтальной асимптотой кривой y = f (x), если существует
является горизонтальной асимптотой кривой y = f (x), если существует  или
или 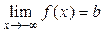
Прямая  является наклонной асимптотой кривой y = f(x), если существуют пределы:
является наклонной асимптотой кривой y = f(x), если существуют пределы:
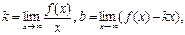
или 
При исследовании функции и построении ее графика удобно придерживаться следующего плана:
- Найти область определения функции.
- Определить четность (нечетность), периодичность функции.
- Найти точки разрыва.
- Определить точки пересечения графика с осями координат.
- Найти точки экстремума и вычислить значения функции в этих точках.
- Определить интервалы возрастания и убывания функции.
- Найти точки перегиба, интервалы выпуклости и вогнутости.
- Определить асимптоты.
- Найти предельные значения функции при аргументе, стремящемся к границам области определения.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 470; Нарушение авторских прав?; Мы поможем в написании вашей работы!