
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Средняя арифметическая простая
|
|
|
|
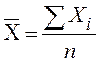 ,
,
где åХi – сумма вариантов признака,
n – число единиц, обладающих данным признаком.
Нужно помнить, что средняя арифметическая взвешенная применяется в тех случаях, когда известна величина признака Хi и частота его проявления у каждой единицы совокупности fi (в зависимости от условия частота может быть заменена на частность). Например, рассчитаем средний уровень заработной платы по данным о заработной плате по каждому отделу и численности работников каждого отдела. Используем формулу средней арифметической взвешенной
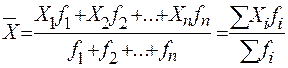 ’
’
где 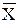 – средняя заработная плата на предприятии;
– средняя заработная плата на предприятии;
Х i – уровень заработной платы по каждому отделу;
f i – численность работников в каждом отделе;
X i f i – фонд заработной платы по каждому отделу.
Средняя гармоническая взвешенная применяется в тех случаях, когда известна величина признака (Хi) и величина объема варьирующегося признака (Xifi) для каждой единицы совокупности, а значения частот (fi) неизвестны.
Например, если в условии задачи даны показатели уровня заработной платы и фонда заработной платы по каждому отделу, то средний уровень заработной платы будет исчисляться по формуле средней гармонической взвешенной
å W i
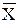 = ————,
= ————,
å W i / X i
где Х i – уровень заработной платы каждого работника;
W i – фонд заработной платы по каждому работнику (Х i • f i = W i).
Аналогичен подход к расчету других средних показателей: цены, затрат времени, процента выполнения плана, товарооборота и т.д.
Необходимо дать анализ полученным средним и итоговым показателям и сформулировать вывод.
Структурные средние величины.
Мода (Мо) – величина признака, которая встречается в изучаемом ряду чаще всего.
Медиана (Ме) – величина признака, находящаяся в середине вариационного ряда. Медиана делит ряд пополам, по обе стороны от нее (вверх и вниз) находится одинаковое количество единиц совокупности.
Для интервальных рядов распределения мода определяется по формуле
f мо – fм0 -1
Мо = Хмо + h мо ————————————,
(fмо – fмо-1) + (fмо – fмо+1)
где Хмо – начальное значение интервала, содержащего моду;
h мо – величина модального интервала;
fмо – частота модального интервала;
fмо-1 – частота интервала, предшествующего модальному;
fмо+1 – частота интервала, следующего за модальным.
Медиана в интервальном ряду находится следующим образом:
0,5 • åf – åfме -1
Ме = Х ме + h ме ———————
fме
Х ме – начальное значение интервала, содержащего медиану;
h ме – величина медианного интервала;
åf – сумма частот ряда (численность ряда);
S fме-1 – сумма накопленных частот, предшествующих медианному интервалу;
fме – частота медианного интервала.
Кроме Mo и Me ввариантных рядах могут быть определены и другие структурные характеристики – квантили. Квантили предназначены для более глубокого изучения структуры ряда распределения. Квантиль – это значение признака, занимающее определенное место в упорядоченной по данному признаку совокупности. Различают следующие виды квантилей:
• квартили (Q1/4,Q2/4 =Me,Q3/4 — значения признака, делящие
упорядоченную совокупность на 4 равные части;
• децили (d1,d2....d9 — значения признака, делящие
совокупность на 10 равных частей;
• перцентели – значения признака, делящие совокупность на
100 равных частей.
Если данные сгруппированы, то значение квартиля определяется по накопленным частотам: номер группы, которая содержит i -й квантиль. Определяется как номер первой группы от начала ряда, в котором сумма накопленных частот равна или превышает i ·N, где i – индекс квантиля.
Система показателей, с помощью которой вариация измеряется, характеризуют ее свойства.
Наиболее простым является расчет показателя размаха вариации R как разницы между максимальным и минимальным значениями признака:
R = X max – Xmin.
Более строгими характеристиками являются показатели относительно среднего уровня признака. При вычислении показателей вариации необходимо учесть, что если средние показатели были вычислены по формулам арифметической или гармонической взвешенных, то и отклонения от средней также должны вычисляться по формулам взвешенного линейного отклонения, взвешенного квадрата отклонений, взвешенного среднего квадратического отклонения. Простейший показатель такого типа – среднее линейное отклонение как среднее арифметическое значение абсолютных значений отклонений п р изнака от его среднего уровня:
å | X i – 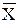 | |
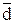 = —————;
n = —————;
n
| å | X i – 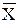 | f | f
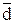 = —————.
åf = —————.
åf
|
Показатель среднего линейного отклонения широко применяется на практике. С его помощью анализируются ритмичность производства, состав работающих, равномерность поставок материалов. Однако в статистике наиболее часто для измерения вариации используют показатель дисперсии – средней арифметической квадратов отклонений каждого значения признака от средней арифметической.
å(Хi – 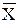 )2
s2 = ¾¾¾¾,
n )2
s2 = ¾¾¾¾,
n
| å(Хi – 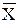 )2 f
s2 = ¾¾¾¾–.
åf )2 f
s2 = ¾¾¾¾–.
åf
|
Дисперсию можно определить и как разность между средним квадратом вариантов признака и квадратом их средней величины:
s2 = 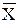 2 – ( 2 – (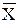 )2 , )2 ,
| åX2f
s2 = ——— – (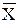 )2 .
åf )2 .
åf
|
Показатель s, равный Ös2, называется средним квадратическим отклонением. Рассмотренные показатели не всегда пригодны для сравнительного анализа вариации нескольких совокупностей в силу различия абсолютных величин. Для характеристики степени однородности совокупности, типичности, устойчивости средней, а также для других статистических оценок применяется коэффициент вариации, являющийся относительной величиной, выраженной в процентах.
s
n = –– • 100%.
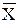
Как относительная величина коэффициент вариации абстрагирует различия абсолютных величин и дает возможность сравнивать степень вариации разных признаков, разных совокупностей. Чем больше коэффициент вариации, тем менее однородна совокупность и тем менее типична средняя, тем менее она характеризует изучаемое явление.
Решение задачи 3 должно способствовать закреплению навыков расчета показателей, характеризующих сущность выборочного наблюдения и определения ошибок выборки, а также расчета необходимой численности выборки.
Показатель представительности выборки следует рассчитывать как отношение выборочной характеристики к соответствующей характеристике генеральной совокупности, например для средней. Если показатели выборки незначительно отличаются от показателей генеральной совокупности (обычно в пределах ± 5%), значит, выборка отражает распределение генеральной совокупности. Рассчитанные по выборке значение параметра и его предельная ошибка позволят установить пределы, в которых будет заключено значение параметра в генеральной совокупности, при этом выводы гарантируются с определенной вероятностью. Например, генеральная совокупность будет иметь границы
 – t mx £
– t mx £  £
£  + t mx.
+ t mx.
При случайном простом отборе предельная ошибка выборочной средней

Предельная ошибка для выборочной доли
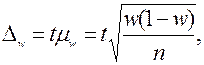
Предельная ошибка случайной бесповторной выборки определяется по аналогичным формулам с появлением сомножителя, который уменьшает величину ошибок:
а) предельная ошибка для средней:

б) предельная ошибка для доли:
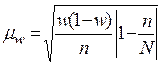 .
.
Чаще всего доверительную вероятность устанавливают равной 0,954 или 0,997 (величины коэффициентов доверия t равны соответственно 2 и 3).
Вероятность, которая принимается при расчете ошибки выборочной характеристики, называют доверительной. Чаще всего принимают доверительную вероятность равной 0,95; 0,954; 0,997 или даже 0,999. Доверительный уровень вероятности 0,954 означает, что только в 6 случаях из 1000 ошибка может выйти за установленные границы.
Задача 4 составлена на вычисление и усвоение аналитических показателей анализа динамических рядов.
Для выражения изменений уровней ряда динамики в абсолютных величинах вычисляется показатель абсолютного прироста DY. Он показывает, на сколько единиц увеличился (или уменьшился) уровень по сравнению с базисным, то есть за определенный период времени. Абсолютный прирост определяется как разность между уровнем изучаемого периода Yi и уровнем, принимаемым за базу сравнения:
DY = Yi – Yб .
Абсолютные приросты могут быть цепными и базисными. При определении цепных абсолютных приростов DYu за базу сравнения принимается уровень предыдущего периода Yi–1, и расчет абсолютных приростов производится по формуле
DYц = Yi –Yi – 1.
При определении базисных абсолютных приростов DYб за базу сравнения принимается постоянный уровень.
D Yб = Yi –Yб .
Для суждения о среднем изменении абсолютных DYц приростов вычисляется средний абсолютный прирост  . Он может быть вычислен по цепным абсолютным приростам, базисным абсолютным приростам или уровнем ряда:
. Он может быть вычислен по цепным абсолютным приростам, базисным абсолютным приростам или уровнем ряда:
SDY ц
D  = ———, m = n – 1,
= ———, m = n – 1,
m
где m – число интервалов в ряду динамики;
DY бn Yn – Yб
D  = ——, или D
= ——, или D  = ———,
= ———,
m m
Относительными показателями динамики являются коэффициенты роста К и коэффициенты прироста DК.
Коэффициент роста показывает, во сколько раз увеличился уровень по сравнению с базисным или предыдущим уровнем. Он определяется как отношение уровня изучаемого периода к уровню, принятому за базу сравнения:
Yi
К = –––.
Yб
Темп роста вычисляется в процентах и представляет собой произведение коэффициента роста на 100%, все преобразования коэффициентов роста сохраняются и для темпов роста.
При вычислении цепных коэффициентов роста за базу сравнения принимается уровень предыдущего периода:
Yi
К ц = –––––.
Yi– 1
При вычислении базисных коэффициентов роста за базу сравнения принимают постоянный уровень (как правило, уровень самого раннего периода).
Yi
К б = –––.
Yб
Между цепными и базисными коэффициентами роста существует определенная взаимосвязь: произведение последовательных цепных коэффициентов роста равно базисному коэффициенту роста за весь соответствующий период:
ПК ц = Кб,где П – знак произведения.
Соблюдается связь (через коэффициенты).
Для определения среднегодового коэффициента роста используется формула средней геометрической:

где ПКц – произведение цепных темпов роста в коэффициентах;
m – число цепных темпов роста (n – 1).
Если при определении темпов прироста DК предварительно были исчислены темпы роста Тр, то темпы прироста можно рассчитать по формуле:
DК = К – 1 или DТпр % = Тр% – 100%.
Для средних темпов роста и прироста сохраняет силу та же взаимосвязь, имеющая место между обычными темпами роста и прироста:
D 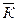 =
= 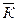 – 1 и D
– 1 и D 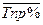 =
=  – 100%.
– 100%.
Показатель абсолютного значения одного процента прироста А% определяется как отношение в каждом периоде абсолютного прироста DY ц к темпу прироста DКц . Расчет этого показателя имеет экономический смысл только на цепной основе:
А% = DY ц / DК ц %.
При разных уровнях явления абсолютное значение 1% является разной величиной.
Аналитическое выравнивание ряда состоит в отыскании аналитической формулы кривой, которая наиболее точно отражала бы основную тенденцию изменения уровней в течение периода. Уравнение, выражающее уровни ряда динамики в виде некоторой функции времени, называют трендом.
Аналитическое выравнивание ряда динамики позволяет выявить более четким направление основной тенденции.
Рассмотрим технику выравнивания ряда по уравнению прямой. Параметры а0 и а1 искомой прямой определяются по методу наименьших квадратов. Составляется система нормальных уравнений:
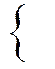
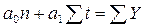


где t – порядковый номер интервала или момента времени.
Расчет параметров а0 и а1 упрощается, если за начало отсчета
t = 0 принять центральный интервал или момент. Тогда åt = 0, и система уравнений примет следующий вид:
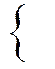
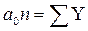


| åY | åYt | |
| Отсюда | а0 = ——–; | а1 = ——. |
| n | åt2 |
Аналитическое выравнивание ряда динамики позволяет выявить более четким направление основной тенденции.
Для расчета параметров уравнения и проверки надежности уравнения необходимо построить вспомогательную таблицу:
|
|
|
|
|
Дата добавления: 2014-12-23; Просмотров: 594; Нарушение авторских прав?; Мы поможем в написании вашей работы!