Модели развития операций по схеме простых процентов

МОДЕЛИ ФИНАНСОВО-КОММЕРЧЕСКИХ ОПЕРАЦИЙ

Педагогика: материалы к коллоквиумам

Инесса Олеговна Карелина

кандидат педагогических наук, доцент

Учебно-методическое пособие

Редактор И. О. Карелина

Филиал ФГБОУ ВПО «Ярославский государственный

педагогический университет им. К. Д. Ушинского» в г. Рыбинске

(филиал ЯГПУ в г. Рыбинске)

г. Рыбинск, ул. Свободы, 21

В любых коммерческих операциях финансовые расчеты прак­тически всегда привязываются к конкретным моментам време­ни (датам). Причем фактор времени играет не меньшую роль, чем размеры денежных сумм, и поэтому в коммерческих контрактах обязательно фиксируются сроки, даты, периодичность поступле­ния товаров, денежных средств или их выплат. Необходимость учета этого фактора определяется сущностью самого процесса коммерческой деятельности, финансирования и кредитования и связана с постулатом неравноценности денег в разные моменты времени. Этот постулат верен даже при отсутствии инфляции, поскольку в любой момент есть организации или частные лица (заемщики), нуждающиеся в кредитах на тот или иной период и готовые платить за такой заем (ссуду) определенную сумму, на­зываемую процентами.

Постулат неравноценности денег, связанный со временем, ставит под сомнение правомерность бухгалтерских операций суммирования денежных величин, относящихся к разным мо­ментам времени поступления денежных средств особенно при анализе управления коммерческой деятельностью на длитель­ные периоды.

Фактор времени в финансовой сфере учитывается с помощью процентной ставки как отношение суммы процентных денег, выплачиваемой за фиксированный отрезок времени, к величи­не ссуды. Интервал, к которому приурочена процентная став­ка, называют периодом начисления. Сумму процентных плате­жей определяют исходя из размера ссуды, общего ее срока и уровня процентной ставки. Начисление процентов чаще всего производится дискретно, а в некоторых случаях и в виде непре­рывных процентов.

В условиях рыночной экономики существуют различные ва­рианты инвестирования. В простейшем случае кредитор и заем­щик договариваются о величине кредита Р (первоначальная денеж­ная сумма), размере годовой процентной ставки (i %), сроке кре­дита и длительности периода начисления процентов. Математи­чески такая операция может быть представлена в виде сетевой модели простых процентов. По этой модели происходит накопле­ние общей суммы долга S за счет периодического, например еже­годного, начисления процентных денег (I _г). В соответствии с этим в конце первого года наращенная сумма будет равна:

S _г = Р + I _г;

к концу второго года -

S₂ = S г + I _г =Р + 2· I _г;

к концу третьего года -

S ₃ = S ₂ + I _г = P + 3· I _г;

к концу n -го года -

S_n = P + n · I _г.

В этом случае накопление суммы происходит по схеме про­стых процентов и образует возрастающую числовую последова­тельность:

S ₀, S ₁, S ₂, S ₃, …, S_n,

которая представляет собой арифметическую прогрессию с первым членом а₀= S ₀ и разностью прогрессии:

d = S ₂ - S ₁ = I _г.

Таким образом, математической моделью, отображающей изменение капитала по схеме простых процентов, является ариф­метическая прогрессия, в соответствии с которой любой ее член находится по формуле

S _n = a ₀ + d · n.

Процентная суммаопределяется по формуле

I = P· = P·i,

где i — относительная величина годовой ставки ссудного процента:

i = .

На этом основании модель накопления капитала по схеме простых процентов принимает вид

S = P + n·P·i = P· (l + n·i).

Следует заметить, что параметр п может быть как целым, так и дробным положительным числом

n = ,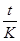

где t - продолжительность периода начисления процентов в днях;

К - количество дней в году (360, 365, 366).

Тогда приведенную модель можно записать в другом виде:

S = P .

В зависимости от содержания поставленной задачи, пользуясь этой моделью, можно определять различные показатели операции:

величину первоначальной (математическое дисконтирова­ние) суммы -

P = = ;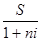

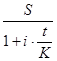относительную величину процентной ставки –

i = = · ;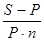

продолжительность года -

K = ;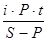

количество интервалов начисления (лет) -

n = ;

период начисления процентов (дней) -

t = K· ;

коэффициент наращения по простой процентной ставке -

k_н = = (1 + i·n).

Если на последовательных интервалах начисления про­центов п ₁ п ₂ п ₃ ..., п_т, устанавливаются разные ставки про­центов i ₁, i _2, i ₃,..., i_m, то сумма процентных денег составит

в конце первого интервала: I ₁= Р n ₁ i _l;

в конце второго интервала: 1 ₂= Р п ₂ i ₂;

в конце m -го интервала: 1_т = Р п_т i_m.

На этом основании можно записать, что за весь срок догово­ра наращенная сумма будет равна:

S = P + I ₁ + I ₂ + I ₃ +... + I_m =

= P + P·n ₁ ·i _l + P·n ₂ ·i ₂ + P·n ₃ ·i ₃ +... + P·n_m·i_m

S = P (l + ) = P·k_н.

Следовательно, коэффициент наращения равен:

k_н = 1 + .

Следует заметить, что в этом случае проценты начисляются всегда от величины первоначальной суммы Р.

В банковской практике различных стран срок в днях и рас­четное количество дней в году при начислении процентов опре­деляются по-разному. При германской практике подсчет числа дней основывается на длительности года в 360 дней и месяцев в 30 дней. При французской практике длительность года прини­мается равной 360 дням, а количество дней в месяце берется рав­ным фактической календарной длительности 28, 29, 30 или 31 день соответственно. При английской практике длительность года - 365 дней и длительность месяцев соответствует фактичес­кой длительности по календарю. Для удобства выполнения рас­четов пользуются сквозной нумерацией всех дней в году, пред­ставленной в табл. 7.1.1.

Пример 1. Определите количество дней для начисления про­центов при различной практике начисления, если вклад до вос­требования был размещен с 12.01 по 15.03.

Решение. 1. При германской практике количество дней для начисления процентов будет равно:

20(количество дней хранения вклада в январе) + 30(вфев­рале) + 15(вмарте) - 1(день приема и выдачи вклада считаются за один день) = 64дня.

2. При французской и английской практиках количество дней для начисления процентов составит:

20 + 28 + 15 -1=62дня (меньше, чем при германской прак­тике).

Пример 2. Вклад 300 тыс. руб. был положен в банк 20.05 при ставке 60% годовых. С 1 сентября банк снизил ставку по вкла­дам до 30% годовых. 25 октября вклад был закрыт.

Определите сумму начисленных процентов при английской, германской и французской практиках начисления.

Решение 1. При германской практике количество дней для начисления процентов по ставке 60% годовых равно: t _г1= 12 + 30 + 30 + 30 + 1 - 1 = 102 дням по ставке 30% годовых: t _г2= 30 + 25 - 1 = 54 дням.

Сумма начисленных процентов составит:

I = 300 000 = 64 500 руб.

2. При французской практике количество дней для начисле­ния процентов (табл. 7.1.1) по ставке 60% годовых равно:

t _ф1 = 12 + 30 + 31 + 31 + 1 - 1 = 104 дням;

Таблица 7.1.1

Дата добавления: 2014-12-27