Модели операций дисконтирования

Дисконтирование связано с распространенным в коммерчес­кой сфере утверждением «время - это тоже деньги», что обуслов­лено неравноценностью одинаковых по абсолютной величине сумм денежных средств сегодня и через некоторое время в будущем. Это объясняется, например, возможностью инвестировать капитал сегодня и в будущем получить доход. Кроме того, инфляционный процесс обесценивает денежную массу. Таким образом, можно ут­верждать, что «деньги сегодня» ценнее «будущих денег». Именно поэтому «золотое» правило бизнеса гласит: сумма, полученная се­годня, больше той же суммы, полученной завтра.

Дисконтирование позволяет учитывать в операциях фактор времени. Различают математическое дисконтирование и коммер­ческий или банковский учет.

Математическое дисконтирование связано с определением так называемого «современного» или «приведенного» значения Р на некоторый момент времени, которое соответствует заданно­му значению S в другой момент времени. Простейшая задача - определение суммы вклада Р на основе заданной конечной вели­чины в будущем S через временной период начислений n под за­данную, например, простую ставку процентов:

P = 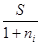= S·k _д,

где k _д - коэффициент дисконтирования (приведения) по простой ставке процентов k _д = .

Дисконтированное значение будущей суммы вклада по слож­ной ставке процентов равно:

P = = S·k _дс,

где k _дс - коэффициент дисконтирования (приведения) по сложной ставке процентов k _дс = ,

а по номинальной ставке процентов j при начислении процен­тов m раз в году -

P = .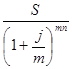

Банковский учет заключается в покупке денежных обяза­тельств, например, векселя банком по цене, которая меньше но­минальной указанной в нем суммы. В этом случае говорят, что вексель учитывается, и клиент получает сумму:

P = S - D,

где S - номинальная сумма данного обязательства;

Р - цена покупки векселя банком;

D - дисконт, сумма процентных денег (доход банка).

Процентный доход покупателя векселя банка может опреде­ляться по простой годовой учетной ставке:

d% = ·100%.

Если срок n от даты учета до даты погашения будет состав­лять часть года, то дисконт определяется по формуле

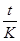D = n·d·S= ·d·S,

где d - относительная величина простой учетной ставки.

Предъявителю учитываемого денежного обязательства будет выдана сумма:

P = S - D = S (l - nd) = S .

Следует заметить, что дисконтирование может быть связано и с проведением кредитной операции. В таком случае проценты начисляются в начале интервала начисления, и заемщик полу­чает сумму Р за вычетом процентных денег D из суммы кредита S, подлежащего к возврату. Поэтому при проведении операции по простой учетной ставке d следует пользоваться формулой

S = ;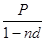

при проведении операции по сложной учетной ставке d _c -

S = ,

где d_c - относительная величина сложной учетной ставки.

Откуда можно найти другие показатели операции:

n = ; d_c = 1- .

Выгодность метода начисления процентов по учетной ставке для кредитора или заемщика зависит от величины процентной ставки и срока кредита.

В финансовых операциях используется и номинальная годо­вая учетная ставка /, по которой при начислении процентов m раз в году можно определить:

S =

Отсюда находим следующие формулы расчета показателей операции:

n = ; f = m .

При непрерывном начислении процентов по номинальной годовой учетной ставке f справедливо соотношение

S = = Pe^-f·n,

из которого находим следующие формулы:

n = ; f = ;

Пример 1. Финансовая компания выдает ссуду 15 000 руб. на полгода по простой годовой процентной ставке d = 5%. Опреде­лите сумму, которую получит клиент, и доход компании.

Решение. S = 15 000 руб.; d = 0,05; n = 0,5, тогда сумма, по­лученная клиентом, составит:

Р = S (l - nd) = 15 000(1 - 0,5 · 0,05) = 14 625 руб.

Доход финансовой компании исчисляется простым дискон­том, т.е. как процентный доход, вычитаемый из ссуды в момент ее выдачи:

D = ndS = 0,5 · 0,05 · 15000 = 375 руб.

Пример 2. Переводной вексель (тратта) выдан на 100 000 руб. с уплатой 12 ноября того же года. Владелец векселя учел его в банке досрочно - 12 сентября по простой учетной ставке 10%. Определите сумму, полученную владельцем векселя в банке, если число дней в году принять равным K = 360.

Решение. S = 10 000 руб.; d = 0,1; t = 60 дней; К = 360.

Находим сумму, полученную владельцем векселя:

P = l00000 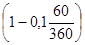= 98 333 руб. ЗЗ коп.

Пример 3. Дата погашения дисконтного векселя - 22 июля текущего года. Определите выкупную цену и дисконт на 2 июля векселя номиналом 100 млн. руб., если вексельная ставка состав­ляет 40% годовых, а число дней в году принять за 360.

Решение. S = 100 000 000 руб.; d = 0,4; t = 20 дней; К = 360.

Определяем выкупную цену дисконтного векселя:

P = S – D = S (1 - 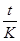d) = 100 000 000(1 - ) =
= 97 777 777 руб. 78 коп.

Пример 4. Операция, связанная с покупкой и последующей продажей облигаций, должна принести через 3 года прибыль в 100 000 руб. Определите современную ценность этой суммы по сложной годовой учетной ставке d = 30%.

Решение. S = 100000 руб.; d_c = 0,3; п = 3, тогда современная ценность суммы прибыли:

P = S (l - d_c)ⁿ= 100000(1 - 0,3)³ = 34 300 руб.

Пример 5. Клиент имеет вексель на 10 000 руб., который он хочет учесть 01.03.2000 в банке по сложной учетной ставке рав­ной 7%. Какую сумму он получит, если срок погашения векселя 01.08.2000?

Решение. Срок от даты учета до даты погашения векселя ра­вен:

t = 31 + 30 + 31 + 30 + 31 +1 -1 = 153 дням;

число дней в году К = 365 дней; S = 10 000 руб.; d_c = 0,07.

Клиент получит сумму:

P = S · (1 - d_c) = 10 000(1 - 0,07) = 9 700 руб. 38 коп.

Пример 6. Банк учитывает вексель за 2 года до срока его оп­латы по простой учетной ставке d = 6%. Какую сложную учет­ную ставку должен установить банк, чтобы доход банка остался прежним?

Решение. n = 2 года; d = 0,06.

Доход банка Д = S - Р. При применении простой учетной ставке d:

S = 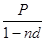; P = S (l – nd); Д = S·n·d.

При применении сложной учетной ставки d_c:

S = ; Р = S( 1 – d_c)ⁿ;Д = S

По условию доход должен быть одинаковым, поэтому долж­но выполняться соотношение:

S ·n·d = S ,

следовательно,

(l - d_c)² = l – 2 · d,

d_c = l - = 1 - = 0,062 = 6,2%,

т.е. сложная учетная ставка должна быть несколько больше, чем простая.

Пример 7. Банк учитывает вексель по номинальной учетной ставке f = 8% с начислением процентов 3 раза в году и желает перейти к сложной учетной ставке d_c. Какой величины должна быть ставка d_c, чтобы доход банка не изменился?

Решение. f = 0,08; т = 3.

Обозначим число лет за п. Чтобы доход не менялся, выдан­ная им сумма Р должна быть одинакова. В случае номинальной учетной ставки -

P = S .

В случае сложной учетной ставки -

P = S (1 - d_c)ⁿ.

Тогда запишем уравнение эквивалентности:

= (l - d_c)ⁿ,

1 - d_c = ,

откуда находим величину сложной учетной ставки

d_c = l - = l - = 0,078 = 7,8%,

которая будет меньше номинальной.

Дата добавления: 2014-12-27