Модели операций с облигациями

Облигация представляет собой долговую ценную бумагу, в соответствии с которой заемщик гарантирует кредитору выпла­ту по истечении определенного срока полной суммы долга с про­центами на определенную дату в будущем.

Эмитент выпускает облигации, на которых указаны их номи­нальная стоимость N и срок, по истечении которого облигации выкупаются (погашаются) эмитентом по номинальной стоимости.

Покупатель, приобретающий облигации по цене, меньшей номинала, предоставляет тем самым эмитенту ссуду и практичес­ки является кредитором. В таком случае покупатель получает доход, определяемый разностью между номиналом и ценой по­купки облигации и называемый дисконтом. Если к облигации прилагаются купоны, то, например, ежегодно или ежекварталь­но ему выплачиваются проценты по указанной на них ставке. Это является дополнительным так называемым купонным доходом.

Целью операций с облигациями является использование од­ного из вариантов финансовых вложений для получения дохода и тем самым обеспечение защиты от обесценения капитала и его роста в условиях инфляции.

При расчете доходности покупки облигаций используют по­нятие курса, определяемого ценой облигации, выраженной в про­центах от номинала:

P_k = ,

где Р - цена облигации;

N - номинальная стоимость облигации.

Цена облигации при заданном курсе определяется по форму­ле

P = .

Если по облигациям выплачиваются проценты, то облигации называются процентными, а доход по каждой выплате определя­ется от ее номинальной стоимости:

I = i_обл ·N.

Если проценты по облигациям не выплачиваются, то источни­ком дохода будет являться разность между ценой выкупа эмитен­том (по номиналу) и ценой покупки, которая называется дискон­том, такие облигации называются дисконтными, например государ­ственные краткосрочные обязательства (ГКО). Доход от этих обли­гаций находим как разность между номиналом и ценой покупки:

Д = N – P = N - 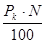= N (1 - 0,01 · P_k).

Доходность облигаций к погашению можно определить по эквивалентной ставке простых процентов:

i_э = .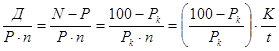

Доход от покупки долгосрочных облигаций с выплатой про­центов будет состоять из суммы полученных процентов и разни­цы между ценой их погашения (номиналом) и ценой покупки.

Если проценты по облигациям выплачиваются в конце года, на­пример, по ставке сложных процентов i _c, то сумма процентных денег при погашении облигации через n лет определяется по формуле

I = N (l + i_c)ⁿ – N = N ;

общий доход -

Д = I + N – P = N (l + i_c)ⁿ – P = N .

Доходность операции покупки-погашения облигации в виде эффективной ставки сложных процентов можно определить по формуле

S = P (1 + i_э)ⁿ, Д = S – P – P [(l + i_э)ⁿ -1].

На основе приведенных соотношений получим

i_сэ = = = .

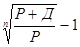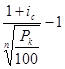При определении общего дохода следует учитывать возмож­ность реинвестирования, если проценты выплачиваются перио­дически.

Пример 1. Курс облигаций номиналом 500 руб. составляет 75. Определите цену облигации.

Решение. Р _к = 75; N = 500 руб.

Цена облигации равна:

P = 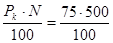= 375 руб.

Пример 2. Доход по облигациям номиналом 1000 руб. вып­лачивается каждые полгода по ставке 50% годовых. Вычислите сумму дохода по каждой выплате.

Решение. N = 1 000 руб.; I = 0,5; п = 0,5.

Сумма дохода по каждой выплате:

I = N·n·i = 1000 · 0,5 · 0,5 = 250 руб.

Пример 3. Облигации номиналом 1000 руб. и со сроком обра­щения 90 дней продаются по курсу 85. Определите сумму дохода от покупки 5 облигаций и доходность финансовой операции при расчетном количестве дней в году 360.

Решение. N = 1000 руб.; t = 90 дн.; К = 360; P_k = 85.

Доход от покупки одной облигации при условии ее погаше­ния составит

Д ₁ = 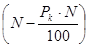= N = 150 руб.

Сумма дохода от покупки 5 облигаций составит

Д = 5 ·Д ₁= 5 · 150 = 750руб.

Доходность облигаций к погашению по эквивалентной став­ке простых процентов:

i_э = 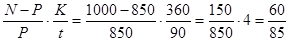= 0,706 = 70,6%.

Пример 4. Облигации номиналом 1000 руб. и сроком обра­щения 180 дней были приобретены в момент их выпуска по кур­су 65 и проданы через 90 дней по курсу 85. Определите доходность к погашению и текущую доходность в результате продажи для К = 360 дней.

Решение. N = 1000 руб.; t ₁= 180 дн.; ∆ t ₂ = 90 дн.; К = 360 дн.; P _k1 = 65; P _k2 = 85.

Доходность облигаций к погашению по эквивалентной став­ке простых процентов:

i_э = 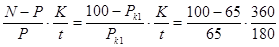= 1,077%

Текущая доходность в результате их продажи составит

i = .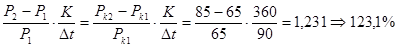

Пример 5. Облигация куплена по курсу 95 и будет погашена через 10 лет. Проценты по облигации выплачиваются в конце срока по сложной ставке 5% годовых. Определите доходность приобретения облигации.

Решение. Р_k = 95; q = 0,05; п = 10; Р = 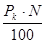= 0,95 N.

Процентный доход за 10 лет составит

I = N (1 + q) ^п - N = N [(1 + q) ⁿ - l] = N [(l + 0,05)ⁿ - l] = N [(l,05¹⁰ - l) = 0,629 N;

доход от помещения облигации -

Д _п = N (1 -0,0l P _k) = N (1 -0,95) = 0,05 N;

общий доход -

Д =I + Д _п= 0,629 N + 0,05 N = 0,679 N.

Доходность покупки облигации по эффективной ставке (сложных) процентов равна:

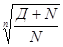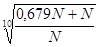i = -1 = - 1 = 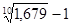= 1,053 – 1 = 0,053.

Пример 6. Банковская ставка по депозитам составит 10%, а банковская ставка по кредитам - 15%. Определите процент по облигациям, установленный при выпуске при условии, что их курс равен 98.

Решение. i ₁ = 0,1; i ₂ = 0,15; P_k = 98.

В качестве альтернативной ставки следует выбрать процент по депозитам, тогда процент по облигациям равен:

i_обл = 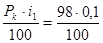= 0,098 = 9,8%

Пример 7. Банк А выдал банку Б межбанковский валютный кредит под залог облигаций внутреннего государственного ва­лютного займа третьего транша. Сумма кредита определяется путем оценки облигаций по текущей рыночной стоимости за вычетом из полученной суммы дисконта (в целях страхования от ценовых рисков).

Дата выдачи кредита Т ₀ - 30 октября; дата погашения кре­дита и процентов по нему Т ₁ - 13 ноября; процентная ставка по кредиту составляет 13% годовых на 360 дней в году; срок креди­та рассчитывается на основе полного количества календарных дней; сумма облигаций по номиналу 1 000 000 долл. США; курс облигаций - 81; размер дисконта - 10%. Банк Б попросил банк А погасить непогашенные купоны по облигациям за 1 год и произ­вести расчеты по полученному купонному доходу 13 ноября (на облигации ежегодно начисляется купонный доход из расчета 3% от номинала). За погашение купонов банк А возьмет комиссию в размере 1% от суммы купонного дохода. В день погашения кре­дита банки договорились оформить новый кредит под заложен­ные облигации с переоценкой облигаций по курсу 81,7. Стороны договорились произвести 13 ноября взаиморасчеты.

Определите, какой банк должен платить 13 ноября другому банку и какую сумму?

Решение. N = 1 000 000; i = 0,13; d = 0,1; Р ₀= 81; Р ₁ = 81,7; К = 360; i_обл = 0,03; q = 0,01.

Сумма S выданного кредита:

S = N · 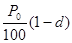= 1 000 000 · 0,81 · (1 - 0,1) = 729 000 долл.

Сумма процентов за кредит:

I = 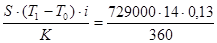= 3685,50 долл.

Сумма купонного дохода по облигациям:

Д_k = N· i_обл = 1 000 000·0,03 = 30 000 долл.

Комиссия за погашение купонного дохода:

C = Д_k q = 0,01·30 000 = 300 долл.

Сумма нового кредита:

S_н = N· = 1 000 000 · 0,817 · (1 - 0,1) = 735 300 долл.

Сведем взаимные требования сторон на 13 ноября в следую­щую таблицу.

Вид платежа	Банк А платит банку Б, долл.	Банк Б платит банку А, долл.
S		729000,00
I		3685,50
Дk	30000,00
C		300,00
Sн.	735300,00
Итого	765300,00	732985,50

В итоге 13 ноября банк А должен уплатить банку Б - 32 314,50 долл.

Пример 8. Брокеру фондовой биржи ММВБ поступило рас­поряжение 3 октября о размещении 2 млрд руб. на рынке ГКО при следующих условиях:

вложение денежных средств проводить только в краткосроч­ные выпуски (со сроком обращения менее полугода);

доля каждого выпуска в общем пакете должна занимать толь­ко часть объема капиталовложения и не превышать 30%;

продать весь пакет необходимо 4 ноября и вернуть деньги инвестору 5 ноября. На торгах 4 ноября по краткосрочным вы­пускам ГКО номиналом 1 млн руб. сложились следующие цены:

№ выпуска	Дата погашения	Цена, в % от номинала (курс)
	13.11.96	95,86
	20.11.96	95,00
	18.12.96	91,78
	03.01.97	89,44
	22.01.97	86,85

Сформируйте пакет ГКО исходя из условия получения мак­симальной доходности.

Рассчитайте средневзвешенную доходность пакета.

Выявите зависимость между доходностью ценной бумаги и сроком, оставшимся до ее погашения.

Решение. Под доходностью к погашению понимается доход, приносимый вложением в ценную бумагу с ожиданием ее пога­шения по номиналу.

Определяем доходность к погашению каждого выпуска в про­центах годовых:

i_э = ,

где 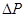- прирост в цене от текущего момента до погашения:

,

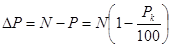где t _пог - количество дней до погашения;

К - количество дней в году, К = 360 дн.

Результаты расчетов представим в виде таблицы.

№ выпуска	Дней до погашения, t пог	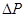, %	iэ, % годовых
		4,14	38,87
		5,00	40,31
		8,22	42,99
		10,56	46,71
		13,15	49,55

Из полученных результатов следует, что доходность ценной бумаги снижается с уменьшением срока, остающегося до ее пога­шения.

Исходя из требований инвестора необходимо перечислить по 600 млн руб. (30% от 2 млрд руб.) на покупку выпусков 21071, 21070, 21069, и на оставшиеся 200 млн руб. купить бумаги вы­пуска 21068.

Рассчитаем точное количество бумаг по каждому из приоб­ретаемых выпусков:

№ выпуска	Объем капиталовложений, руб.	Стоимость 1-й бумаги, руб.	Количество бумаг	Остаток от вложений, руб.
	600000000,00	868500,00		735000,00
	600000000,00	894400,00		752000,00
	600000000,00	917800,00		676600,00
	200000000,00	950000,00		500000,00

Просуммировав все остатки от вложений, получим 2663600,00 руб. свободных (невложенных) средств. Посколь­ку мы уже исчерпали 30% лимита по выпускам 21069—21071, следовательно, остаток средств надо потратить на покупку об­лигаций выпуска 21068. На оставшуюся сумму покупаем еще две бумаги данного выпуска, получая в остатке 763600,00 руб.

Окончательно сформированный пакет выглядит следующим образом:

№ выпуска	Количество бумаг, шт.	Объем капиталовложений
		5992650,00
		599248000,00
		599323400,00
		201400000,00
Свободные средства		763600,00

Подсчитаем средневзвешенную доходность к погашению по­лученного пакета ценных бумаг по следующей формуле:

= ,

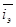где i_э1 - доходность к погашению первого выпуска;

V_i - объем вложений в первый выпуск;

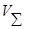- суммарный объем всех капиталовложений;

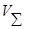= 2000000000,00 - 763600,00 = 1999236400,00 руб.

В результате подсчета получаем: 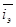= 45,80% годовых.

Пример 9. Утром 29 октября брокеру поступило распоряже­ние срочно продать, т.е. на сегодняшних торгах, весь пакет ГКО, сформированный по условиям примера 7,8, 29 ноября на торгах по краткосрочным выпускам ГКО сложились следующие цены (номинал каждой ценной бумаги - 1,0 млн руб.):

№ выпуска	Дата погашения	Цена, % от номинала (курс)
	13.11.96	98,53
	20.11.96	97,80
	18.12.96	94,86
	03.01.97	93,04
	22.01.97	90,22

В силу специфики расчетов на ММВБ и расчетов с инвесто­ром средства от реализации пакета поступят на счет инвестора на второй рабочий день от момента реализации.

Определите доход в рублях, полученный от вложения в ГКО, а также доходность в процентах годовых (из расчета 360 дней в году и полного количества дней в периоде) по данной финансо­вой операции с позиции инвестора.

Решение. Определяем сумму, полученную от реализации это­го пакета:

№ выпуска	Количество бумаг, шт.	Цена, в % от номинала	Общая сумма, руб.
		90,22	622518000,00
		93,04	623368000,00
		94,86	619435800,00
		97,80	207336000,00
Свободные средства	763600,00 руб.		763600,00
Итого	2073421400,00

Доход, полученный от вложения в ГКО, составляет:

Д = 2073421400,00 - 2000000000,00 = 73421400,00 руб.

Доходность определяется по формуле

i_э = ,

где Д - полученная прибыль;

Р - вложенная сумма;

- количество дней в периоде (необходимо рассчитывать количе­ство дней от 03.10 до 31.10, учитывая 2 дня, необходимые для передачи средств инвестору), т.е. = 28 дням;

К = 360 - количество дней в году.

i_э = = 47,2%

Дата добавления: 2014-12-27