
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Модели развития операций по схеме сложных процентов
|
|
|
|
В финансово-коммерческих операциях используется схема сложных процентов, если начисляемый процент (I) - (доход от капитала) суммируется с исходным капиталом (Р), и на следующем интервале начисления процент начисляется уже от всей образовавшийся суммы (Р + I). Этот вариант иногда называют капитализацией, или реинвестированием, или проценты на проценты. В этом случае сумма накопленного капитала составит:
к концу первого года:
S 1 = P + P · i c = P ·(l + i c),
где i c - относительная величина годовой ставки сложных ссудных процентов;
к концу второго года:
S 2 = S 1 + S 1. i c = S 1· (1 + i c) = P ·(1 + i c)2;
к концу третьего года:
S 3 = S 2 · (l + i c) = P· (l + ic) 3;
к концу n -го года:
S n = Р ·(1 + ic)n = Р · k нс,
где k нс - коэффициент наращения; k нс = (1 + ic)n.
Таким образом, накопление капитала по схеме сложных процентов образует возрастающую числовую последовательность: S 0, S 1, S 2, S 3,..., S n,которая представляет собой геометрическую прогрессию с первым членом b 0= S 0 - Р и знаменателем q = 1 + ic. В соответствии с этим можно записать формулу для определения любого ее члена:
Sn=b 0 - qn = P( l + ic) n.
Таким образом, получена модель наращения по формуле сложных процентов:
S = Р (1 + ic) n = Р (1 + ic) 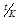 = Р · k нс,
= Р · k нс,
где t - срок контракта в днях;
k нс - коэффициент наращения.
Выводим формулы для определения таких показателей финансовой операции, как
величина первоначальной суммы -
P = 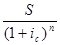 =
= 
(математическое дисконтирование при начислении сложных процентов);
относительная величина процентной ставки -
ic = 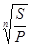 - 1
- 1
(одна из наиболее применяемых формул, используется для нахождения так называемой эффективной ставки сложных процентов, характеризующей доходность финансовой операции);
количество интервалов начисления (лет) -
n =  ;
;
период начисления процентов в днях -
t = K·  ;
;
продолжительность года в днях –
K =  ;
;
коэффициент наращения -
k нс = (1 + ic)n = (1 + ic) 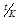 .
.
Если на протяжении всего срока контракта процентная ставка изменяется, то получим другую математическую модель определения наращенной суммы:
S = P (1 +iC  )n
)n  (1 +iC
(1 +iC 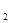 )n
)n 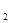 ... (1 +iC
... (1 +iC  )n
)n  … (1 +iC
… (1 +iC  )n
)n  = P
= P  n
n  ,
,
где nl - 1-й интервал начисления процентов, l =  ;
;
L - количество интервалов начисления;
k нс =  n
n  - коэффициент наращения.
- коэффициент наращения.
Начисление сложных процентов может осуществляться несколько раз в году: по месяцам, кварталам, полугодиям. В такихслучаях указывается ставка на периоде, а наращенная сумма находится по формуле
S = P ·(1 + i n)N,
где i n - ставка на периоде начисления;
N - количество интервалов начисления в течение срока действия контракта.
В случае когда начисление сложных процентов осуществляется через равные промежутки времени п, указывается номинальная годовая процентная ставка j, пользуются следующей формулой:
S = P 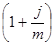 mn,
mn,
где т - количество интервалов начисления за год;
n - срок контракта в годах;
N = m·n - количество интервалов начисления за весь срок контракта.
На практике применяется еще и непрерывное начисление процентов по номинальной годовой процентной ставке j. В этом случае величину наращенной суммы находят из следующего выражения:
S = 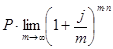 .
.
Затем при переходе к пределу при m  , используя известную формулировку второго замечательного предела:
, используя известную формулировку второго замечательного предела:
 = e,
= e,
получим такое уравнение:

следовательно, для определения наращенной суммы имеем формулу
S = Р·е 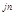 = Р· k нс,
= Р· k нс,
где k нс = е 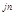 - коэффициент наращения при непрерывном начислении процентов по номинальной годовой ставке j.
- коэффициент наращения при непрерывном начислении процентов по номинальной годовой ставке j.
Приведенные модели позволяют проводить вычисления различных показателей финансовых операций.
Пример 1. Коммерческие банки С и D начисляют доход один раз в полгода, причем банк С по простой ставке, а банк D по сложной ставке процентов. Через год в этих банках средства инвестора увеличиваются на 60%. В какой банк выгоднее положить деньги на полгода и в какой - на полтора года?
Решение. По условию задачи коэффициенты наращения банков С и D равны, поэтому k н = k нс = 1,6, откуда для банка С ставка простых процентов определяется из выражения
k н =1 + ni = 1 + 2 i = 1,6 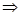 i =
i =  = 0,3 = 30%.
= 0,3 = 30%.
Для банка D ставка сложных процентов составляет
k нс = (1 + ni)2 = 1,6 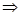 ic =
ic = 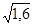 -1 = 0,265 = 26,5%.
-1 = 0,265 = 26,5%.
Следовательно, выгоднее положить деньги на полгода в банк С.
Для сравнения результатов финансовых операций с банками С и D можно составить следующую таблицу.
| t | 0,5 | 1,5 | 2,5 | 3,5 | ||||
| п | ||||||||
| k н | 1,3 | 1,6 | 1,9 | 2,2 | 2,5 | 2,8 | 3,1 | 3,4 |
| k нс | 1,265 | 1,6 | 2,02 | 2,56 | 3,24 | 4,1 | 5,18 | 6,56 |
Из данных таблицы следует, что на полтора года (как и вообще на любой срок свыше года) выгоднее положить деньги в банк D, поскольку k нс = 2,02 > k н = 1,9.
Пример 2. М. Е. Салтыков-Щедрин описывает в «Господах Головлевых» такую сцену: «Порфирий Владимирович... сидит у себя в кабинете, исписывая цифирными вкладками листы бумаги. На этот раз его занимает вопрос: сколько было бы у него теперь денег, если б маменька... подаренные ему при рождении дедушкой... на зубок сто рублей... не присвоила себе, а положила бы вкладом в ломбард на имя малолетнего Порфирия? Выходит, однако, немного: восемьсот рублей...»
Определите сложную ставку процентов годовых ломбарда по вкладам, если Порфирию в момент его расчетов было 50 лет.
Решение. п = 50; Р = 100 руб.; S = 800 руб.
По формуле сложных процентов наращенная сумма равна:
S = Р(1 + ic)n,
откуда ставка сложных процентов составит
ic =  =
=  = 0,0425
= 0,0425 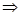 4,25%.
4,25%.
Пример 3. Знаменитый американский ученый и государственный деятель Бенджамин Франклин завещал жителям города Бостона 1 тыс. фунтов стерлингов на следующих условиях:
деньги давать под 5% годовых молодым ремесленникам;
через 100 лет из накопленных денег (с учетом процентов на проценты) 100 тыс. фунтов стерлингов пустить на строительство общественных зданий;
оставшиеся после этого деньги отдать под те же проценты еще на 100 лет;
по истечении этого срока накопленную сумму разделить между бостонскими жителями и правлением Массачусетской общины, которой передать 3 млн фунтов стерлингов.
Сколько денег должно было достаться бостонским жителям через 200 лет после смерти Б. Франклина (он умер в 1790 г.)?
Решение. Р = 1000 ф. ст., I с = 5%, п =100 лет.
1. Завещанный капитал через 100 лет составил:
S = 1000(1+0,05)100 = 131501 ф. ст.
2. После выделения 100 000 ф. ст. на постройку общественных зданий осталось:
131501 - 100000 - 31501 ф. ст.
3. Через 100 лет наращенный капитал составил:
S = 31501 ּ(1+0,05)100 = 4142 421 ф.ст.
4. Бостонским жителям из этой суммы после вычета 3 млн ф.ст. осталось:
4 142 421 - 3 000 000 - 1142 421 ф. ст.
Пример 4. Начисление процента на сумму срочного вклада с условием ежемесячной капитализации процентов.
Банк 20.07 заключает с вкладчиком договор срочного вклада на 3 месяца (срок возврата вклада - 20.10). Сумма вклада -15 тыс. руб. Процентная ставка - 22%. 20-го числа каждого месяца действия договора производится капитализация начисленных процентов. Переоформление вклада по окончании срока действия договора на ранее действовавших условиях срочного вклада договором не предусматривается. Выплата причисленных к сумме вклада процентов осуществляется по истечении срока действия договора.
В течение срока действия договора банк трижды - 20.08,20.09 и 20.10 производит капитализацию начисленных процентов во вклад. 20.10 - срок окончания договора срочного вклада, вкладчик не явился за вкладом в установленный договором срок. В этот же день после окончания операционного дня банк переоформляет указанный срочный вклад во вклад «до востребования».
Вкладчик 28.10 получает сумму вклада «до востребования» и начисления за период с 20.10 по 27.10 включительно (8 календарных дней) проценты по установленной ставке 4%.
Полный срок срочного вклада (20.07-20.10) - 93 календарных дня (n), период начисления процентов по ставке срочного вклада - 22% (20.07-19.10) - 92 календарных дня (n - 1).
Полный срок вклада до востребования (20.10-28.10) - 9 календарных дней (n), период начисления процентов по ставке вклада «до востребования» - 4% (20.10-27.10) - 8 календарных дней.
Порядок начисления банком процентов на сумму вклада:
сумма срочного вклада на 21.08 (с капитализацией процентов, начисленных за период с 20.07 по 19.08 включительно):
15000руб.+  = 15280руб.27коп;
= 15280руб.27коп;
сумма срочного вклада на 21.09 (с капитализацией процентов, начисленных за период с 20.08 по 19.09 включительно):
15280,27руб.+  = 15565руб.78коп;
= 15565руб.78коп;
сумма срочного вклада по состоянию на конец операционного дня 20.10 (с капитализацией процентов, начисленных за период с 20.09 по 19.10 включительно), в конце рабочего дня 20.10 и переоформленного во вклад «до востребования»:
15565,78руб.+ 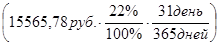 = 15856руб.63 коп.
= 15856руб.63 коп.
сумма начисленных на вклад «до востребования» процентов (за период с 20.10 по 27.10 включительно):
15 856,63 руб.·  = 13 руб.90 коп.
= 13 руб.90 коп.
Таким образом, общая сумма возврата денежных средств вкладчику составит на 28.1015870 руб. 53 коп., из которых 15856 руб. 63 коп. - сумма срочного вклада с учетом капитализированных процентов и 13 руб. 90 коп. - проценты, начисленные за время, прошедшее с момента переоформления указанного срочного вклада во вклад «до востребования».
Пример 5. Начисление процентов на сумму срочного вклада по формуле сложных процентов.
Банк 05.09 заключает с вкладчиком договор срочного банковского вклада на 21 день (срок возврата вклада - 26.08). Сумма вклада - 15 тыс. руб. Процентная ставка - 15%. По условиям договора начисленные по итогам каждого дня срока действия депозита проценты увеличивают сумму вклада.
Полный срок вклада (05.08-26.08) - 22 календарных дня (n), период начисления процентов по вкладу (05.08-25.08) - 21 календарный день (п - 1).
26.08 банк возвращает вкладчику вклад (с учетом ежедневной капитализации процентов) в сумме:
15000руб.· 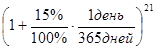 = 15129руб.99коп.
= 15129руб.99коп.
Пример 6. Банк выдал коммерческому предприятию 16.08 валютный кредит под контракт на покупку товаров, на сумму 10 000 долл. США, срок кредита 2 месяца (до 16.10); ставка процентов - 35% годовых за полное количество календарных дней из расчета 360 дней в году, при подсчете количества дней в периоде граничные дни (первый и последний) считаются за 1 день; порядок выплаты кредита: 16.09 - проценты за первый месяц, 16.10 - проценты за второй месяц и сумма кредита; штрафные санкции по ставке сложных процентов составляют 0,5% от просроченных сумм кредита за каждый день просрочки. Очередность погашения просроченной задолженности: в первую очередь погашаются начисленные штрафы, затем сумма процентов и сумма кредита.
Фактически 16.09 клиент погасил проценты за первый месяц кредита. Далее кредит погашался в следующей последовательности: 22.10 клиент перевел 2600 долл. США в счет погашения задолженности; 25.10 клиент перевел 3100 долл. США в счет погашения задолженности, а 30.10 клиент заявил, что готов погасить свою задолженность в полном объеме.
Определите величину задолженности клиента на 30.10.
Решение. Определяем:
сумму задолженности на 16.10 -
S 1 = P (1 + i · n) = l0000  = 10291,67 долл.;
= 10291,67 долл.;
сумму задолженности на 22.10 до внесения первой суммы на погашение -
S 2 = 10291,66+10000 · 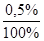 ·6 =10591,66 долл.
·6 =10591,66 долл.
После частичного погашения сумма долга составит -
S  = S 2 - 2600 = 10591,66 - 2600 = 7991,66 долл.
= S 2 - 2600 = 10591,66 - 2600 = 7991,66 долл.
Рассчитаем сумму задолженности S 3 на 25.10 до внесения второй суммы на погашение -
S 3 = 7 991,66· 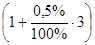 = 8111,53 долл.
= 8111,53 долл.
После частичного погашения долга сумма долга составит
S 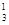 =S 3 - 3100 = 8111,53- 3100 = 5 011,53 долл.
=S 3 - 3100 = 8111,53- 3100 = 5 011,53 долл.
Определяем сумму задолженности S 4 на 30.10 -
S 4 = S 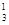
 = 5011,53 ·1,025 = 5136.82 долл.
= 5011,53 ·1,025 = 5136.82 долл.
Следовательно, на 30 октября полная задолженность по кредиту, процентам и начисленным штрафам составит 5136,82 долл. США.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 1487; Нарушение авторских прав?; Мы поможем в написании вашей работы!