Модели сравнения финансово-коммерческих операций

Для выбора из различных схем финансово-коммерческой опе­рации наиболее выгодной необходимо проводить их сравнение с наиболее выгодной схемой финансовой или коммерческой опера­ции. Юридические или физические лица, участвующие в опера­ции (сделке), должны ясно представлять ее результаты, оценить выгоду, определить доходность или эффективность операции.

Простейшим видом финансово-коммерческой операции явля­ется однократное предоставление кредитором в долг товара на сум­му или суммы Р заемщику (дебитору) с условием, что через неко­торое время п будет возвращена сумма S. Для оценки эффективно­сти такой операции можно использовать следующие показатели:

относительный рост, относительную величину ставки процен­та, называемую интересом:

i = ;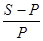

относительную скидку, или дисконт:

d = .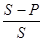

Эти показатели характеризуют приращение капитала креди­тора, отнесенное либо к первоначальной сумме (интерес), либо к конечной сумме (дисконт).

Между этими показателями существует связь, которая нахо­дится путем совместного решения этих уравнений, откуда мож­но получить следующие модели:

i = 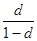; d = .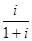

В операциях иногда вместо дисконта используют дисконт-фактор, определяемый по такой формуле

V = 1 – d = .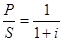

Для определения выгодности операции используют сравни­тельную доходность, которая на основе допущения о равенстве финансовых результатов различных вариантов проведения опе­раций приводит к понятию эквивалентных процентных ставок простых или сложных процентов. Это позволяет получить инст­румент корректного сравнения операций.

Эквивалентные ставки дают одинаковые финансовые ре­зультаты или наращенные суммы S при равных промежутках времени n.

Для этих целей используют базовые модели вычисления на­ращенных сумм реальных процентных ставок:

S = P (1 + ni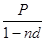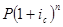), S = ,

S = 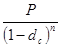, S = ,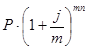

S = , S = .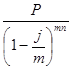

На этом основании можно в обобщенном виде написать моде­ли связи возможных вариантов сочетания эквивалентных ставок (30 формул):

эквивалентные ставки простых процентов -

i _э = φ(i _c), i _э = φ(j), i _э = φ(d), i _э = φ(d _c), i _э = φ (f);

эквивалентные ставки сложных процентов -

i _сэ = φ(i), i _сэ = φ(j), i _сэ = φ(d), i _сэ = φ(d _c), i _сэ = φ(f);

эквивалентные номинальные ставки сложных процентов -

j_э = φ(i), j_э = φ (i _c). j_э = φ(d), j_э = φ (d _c), j_э = φ(f);

эквивалентные простые учетные ставки процентов -

d _э = φ(i), d _э = φ(i _c), d _э = φ(j), d _э = f (d _c), d _э = φ(f);

эквивалентные сложные учетные ставки процентов -

d _сэ= φ(i), d _сэ = φ(i _c), d _сэ= φ(j), d _сэ= φ(d), d _сэ= φ(f);

эквивалентные номинальные сложные учетные ставки про­центов -

f _э = φ(i), f _э = φ(i _c), f _э = φ(j), f _э = f (d), f _э = φ(d _c).

Для нахождения эквивалентных ставок составляют уравне­ния эквивалентности по следующим правилам. Рассматривается результат инвестирования капитала Р на срок п лет:

S = Р + Д,

где Д - доход.

Эту операцию можно сопоставить с эквивалентной операци­ей вложения средств, например, по ставке простых процентов i _э. Тогда сумма вложенных средств с процентами будет равна:

S = P· (1 + n i _э).

Доход по этой операции составит

Д = S – Р = Р · n · i _э = Р· i _э· ,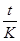

где t - срок операции в днях.

Следовательно, эквивалентная ставка простых процентов будет равна:

i _э = .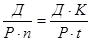

При учете денежных обязательств, например, векселей с ис­пользованием учетной ставки доход (дисконт) определяется фор­мулой

D = n·d·S = S - P,

откуда эквивалентная ставка простых процентов будет рав­на:

i _э = .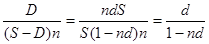

На основе равенства двух выражений можно составить урав­нения эквивалентности для других сочетаний различных вариан­тов процентных ставок. Так, например, приравнивая наращенные суммы при схемах начисления простых и сложных процентов:

S = P (l + ni); S = P (l + i _c)ⁿ,

получим следующее уравнение эквивалентности:

P (l + ni) = P (l + i _c)ⁿ,

из которого следует определение эквивалентной ставки простых процентов

i _э = ,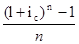

или эквивалентной ставки сложных процентов

i _сэ = 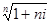- 1.

При начислении сложных процентов получаем следующее уравнение эквивалентности:

(l + i _c)ⁿ = ,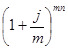

откуда получим эквивалентную годовую ставку сложных процентов:

i _сэ = 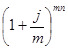- 1,

которая определяет так называемую годовую эффективную ставку сложных процентов, эквивалентную номинальной сложной процентной ставке, и не зависит от срока операции n. Эффектив­ная ставка сложных процентов, эквивалентная сложной учетной ставке, равна:.

i _сэ = ,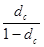

а эквивалентная - номинальной сложной учетной процентной ставке -

i _сэ = .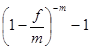

Эти показатели необходимы для оценки реальной доходности финансовых операций или для сравнения различных процентных ставок, что в конечном итоге позволяет вычислить доходность и аргументировать выбор варианта для инвестирования капитала.

Пример 1. Кредит на 2 года получен под 60%-ную номиналь­ную ставку сложных процентов. Начисление происходит ежек­вартально. Оцените эффективность операции через эквивалент­ные простую и сложную ставки процентов.

Решение. j = 0,6; n = 2; т = 4.

Эквивалентная ставка простых процентов равна:

P (1 + i·n) = P 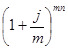, 1 + i·n = ,

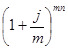i = 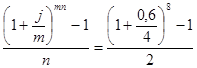= 1,03; i% = 103%

эквивалентная эффективная ставка сложных процентов -

P (l + i _c)ⁿ = P 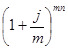; i _c = 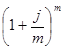- 1 = 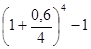= 0,749;

i _c = 74,9%

Пример 2. Определите, под какую простую ставку процентов выгоднее поместить капитал на 1 год: с ежемесячным начисле­нием 40%, с ежеквартальным начислением 120% или с ежегод­ным начислением 1000%.

Решение. Доходность вариантов сравниваем по величине го­довых ставок простых процентов:

i ₁= 40% ·12 = 480%,

i ₂= 120% · 4 = 480%,

i ₃= 1000%,

очевидно i ₃ > i ₁ = i ₂

Следует заметить, что приведенные данные были в реальной ситуации на фондовом рынке, и, как правило, по третьему вари­анту вкладчики так ничего и не получили (даже своего вклада), а вот по первому варианту, используя реинвестирование по трех­месячным контрактам, они получили финансовый результат, пре­вышающий третий вариант.

Пример 3. Срок оплаты долгового обязательства составляет полгода по простой учетной ставке 40%. Оцените доходность опе­рации по эквивалентным ставкам (считать, что номинальная став­ка начисляется ежеквартально).

Решение. d = 0,4; п = 0,5; т = 4.

Эквивалентная простая ставка ссудного процента равна:

1 + ni =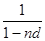

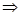
i ₁ = 40% ·12 = 480%;

i = 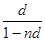= = 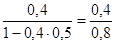0,5 i % = 50%

эквивалентная ставка сложного процента -

(l + i _c)ⁿ =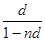

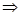
i _c = 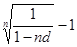= = 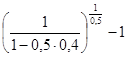= 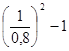0,5625

i _c % = 56,25%

эквивалентная номинальная ставка сложного процента -

=

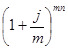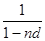
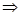
j = m 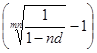= 4 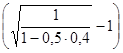= 0,472

j % = 47,2%

эквивалентная сложная учетная ставка -

=

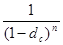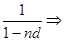
d_c = l - 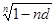= l - (1 - 0,5 · 0,4)² = 1 - 0,64 = 0,36;

d _c% = 36%;

эквивалентная номинальная учетная ставка -

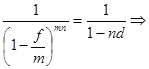
f = m (l - 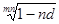) = 4(1 - 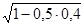) = 0,422;

f % = 42,2%.

Дата добавления: 2014-12-27