Модели финансовых и товарных потоков

Финансовые и товарные потоки являются составной и неотъемлемой частью практически любой сферы человеческой де­ятельности. В коммерции они образуют питательную среду това­родвижения. В экономической, финансовой, производственной и других сферах, направленных на удовлетворение потребностей человека, эти потоки порождают интерес и объясняют смысл их существования. Примерами таких потоков являются: оплата по заключенным договорам, которая может предусматривать как ра­зовый платеж, так и ряд выплат, распределенных во времени; по­гашение банковской задолженности или коммерческого кредита частями и т.п. При этом может возникать целый ряд последова­тельных, например равновеликих, платежей R, которые и обра­зуют поток платежей в соответствии с контрактами на поставку товаров.

При некоторых платежах проценты начисляются на нахо­дящиеся в обороте деньги. Здесь возникают две основные задачи: определить наращенную сумму потока платежей или, наоборот, по наращенной сумме определить величину отдельного платежа. Очевидно, в контрактах на поставку товаров это необходимо учи­тывать во взаимозачетах.

Ряд последовательных финансовых платежей, производимых через равные промежутки времени, называются финансовой рен­той, или аннуитетом. Это - частный случай потока платежей, все члены которого - положительные величины. Примерами аннуи­тета могут быть регулярные взносы в пенсионный или другие фонды, выплаты процентов по ценным бумагам, например по акциям, платежи за партии товаров и т.д. Финансовая рента име­ет следующие основные характеристики: член ренты R_j - вели­чина каждого отдельного платежа; интервал ренты τ_j - времен­ной интервал между двумя платежами; срок ренты t - время от начала реализации ренты до момента последнего платежа (быва­ют и вечные ренты); процентная ставка для расчета наращения или дисконтирования платежей; S - наращенная будущая сумма ренты, включающая все члены потока платежей с процентами на дату последней выплаты; современная (приведенная) величина ренты А - сумма всех членов потока платежей, дисконтирован­ная (уменьшенная) на величину учетной ставки на начальный момент времени ренты.

Ренты подразделяются на постоянные, когда члены ренты равны: R ₁= R ₂ = R ₃=... = R _n, и переменные.

По моменту выплат членов ренты различают ренты: постну-мерандо (обычные), в которых платежи осуществляются в конце соответствующих периодов, и пренумерандо, в которых платежи производят в начале указанных периодов.

Рассмотрим модели потоков ежегодных платежей, с начис­лением процентов на платежи в конце каждого года (постнумерандо) по сложной процентной ставке.

Сумма первого платежа S _lснаращенными на него за весь срок процентами определяем из уравнения

S _l = R· (l + i_c)^n-1,

где n - количество платежей величиной R.

Для второго платежа, для которого проценты начисляются на один год меньше, соответственно получим

S ₂ = R· (l + i_c)^n-2.

Для третьего платежа наращенная сумма составит

S ₃ = R· (l + i_c)^n-3.

На последний платеж, произведенный в конце последнего п- го года, проценты не начисляются:

S_n = R· (l + i_c)^n-n = R.

Тогда для вcей наращенной суммы ренты получим

S = 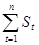= = 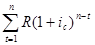R .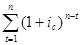

Коэффициент наращения равен:

k _на= .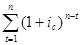

Следует заметить, что этот коэффициент представляет собой сумму членов геометрической прогрессии, где первый член ра­вен b ₁= 1, а знаменатель q = (1 + i _c) > 1. На этом основании, ис­пользуя формулу для суммы членов геометрической прогрессии, преобразуем полученное выражение для наращенной суммы рен­ты к такому виду

S = R ,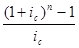

из которой следует, что коэффициент наращения можно оп­ределить таким выражением:

k _на = .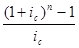

Для каждого платежа современное значение определяется формулой

A_t = R .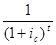

Современная приведенная величина всей ренты будет опре­деляться выражением

A = 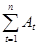= R 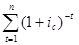= a·R,

где а является коэффициентом приведения ренты и определяется фор­мулой для суммы геометрической прогрессии с параметрами

b ₁ = 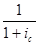, q = ,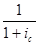

в соответствии с которой находим

a = = .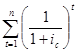

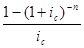Следовательно, получим выражение для приведенной вели­чины ренты

A = R .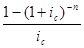

Полученные модели позволяют определить, например, вели­чину платежа

R = =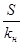

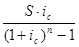
или

R = = .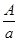

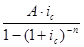Для определения срока ренты можно получить следующие формулы:

n = 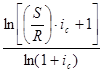, n = - .

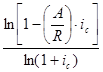В зависимости от исходных данных при решении каждой за­дачи формируется соответствующий набор моделей для опреде­ления количественных значений показателей контракта.

Пример 1. Вкладчик в конце каждого месяца вкладывает в банк 1000 руб. Проценты начисляются ежемесячно по номиналь­ной годовой ставке сложных процентов, составляющей 12%. Оп­ределите наращенную сумму на счете вкладчика через 2 года.

Решение. R = 1000; n = 24; m = 12; i = = = 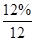1% = 0,01.

S = R · 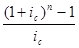= 1000· 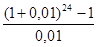= 10^{5 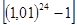=} l00000· =

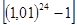= 100000·(l,2697346 - l)= 26973руб.46коп.

Если бы вкладчик накапливал долг и ие включал в оборот, то наращенная сумма составила бы всего 24 000 руб.

Другая задача, обратная этой, заключается в вычислении ре­гулярных платежей финансовой ренты R по заданной наращен­ной сумме.

Пример 2. Вкладчик желает накопить в течение двух лет в банке 30 000 руб., производя ежемесячные равные вклады по сложной номинальной годовой ставке 12%. Определите сумму ежемесячного вклада при условии, что проценты начисляются ежемесячно.

Решение. S = 30000; п = 24; j = 12%; i_c = 0,01.

Сумма ежемесячного вклада составит

R = 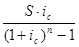= = 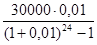= 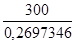1112 руб. 20 коп.

Пример 3. Вкладчик намерен положить в банк сумму, чтобы его сын в течение пятилетнего срока обучения мог снимать в кон­це каждого года по 10 000 руб. и израсходовать к концу учебы весь вклад. Определите сумму вклада, если годовая ставка слож­ных процентов -12%.

Решение. Сумма вклада равна современной ценности ренты, состоящей из пяти платежей:

A = R· 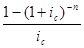= 10000· = = =

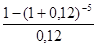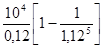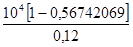= 36047 руб. 76 коп.

Пример 4. Заемщик получил кредит 3 млн руб. на 5 месяцев с условием гашения долга в конце каждого месяца равными срочны­ми платежами. На величину долга начисляются сложные процен­ты по ставке 5% за месяц. Определите сумму срочного платежа.

Решение. п = 5; А = 3 000 000 руб.; i_с = 0,05.

Сумма срочного платежа

R = 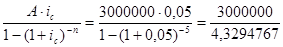= 692924 руб. 39 коп.

Дата добавления: 2014-12-27