Модели операций с акциями

Акция представляет собой долевую ценную бумагу, в кото­рой указывается непосредственная доля держателя акции в ре­альной собственности и обеспечивает получение дивиденда. В зависимости от порядка начисления и выплаты дивидендов ак­ции делят на привилегированные и обыкновенные.

Дивиденды по привилегированным акциям объявляются в фиксированных процентах от номинальной ее стоимости N и оп­ределяются по формуле

D ₁ = f · N

где f - годовая ставка дивиденда.

Доход на одну обыкновенную акцию равен:

Д ₀ = ,

где М ₀ - количество обыкновенных акций;

ЧП - распределяемая чистая прибыль;

D _пр - дивиденд по всем привилегированным акциям

D _пр= М _пр · D ₁;

М _пр - количество привилегированных акций.

Обычно на выплату дивидендов по обыкновенным акциям может идти не весь доход, а только его часть, поэтому величина выплачиваемого дивиденда определяется дивидендным выходом:

D _вых = ,

где D ₀ - дивиденд на одну обыкновенную акцию.

Доходность по акциям определяется доходом от выплачива­емых дивидендов, а также разницей в цене покупки и продажи, что и определяет эффективность инвестиций:

Э = ,

где Р_a - цена покупки;

P ₁ - цена продажи;

D - дивиденды за время владения акцией.

Для проведения анализа операций с акциями необходимо проводить расчеты по нескольким показателям.

Доходность текущая, без учета налогообложения, определя­ется по формуле

i _T = ,

где Р_а - курсовая стоимость акции.

Курсовая стоимость акции определяется в сравнении с бан­ковской депозитной ставкой i:

Р_а = .

Доходность конечная определяется суммой дивидендов и до­полнительным доходом от перепродажи:

i_э = .

Доходность текущая, с учетом налогообложения, определя­ется выражением:

i _тн = ,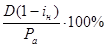

где i _н - ставка налогообложения.

Курсовая стоимость определяется и от номинальной цены акции:

P_a = .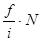

Рыночная цена акций определяется спросом и в связи с этим находится показатель ценности акций на рынке:

.

При долгосрочных операциях с акциями можно применять формулы определения эквивалентных ставок простых и сложных процентов:

S = P (1 + ni_э); S = P (1 + ni_э) ⁿ.

Доход от финансовых операций в таких случаях определяет­ся так:

Д = S – P = ni_эP; Д = Р [(1 + i_э)ⁿ -1],

откуда исчисляются эквивалентные ставки простых и слож­ных процентов:

i_э = ; i_cэ = .

Пользуясь приведенными моделями, можно проводить срав­нение выгодности финансовых операций с акциями и, следова­тельно, решать задачу выбора оптимального инвестиционного проекта.

Пример 1. Банк объявил, что дивиденды по его акциям за прошедший год составляют 20% годовых по обыкновенным ак­циям и 30% годовых по привилегированным. Определите сумму дивиденда на одну привилегированную акцию номиналом 3000 руб. и одну обыкновенную акцию номиналом 1000 руб.

Решение. Сумма дивиденда на одну привилегированную ак­цию равна: D_пр = 0,3 - 3000 - 900 руб.;

сумма дивиденда на одну обыкновенную акцию - D₀ = 0,2 ·1000 = 200 руб.

Пример 2. Определите ожидаемый доход от покупки акции номиналом 1000 руб., от ежегодного получения дивидендов в раз­мере 20% годовых и ежегодного роста стоимости на 10% от но­минала, если акция будет продана через 5 лет, а также доходность операции.

Решение. N = 1000 руб.; f = 0,2; n = 5 лет; ∆ Р ₁ = 0,1 N. Величина годовых дивидендов за 5 лет составит:

Д = n·f·N = 5 · 0,2 ·1000 руб.

Стоимость акции через 5 лет -

Р_а = N + 0,1 · N · 5 = N (1 + 0,5) = 1500 руб.;

общий доход -

Д_a = D + P_a – N = 1000 + 1500 - 1000 = 1500 руб.

Доходность покупки акции в виде эквивалентной ставки сложных процентов составит:

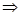= 1,201 – 1 = 0,201 20,1%

Пример 3. АО с уставным фондом 1 млн руб. имеет следую­щую структуру капитала: 85 обыкновенных акций и 15 привиле­гированных. Размер прибыли к распределению между акционе­рами составляет 120 тыс. руб. Фиксированный дивиденд по при­вилегированным акциям составляет 10%. Определите дивиден­ды для владельца обыкновенной акции.

Решение. ЧП = 120000 руб., М ₀ = 85, М _пр = 15, УК = 100000 руб., f = 0,1.

Номинал одной акции находим как отношение уставного фонда к общему числу акций:

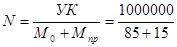10000 руб.;

выплаты но всем привилегированным акциям равны:

Д _пр = М _пр Д ₁ = N ·15· f = 10000 · 15 · 0,1 = 15000руб.;

выплаты на одну обыкновенную акцию -

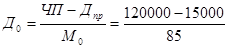= 1235 руб. 29 коп.

Пример 4. Балансовая прибыль АО с уставным фондом 2 млн руб., полученная от производственной деятельности, составила 10 млн руб. Собрание акционеров постановило, что оставшуюся после уплаты налогов прибыль следует распределить так: 20% на развитие производства, а 80% - на выплату дивидендов. Оп­ределите курс акций, если банковский процент составляет 80%, номинал акции -100 руб., а ставки налога на прибыль - 32%.

Решение. УК = 2 000 000 руб., БП = 1 000 000 руб., Д_вых = 0,8; i = 0,8; N =100 руб., W = 0,32.

Количество акций АО равно:

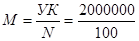= 20 000 шт.;

прибыль после уплаты налогов составит:

ЧП = БП (1 - W)= 10 000 000 · (1 - 0,32) = 6 800 000 руб. - 6,8 млн руб.;

величина дивидендов на выплату акционерам -

= 6800 000 · 0,8 = 5 440 000 руб.;

выплата дивидендов на одну акцию -

;

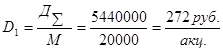курс акции составляет:

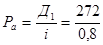= 340 руб.

Рассмотрим пример, связанный с финансами предприятий, иллюстрирующий как по данным бухгалтерской отчетности пред­приятия можно рассчитать его реальную стоимость и стоимость одной акции.

Пример 5. Рассчитайте реальную стоимость предприятия на 01.07, а также стоимость одной акции АО «Дорстрой» номина­лом N = 50 руб. на основе следующих данных:

уставный капитал У_k = 2115 тыс. руб.;

активы по балансу предприятия А_k = 3000475 тыс. руб.;

непроизводственные основные средства других отраслей H _с = 43266 тыс. руб.; балансовая прибыль за отчетный период БП = 99115 тыс. руб.;

начисленная за период амортизация А_м = 4328 тыс. руб.;

платежи в бюджет за отчетный период ПБ = 34690,2 тыс. руб.;

средства, направленные на погашение кредитов и уплату процентов по ним Кр = 9700 тыс. руб.;

норма дисконта d = 0,2;

кредиты и другие заемные средства КЗ = 515904 тыс. руб.;

убытки (по балансу) У = 112531 тыс. руб.;

курс доллара на дату баланса К _д= 5115 руб. на 01.07.96 г.;

средний курс доллара США за период К _с= 4856 руб.;

коэффициент риска (учитывающий нефинансовые критерии) К = 0,2.

Решение. Балансовая оценка стоимости имущества предпри­ятия (без учета задолженности):

БС = 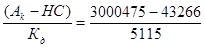= 578,14 тыс.долл.

Оценим стоимость предприятия по методу будущей доходно­сти:

денежный поток за анализируемый период составит

Д _п = (БП + А _м - ПБ - Кр) · Кс = (99115 + 4328 - 34 690,2 - 9 700) · 4856 =

= 12,16 тыс. долл.;

годовой денежный поток -

= Д _п · 2 = 12,16·2 = 24,32 долл.;

стоимость предприятия -

С _д = 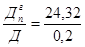= 121,61 тыс. долл.

Рассчитаем максимальную среднюю стоимость предприятия:

= 349,88 тыс. долл.;

задолженность предприятия -

З = 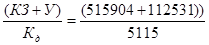= 122,86 тыс. долл.;

максимальную стоимость предприятия за вычетом задолженности-

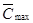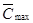= - З = 349,88 - 122,86 = 227,02 тыс. долл.;

стоимость предприятия по состоянию на 01.07 -

С = 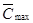· К = 227,02 · 0,2 = 45,4 тыс. долл.;

стоимость одной акции предприятия на 01.07 -

= 1,07 долл.

Таким образом, стоимость АО «Дорстрой» составляет 45,4 тыс. долл., а стоимость одной акции АО номиналом 50 руб. -1,07 долл.

Контрольные вопросы

1. Каково содержание финансово-коммерческой операции?

2. Каковы показатели финансово-коммерческой операции?

3. Приведите пример механизма развития финансово-коммер­ческой операции по схеме простых процентов.

4. Каков механизм развития коммерческих операций по схеме сложных процентов?

5. Как следует учитывать инфляцию в коммерческих опера­циях?

6. Как можно использовать вексель в коммерческих операциях?

7. Поясните на моделях утверждение коммерческой сферы: сумма, полученная сегодня, больше той же суммы, полу­ченной завтра.

8. Как следует сравнивать финансово-коммерческие опера­ции?

9. Каким образом можно использовать операции с ценными бумагами в коммерческом деле?

Дата добавления: 2014-12-27