Абсолютная и относительная погрешность

Оценки погрешности округления.

IV. Вычислительная погрешность.

III. Погрешность метода.

II. Неустранимая погрешность.

Выбрав определенную модель, мы неизбежно сталкиваемся с тем, что различные параметры, входящие в уравнение модели, а также начальные данные заданы с некоторой погрешностью, которая получается в результате экспериментов и измерений. Так, в рассмотренном примере это касается параметров l, g, µ, начального положения маятника и др. Погрешность такого рода называется неустранимой, так как она не может быть уменьшена в процессе численного решения. Ее уточнение возможно лишь за счет более точного определения параметров задачи.

В большинстве случаев исследуемые уравнения, в частности, уравнение (2), не могут быть решены аналитически и для их решения используют тот или иной приближенный численный метод. При этом возникает погрешность метода, являющаяся одной из важнейших характеристик любого частного алгоритма.

Так как количество разрядов записи числа на бумаге и в ЭВМ, конечно, то при выполнении арифметических и более сложных операций, приводящих к увеличению количества разрядов, приходится производить округления результатов, что приводит к появлению вычислительной погрешности, которую еще называют погрешностью округления.

Замечание. Полная погрешность решения, то есть разность между реально получаемым и точным решением задачи, не превосходит суммарного значения четырех рассмотренных погрешностей.

Рассмотрим способы оценки вычислительной погрешности.

Определение 1. Величина Δ_а = | А – а |, где А – точное значение числа, а а – его приближенное значение, называется абсолютной погрешностью числа а.

Например, если А = 2,1463 и а = 2,15, то абсолютная погрешность числа а будет равна Δ_а = | А – а | = |2,1463 – 2,15| = 0,0037.

На практике значение абсолютной погрешности Δ_а, как правило, невозможно вычислить, так как точное значение А в подавляющем числе случаев неизвестно, а значит невозможно найти разность А – а. Поэтому для оценки абсолютной погрешности рассматривают наименьшее число Δ, удовлетворяющее условию

| А – а | ≤ Δ. (3)

Число Δ, удовлетворяющее условию (3), называется предельным значением (границей) абсолютной погрешности Δ_а. Из неравенства (3) следует, что

а – Δ ≤ А ≤ а + Δ. (4)

Например, запись А = 2,21 ± 0,01 означает, что точное значение А, удовлетворяет условию 2,21 – 0,01 ≤ А ≤ 2,21 + 0,01 или 2,2 ≤ А ≤ 2,22.

Замечание. Если а – приближенное значение числа А, причем предельная абсолютная погрешность равна Δ, то говорят, что а есть приближенное значение числа А с точность до Δ.

Пример 1. Пусть точное значение А некоторого числа находится в интервале А₁ ≤ А ≤ А₂, а его приближенное значение а равно полусумме 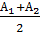, т.е. а = 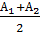. Найти предельную абсолютную погрешность.

Дата добавления: 2014-12-27