
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Упражнения. 1.1 Найти предельную абсолютную погрешность приближенного значения: а) а = 1,415 числа ; б) а = 2,7185 числа ; в) а = 1,735 числа ; г) а
|
|
|
|
1.1 Найти предельную абсолютную погрешность приближенного значения: а) а = 1,415 числа 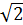 ; б) а = 2,7185 числа
; б) а = 2,7185 числа  ; в) а = 1,735 числа
; в) а = 1,735 числа 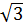 ; г) а = 2,25 числа
; г) а = 2,25 числа  .
.
1.2 В результате измерения получены приближенные значения величин: x = 34,8 ( 0,2); y = 0,00464 (
0,2); y = 0,00464 ( 0,00004); z = 4327 (
0,00004); z = 4327 ( 30). Найдите предельную относительную погрешность каждого из данных чисел.
30). Найдите предельную относительную погрешность каждого из данных чисел.
1.3 1) Округлить число 0,350264: а) до четырех значащих цифр; б) до двух значащих цифр.
2) Округлить число −15,502615: а) до пяти значащих цифр; б) до двух значащих цифр; в) до семи значащих цифр.
3) Округлить число 150,0571: а) до четырех значащих цифр; б) до двух значащих цифр; в) до пяти значащих цифр.
1.4 Округлить число: а) −10,55 до десятых; б) 2,30618 до сотых; в) 0,05029725 до десятитысячных; г) −150,40289 до единиц. Найти абсолютную и относительную погрешности округления.
1.5 Определить верная или сомнительная последняя значащая цифра в приближенном числе а, если а) А = 0,352, а = 0,35; б) А = 0,352, а = 0,36; в) А = −1,256, а = −1,3; г) А = 12,5029, а = 12; д) А = −7,0127, а = −7,013; е) А = 2,5387, а = 3.
1.6 Найти предельные абсолютные погрешности и относительные погрешности приближенных чисел, записанных в десятичной форме верными цифрами: а = 3,14; b = −23,5; с = 274; d = −23,475.
1.7 Вычислить число u. Определить предельную абсолютную погрешность числа u. Округлить число u и найти погрешность результата:
а) u = 2,51 – 2,486 + 1,5; б) u = –2,15 + 1,2 – 0,246; в) u = 0,356 – 2,4 + 2,11; г) u = 10,25 + 0,325 – 10,72.
1.8 Вычислить число u. Определить предельную относительную погрешность числа и. Округлить число u и найти погрешность результата:
а)  ; б)
; б) 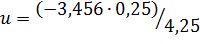 ;
;
в)  ; г)
; г) 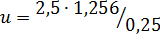 .
.
1.9 Вычислить, найти погрешность результата, округлить его и найти погрешность округления:
а)  , если
, если 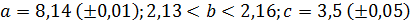 ; б)
; б)  , если
, если  ;
;
в)  , если
, если  ;
;
г) 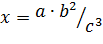 , если
, если 
 ;
;
д)  , если
, если 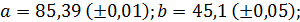
 .
.
Глава 2. Численные методы решения нелинейных уравнений.
Рассмотрим уравнение вида
f(x)= 0, (1)
где f(x) – функция действительной переменой.
В большинстве случаев формул для точного решения уравнения вида (1) не существует. Например, если f(x) – многочлен степени выше 4, то по теореме Абеля корни этого многочлена не могут быть выражены в радикалах через его коэффициенты. Ненулевые корни уравнения  также не выражаются с помощью элементарных функций. Поэтому на практике часто прибегают к приближенным методам решения уравнений, суть которых состоит в построении числовой последовательности
также не выражаются с помощью элементарных функций. Поэтому на практике часто прибегают к приближенным методам решения уравнений, суть которых состоит в построении числовой последовательности  , сходящейся к искомому корню х* уравнения (1).
, сходящейся к искомому корню х* уравнения (1).
Процесс нахождения корней уравнения (1) с помощью приближенных методов распадается на два этапа:
1. отделение действительных корней уравнения, т. е. нахождение отрезков, на которых содержится ровно один корень;
2. вычисление корня уравнения с заданной точностью.
Рассмотрим каждый из этапов подробнее.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 1741; Нарушение авторских прав?; Мы поможем в написании вашей работы!