Решение. Погрешности результатов арифметических операций

Решение.

Погрешности результатов арифметических операций.

Оценим погрешности результатов арифметических операций.

Утверждение 1. Предельная абсолютная погрешность суммы нескольких приближенных чисел, записанных в десятичной форме верными цифрами, равна сумме предельных абсолютных погрешностей слагаемых.

Замечание. При сложении приближенных чисел в полученном результате необходимо по правилам округления отбрасывать цифры тех разрядов справа, которых нет хотя бы в одном из слагаемых.

Утверждение 2. Предельная абсолютная погрешность разности двух приближенных чисел, записанных в десятичной форме верными цифрами, равна сумме предельных абсолютных погрешностей уменьшаемого и вычитаемого.

Замечание. При вычитании приближенных чисел в полученном результате необходимо по правилам округления отбрасывать цифры тех разрядов справа, которых нет хотя бы в одном из слагаемых.

Пример 1. Определить предельную абсолютную погрешность числа u = 7,3 + 3,62 – 9,678 = 1,242. Округлить число u и найти погрешность результата.

Найдем предельные абсолютные погрешности чисел 7,3, 3,62 и 9,678:

Δ_7,3 = 0,5∙10^-1=0,05; Δ_3,62 = 0,5∙10^-2=0,005; Δ_9,678 = 0,5∙10^-3=0,0005.

Тогда в силу утверждений 1 и 2 получим

Δ_u = Δ_7,3 + Δ_3,62 + Δ_9,678 = 0,05 + 0,005 + 0,0005 = 0,0555.

Так как в числе 7,3 наименьший разряд – десятые, то округляем число u до приближенного значения а = 1,2, следовательно, абсолютная погрешность округления Δ_а = | u – a | = |1,242 – 1,2| = 0,042.

Цифра 2 в записи приближенного значения а является верной, так как Δ_а = 0,042< 0,5∙10^-1 = 0,05.

Учитывая погрешность округления, для оценки погрешности результата Δ получим Δ = Δ_u + Δ_а = 0,0555 + 0,042 = 0,0975. Следовательно, можно записать, что u = 1,2 (± 0,0975).

Ответ. Δ_u = 0,0555; Δ = 0,0975; u ≈ 1,2 (± 0,0975).

Пример 2. Определить предельную абсолютную погрешность числа А = 2,25 – 2,7 + 0,26 = −0,19. Округлить число А и найти погрешность результата.

Найдем предельные абсолютные погрешности чисел 2,25, 2,7 и 0,26:

Δ_2,25 = 0,5∙10^-2=0,005; Δ_2,7 = 0,5∙10^-1=0,05; Δ_0,26 = 0,5∙10^-2=0,005.

Тогда в силу утверждений 1 и 2 получим

Δ _А = Δ_2,25 + Δ_2,7 + Δ_0,26 = 0,005 + 0,05 + 0,005 = 0,06.

Так как в числе 2,7 наименьший разряд – десятые, то округляем число А до приближенного значения а = −0,2, следовательно, абсолютная погрешность округления Δ_а = | А – a | = |−0,19 – (−0,2)| = 0,01.

Цифра 2 в записи приближенного значения а является верной, так как Δ_а = 0,01< 0,5∙10^-1 = 0,05.

Учитывая погрешность округления, для оценки погрешности результата Δ получим Δ = Δ _А + Δ_а = 0,06 + 0,01 = 0,07. Следовательно, можно записать, что u = −0,2 (± 0,07).

Ответ. Δ_u = 0,06; Δ = 0,07; u ≈ 1,2 (± 0,07).

Утверждение 3. Предельная относительная погрешность произведения нескольких приближенных чисел, записанных в десятичной форме верными цифрами, равна сумме предельных относительных погрешностей сомножителей.

Замечание. При умножении приближенных чисел в полученном результате необходимо сохранять столько значащих цифр, сколько имеет сомножитель с наименьшим количеством значащих цифр.

Утверждение 4. Предельная относительная погрешность частного от деления двух приближенных чисел, записанных в десятичной форме верными цифрами, равна сумме предельных относительных погрешностей делимого и делителя.

Замечание. При делении приближенных чисел в полученном результате необходимо сохранять столько значащих цифр, сколько их имеет приближенное данное с наименьшим количеством значащих цифр.

Пример 3. Определить предельную относительную погрешность числа 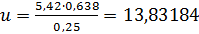. Округлить число u и найти погрешность результата.

Решение.

Найдем предельные относительные погрешности чисел 5,42, 0,638 и 0,25. Для этого сначала определим предельные абсолютные погрешности этих чисел:

Δ_5,42 = 0,5∙10^-2=0,005; Δ_0,638 = 0,5∙10^-3=0,0005; Δ_0,25 = 0,5∙10^-2=0,005.

Поэтому, в силу формулы (5) предельные относительные погрешности данных чисел будут равны:

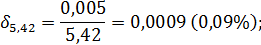
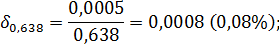
Тогда в силу утверждений 3 и 4 получим

δ_u = 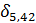+ + 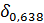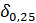= 0,0009 + 0,0008 + 0,02 = 0,0217 (2,17%).

Так как в числе 0,25 две значащие цифры, то округляем число u до приближенного значения а = 14, следовательно, абсолютная погрешность округления Δ_а = | u – a | = |13,83184 – 14| 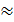0,1682.

Цифра 4 в записи приближенного значения а является верной, так как Δ_а = 0,1682 < 0,5∙10⁰ = 0,5.

Учитывая погрешность округления и то, что Δ _u = δ_u | u | = 0,0217∙13,83184 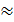0,3002, для оценки погрешности результата Δ получим Δ = Δ_u + Δ_а = 0,3002 + 0,1682 = 0,4684. Следовательно, можно записать, что u = 14 (± 0,4684).

Ответ. δ_u = 0,0217 (2,17%); Δ = 0,4684; u ≈ 14 (± 0,4684).

Пример 4. Определить предельную относительную погрешность числа 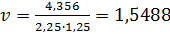. Округлить число 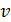и найти погрешность результата.

Решение.

Найдем предельные относительные погрешности чисел 4,356, 2,25 и 1,25. Для этого сначала определим предельные абсолютные погрешности этих чисел:

Δ_4,356 = 0,5∙10^-3=0,0005; Δ_2,25 = 0,5∙10^-2=0,005; Δ_1,25 = 0,5∙10^-2=0,005.

Поэтому, в силу формулы (5) предельные относительные погрешности данных чисел будут равны:

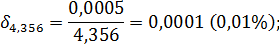
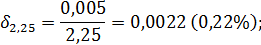
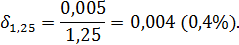
Тогда в силу утверждений 3 и 4 получим

δ_u = 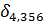+ + 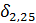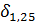= 0,0001 + 0,0022 + 0,004 = 0,0063 (0,63%).

Так как в числах 2,25 и 1,25 три значащие цифры, то округляем число 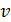до приближенного значения а = 1,55, следовательно, абсолютная погрешность округления Δ_а = | u – a | = |1,5488 – 1,55| 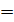0,0012.

Цифра 5 в записи приближенного значения а является верной, так как Δ_а = 0,0012 < 0,5∙10^-2 = 0,005.

Учитывая погрешность округления и то, что Δ _u = δ_u | u | = 0,0063∙1,5488 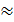0,0098, для оценки погрешности результата Δ получим Δ = Δ_u + Δ_а = 0,0098 + 0,0012 = 0,011. Следовательно, можно записать, что u = 1,55 (± 0,011).

Ответ. δ_u = 0,0063 (0,63%); Δ = 0,011; u ≈ 1,55 (± 0,011).

Утверждение 5. Предельная относительная погрешность степени приближенного числа, записанного в десятичной форме верными цифрами, равна произведению показателя степени на предельную относительную погрешность основания.

Замечание. 1) при возведении приближенного числа в степень с целым показателем в полученном результате необходимо сохранять столько значащих цифр, сколько имеет основание. 2) при извлечении корня из приближенного числа в результате нужно сохранить столько значащих цифр, сколько их имеет подкоренное число.

Пример 5. Вычислить объем куба со стороной а = 1,27 м.

Решение. V = а ³ = (1,27)³ = 2,0484 (м³).

Δ_а = 0,005; .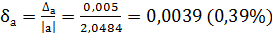

.

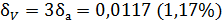Но δ_V = 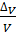, откуда Δ _V = δ_V ∙ V = 0,0117∙2,0484 = 0,024.

Если мы хотим округлить число V до приближенного значения V' = 2,05, то абсолютная погрешность округления

Δ _V = | V – V' | = |2,0484 – 2,05| = 0,0016.

Цифра 5 в записи приближенного значения является верной, так как

Δ _V < 0,5·10^-2 = 0,005.

Учитывая погрешность округления, можно записать, что

V = 2,05 (± 0,0256).

Ответ. V ≈ 2,05 (± 0,0256).

Дата добавления: 2014-12-27