
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод половинного деления (метод вилки)
Методы численного решения уравнений.
Упражнения.
2.1 Отделить корни уравнения и уточнить промежутки их изоляции:
а)  ; б)
; б) 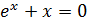 ; в)
; в) 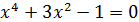 ; г)
; г) 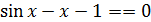 ; д)
; д) 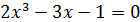 ; е)
; е) 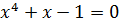 .
.
Перед тем, как рассмотреть некоторые из приближенных методов решения уравнений опишем приемы контроля точности нахождения приближенного значения корня:
Утверждение1. Если х* – точный, а х’ – приближенный корни уравнения f(x)= 0, принадлежащие отрезку [ a; b ], то справедлива оценка: 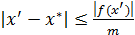 , где
, где 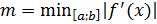 .
.
Утверждение 2. Если 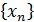 – последовательность приближенных значений корня х* уравнения
– последовательность приближенных значений корня х* уравнения 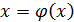 и функция
и функция 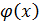 - непрерывно-дифференцируема на отрезке [ a; b ], причем на этом промежутке
- непрерывно-дифференцируема на отрезке [ a; b ], причем на этом промежутке 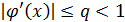 , то выполняется неравенство
, то выполняется неравенство
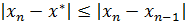 .
.
Метод вилки приближенного решения уравнения
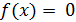 (1)
(1)
с точностью до ε, основан на доказательстве теоремы 2 (см. п. 2.1.), которое подробно разбирается в курсе математического анализа. Поэтому на самом доказательстве мы не будем останавливаться, но рассмотрим алгоритм метода, который напрямую следует из доказательства теоремы.
Замечание. Для оценки точности нахождения приближенного значения корня уравнения (1) будем использовать критерий, следующий из доказательства теоремы 2 (см. п. 2.1.): если 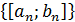 – система вложенных отрезков[6], построенная для нахождения приближенного значения корня уравнения (1) с точностью до ε и при некотором натуральном n, выполняется
– система вложенных отрезков[6], построенная для нахождения приближенного значения корня уравнения (1) с точностью до ε и при некотором натуральном n, выполняется  , то процесс решения заканчивается и в качестве приближенного значения корня х* следует взять величину
, то процесс решения заканчивается и в качестве приближенного значения корня х* следует взять величину 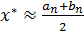 .
.
Алгоритм метода вилки. Пусть на отрезке [ a; b ] уравнение (1) имеет единственный корень х*. Значит на этом отрезке функция f(x) удовлетворяет условиям теоремы 2 (см. п. 2.2), т. е. f(x) непрерывна и монотонна на отрезке [ a; b ] и принимает на его концах значения разных знаков f(a)f(b)< 0.
1 шаг. Разделим отрезок [ a; b ] точкой 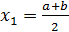 на два равных отрезка: [ a; х1 ] и [ х1; b ]. Если f(x1) = 0, то число х1 – точное решение уравнения (1), т. е. х* = х1. В противном случае, т. е., если f(x1)≠ 0, то либо f(a)f(х1)< 0, либо f(х1)f(b)< 0.
на два равных отрезка: [ a; х1 ] и [ х1; b ]. Если f(x1) = 0, то число х1 – точное решение уравнения (1), т. е. х* = х1. В противном случае, т. е., если f(x1)≠ 0, то либо f(a)f(х1)< 0, либо f(х1)f(b)< 0.
Если f(a)f(х1)< 0, то точное значения корня х* содержится в отрезке [ a; х1 ]. Если же f(х1)f(b)< 0, то точное значения корня х* содержится в отрезке [ х1; b ]. Для определенности предположим, что точное значения корня х* содержится в отрезке [ a; х1 ].
Рассмотрим абсолютное значение разности 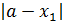 . Если
. Если 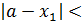
 , то процесс нахождения приближенного значения корня следует закончить и в качестве приближенного значения корня х* взять величину
, то процесс нахождения приближенного значения корня следует закончить и в качестве приближенного значения корня х* взять величину 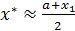 . Если же
. Если же 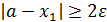 , то процесс решения продолжаем.
, то процесс решения продолжаем.
2 шаг. Так как f(a)f(х1)< 0, то берем отрезок [ a; х1 ] и разделим его точкой 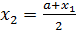 на два равных отрезка: [ a; х2 ] и [ х2; х1 ]. Если f(x2) = 0, то число х2 – точное решение уравнения (1), т. е. х* = х2. В противном случае, т. е., если f(x2)≠ 0, то либо f(a)f(х2)< 0, либо f(х2)f(х1)< 0.
на два равных отрезка: [ a; х2 ] и [ х2; х1 ]. Если f(x2) = 0, то число х2 – точное решение уравнения (1), т. е. х* = х2. В противном случае, т. е., если f(x2)≠ 0, то либо f(a)f(х2)< 0, либо f(х2)f(х1)< 0.
Если f(a)f(х2)< 0, то точное значения корня х* содержится в отрезке [ a; х2 ]. Если же f(х2)f(х1)< 0, то точное значения корня х* содержится в отрезке [ х2; х1 ]. Для определенности предположим, что точное значения корня х* содержится в отрезке [ х2; х1 ].
Рассмотрим абсолютное значение разности 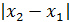 . Если
. Если  , то процесс нахождения приближенного значения корня следует закончить и в качестве приближенного значения корня х* взять величину
, то процесс нахождения приближенного значения корня следует закончить и в качестве приближенного значения корня х* взять величину 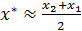 . Если же
. Если же 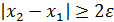 , то процесс решения продолжаем.
, то процесс решения продолжаем.
Т. е. на третьем шаге берем отрезок [ х2; х1 ], так как f(х2)f(х1)< 0, и делим его точкой 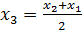 и т. д. Продолжая процесс пока не будет достигнута заданная точность ε.
и т. д. Продолжая процесс пока не будет достигнута заданная точность ε.
Пример 1. Методом вилки найти приближенные значения действительных корней уравнения 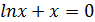 с точностью до ε= 0,01.
с точностью до ε= 0,01.
Решение.
1 этап. Уравнение 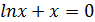 имеет единственный действительный корень х*, который расположен на отрезке [0,5; 1] (см. пример п. 2.1.).
имеет единственный действительный корень х*, который расположен на отрезке [0,5; 1] (см. пример п. 2.1.).
2 этап. Найдем значения функции  на концах отрезка [0,5; 1]:
на концах отрезка [0,5; 1]:
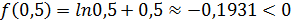 и
и 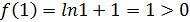 .
.
1 шаг. Разделим отрезок [0,5; 1] точкой 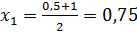 на два равных отрезка: [0,5; 0,75]и [0,75; 1]. Найдем значение функции f(x) в точке х 1= 0,75:
на два равных отрезка: [0,5; 0,75]и [0,75; 1]. Найдем значение функции f(x) в точке х 1= 0,75:
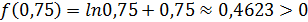 .
.
Так как f( 0,5 )f( 0,75 )< 0, то по теореме 2 (см. п. 2.1.), корень исходного уравнения расположен на отрезке[0,5; 0,75].
Так как 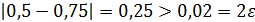 , то вычисления продолжаем.
, то вычисления продолжаем.
2 шаг. Разделим отрезок [0,5; 0,75] точкой 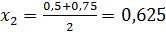 на два равных отрезка: [0,5; 0,625]и [0,625; 0,75]. Найдем значение функции f(x) в точке х2 = 0,625:
на два равных отрезка: [0,5; 0,625]и [0,625; 0,75]. Найдем значение функции f(x) в точке х2 = 0,625:
 .
.
Так как f( 0,5 )f( 0,625 )< 0, то по теореме 2 (см. п. 2.1.), корень исходного уравнения расположен на отрезке[0,5; 0,625].
Так как 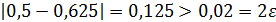 , то вычисления продолжаем.
, то вычисления продолжаем.
3 шаг. Разделим отрезок [0,5; 0,625] точкой 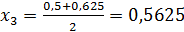 на два равных отрезка: [0,5; 0,5625]и [0,5625; 0,625]. Найдем значение функции f(x) в точке х3 = 0,5625:
на два равных отрезка: [0,5; 0,5625]и [0,5625; 0,625]. Найдем значение функции f(x) в точке х3 = 0,5625:
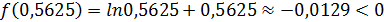 .
.
Так как f( 0,5625 )f( 0,625 )< 0, то по теореме 2 (см. п. 2.1.), корень исходного уравнения расположен на отрезке[0,5625; 0,625].
Так как 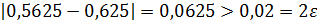 , то вычисления продолжаем.
, то вычисления продолжаем.
4 шаг. Разделим отрезок [0,5625; 0,625] точкой 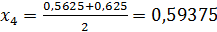 на два равных отрезка: [0,5625; 0,59375]и [0,59375; 0,625]. Найдем значение функции f(x) в точке х4 = 0,59375:
на два равных отрезка: [0,5625; 0,59375]и [0,59375; 0,625]. Найдем значение функции f(x) в точке х4 = 0,59375:
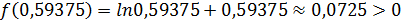 .
.
Так как f( 0,5625 )f( 0,59375 )< 0, то по теореме 2 (см. п. 2.1.), корень исходного уравнения расположен на отрезке[0,5625; 0,59375].
Так как 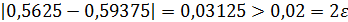 , то вычисления продолжаем.
, то вычисления продолжаем.
5 шаг. Разделим отрезок [0,5625; 0,59375] точкой 
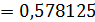 на два равных отрезка: [0,5625; 0,578125]и [0,578125; 0,59375]. Найдем значение функции f(x) в точке х5 = 0,578125:
на два равных отрезка: [0,5625; 0,578125]и [0,578125; 0,59375]. Найдем значение функции f(x) в точке х5 = 0,578125:
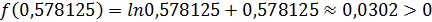 .
.
Так как f( 0,5625 )f( 0,578125 )< 0, то по теореме 2 (см. п. 2.1.), корень исходного уравнения расположен на отрезке[0,5625; 0,578125].
Так как  , то можно сделать вывод о том, что необходимая точность достигнута и в качестве приближенного значения корня х* уравнения
, то можно сделать вывод о том, что необходимая точность достигнута и в качестве приближенного значения корня х* уравнения 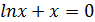 возьмем величину
возьмем величину 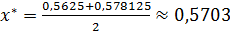 .
.
График функции 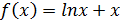 , иллюстрирующий разобранный пример, приведен на рисунке 2.
, иллюстрирующий разобранный пример, приведен на рисунке 2.
| Рисунок 2 |
Ответ.
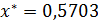 с точностью до ε= 0,01.
с точностью до ε= 0,01.
Пример 2. Методом вилки найти приближенное значение положительного действительного корня уравнения 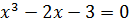 с точностью до ε= 0,01.
с точностью до ε= 0,01.
Решение.
1 этап. Отделим корни уравнения 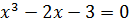 . Для этого рассмотрим функцию
. Для этого рассмотрим функцию 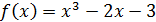 . Она определена и непрерывна для любого
. Она определена и непрерывна для любого 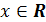 . Так как
. Так как 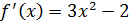 и
и 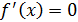
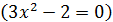 при
при 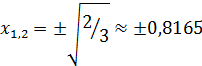 , а
, а 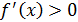 при
при 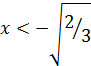 или
или 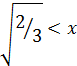 и
и 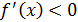 при
при 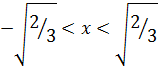 , то функция
, то функция 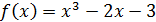 строго возрастает на интервалах
строго возрастает на интервалах 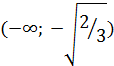 и
и 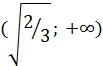 и убывает на интервале
и убывает на интервале 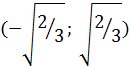 . Следовательно, на этих интервалах уравнение
. Следовательно, на этих интервалах уравнение 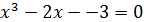 может иметь корни.
может иметь корни.
В условиях задачи сказано найти приближенное значение положительного корня, поэтому рассмотрим интервалы 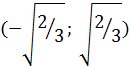 , а точнее
, а точнее 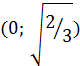 , и
, и 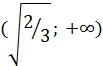 . Так как
. Так как 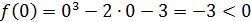 и
и 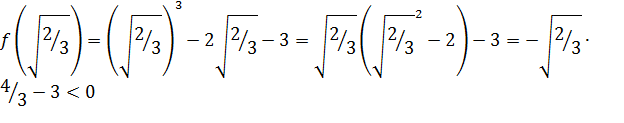 , то на интервале
, то на интервале 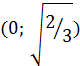 исходное уравнение корней не имеет. Поэтому остается интервал
исходное уравнение корней не имеет. Поэтому остается интервал 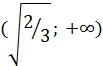 . Так как на этом интервале
. Так как на этом интервале 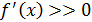 , то на нем уравнение
, то на нем уравнение 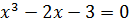 имеет единственный корень.
имеет единственный корень.
Что бы уточнить промежуток существования корня запишем уравнение в эквивалентной форме: 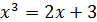 и
и
| Рисунок 3 |
построим на
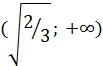 графики функций
графики функций 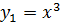 и
и 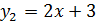 . Абсцисса точи пересечения графиков этих функций и будет точным значением корня х* уравнения
. Абсцисса точи пересечения графиков этих функций и будет точным значением корня х* уравнения 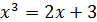 , а, следовательно, в силу эквивалентности, и исходного уравнения.
, а, следовательно, в силу эквивалентности, и исходного уравнения.
| х * |
2 этап. Найдем значения функции 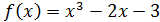 на концах отрезка [1,8; 2]:
на концах отрезка [1,8; 2]:
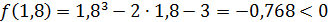 и
и 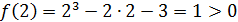 .
.
1 шаг. Разделим отрезок [1,8; 2] точкой 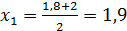 на два равных отрезка: [1,8; 1,9]и [1,9; 2]. Найдем значение функции f(x) в точке х 1= 1,9:
на два равных отрезка: [1,8; 1,9]и [1,9; 2]. Найдем значение функции f(x) в точке х 1= 1,9:
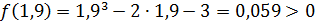 .
.
Так как f( 1,8 )f( 1,9 )< 0, то по теореме 2 (см. п. 2.1.), корень исходного уравнения расположен на отрезке[1,8; 1,9].
Так как 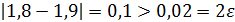 , то вычисления продолжаем.
, то вычисления продолжаем.
2 шаг. Разделим отрезок [1,8; 1,9] точкой 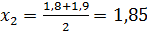 на два равных отрезка: [1,8; 1,85]и [1,85; 1,9]. Найдем значение функции f(x) в точке х2 = =1,85:
на два равных отрезка: [1,8; 1,85]и [1,85; 1,9]. Найдем значение функции f(x) в точке х2 = =1,85:
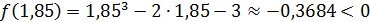 .
.
Так как f( 1,85 )f( 1,9 )< 0, то по теореме 2 (см. п. 2.1.), корень исходного уравнения расположен на отрезке[1,85; 1,9].
Так как 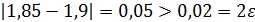 , то вычисления продолжаем.
, то вычисления продолжаем.
3 шаг. Разделим отрезок [1,85; 1,9] точкой  на два равных отрезка: [1,85; 1,875]и [1,875; 1,9]. Найдем значение функции f(x) в точке х3 = 1,875:
на два равных отрезка: [1,85; 1,875]и [1,875; 1,9]. Найдем значение функции f(x) в точке х3 = 1,875:
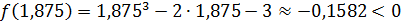 .
.
Так как f( 1,875 )f( 1,9 )< 0, то по теореме 2 (см. п. 2.1.), корень исходного уравнения расположен на отрезке[1,875; 1,9].
Так как 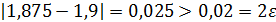 , то вычисления продолжаем.
, то вычисления продолжаем.
4 шаг. Разделим отрезок [1,875; 1,9] точкой 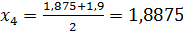 на два равных отрезка: [1,875; 1,8875]и [1,8875; 1,9]. Найдем значение функции f(x) в точке х4 = 1,8875:
на два равных отрезка: [1,875; 1,8875]и [1,8875; 1,9]. Найдем значение функции f(x) в точке х4 = 1,8875:
 .
.
Так как f( 1,8875 )f( 1,9 )< 0, то по теореме 2 (см. п. 2.1.), корень исходного уравнения расположен на отрезке[1,8875; 1,9].
Так как 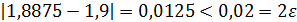 , то можно сделать вывод о том, что необходимая точность достигнута и в качестве приближенного значения корня х* уравнения
, то можно сделать вывод о том, что необходимая точность достигнута и в качестве приближенного значения корня х* уравнения 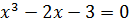 возьмем величину
возьмем величину 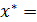
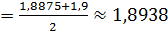 .
.
Ответ. 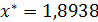 с точностью до ε= 0,01.
с точностью до ε= 0,01.
|
|
Дата добавления: 2014-12-27; Просмотров: 5449; Нарушение авторских прав?; Мы поможем в написании вашей работы!