Решение. 1 этап. Отделим корни уравнения

1 этап. Отделим корни уравнения 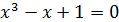. (8)

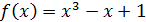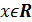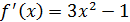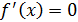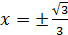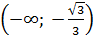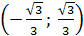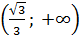Рассмотрим функцию . Она определена и непрерывна для любого . А так как и при , то функция строго монотонна на интервалах , и . Следовательно, на каждом из этих интервалов уравнение 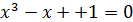может иметь корень, причем единственный.

Что бы уточнить наличие корня запишем уравнение (8) в эквивалентной форме:

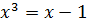(9)

х ^*

и построим графики функций

Рисунок 15

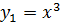и 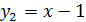(рис. 15). Абсцисса точки пересечения графиков этих функций и будет точным значением корня х^* уравнения (9), а, следовательно, в силу эквивалентности, и уравнения (8).

Из рисунка видно, что точное значение корня х^* уравнения (8) лежит на отрезке .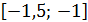

2 этап. Представим уравнение 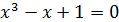в ви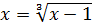де , где 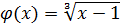, и проверим выполнение двух условий теоремы, определяющей применимость метода итераций:

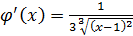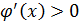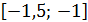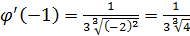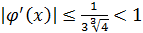а) . Нетрудно заметить, что на отрезке и ее значения возрастают на нем. Так как ,то на 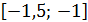, первое условие выполнено;

б) Выполнение второго условия теоремы, т.е. условия на отрезке 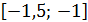, в нашем случае должно сводиться к выполнению неравенств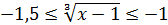а на 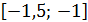. Его решение эквивалентно решению системы двух неравенств

.

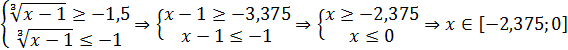Таким образом, неравенство 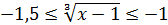справедливо на промежутке 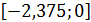и, следовательно, справедливо на промежутке 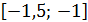, который содержится в 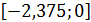. Значит второе условие теоремы также выполнено.

3) В качестве начального приближения возьмем значение х ₁ = −1,25, которое является серединой промежутка .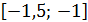

Найдем последующие приближения, используя рекуррентное соотношение x_i = φ (х_{i -1}) или в данном случае x_i = 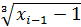, где i = 2, 3, ….

x ₂ = .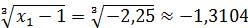

Оценим разность 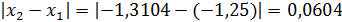. Так как 0,0604 > 0,01, то процесс итерации продолжаем.

x ₃ = .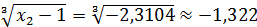

Оценим разность 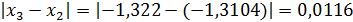. Так как 0,0116 > 0,01, то процесс итерации продолжаем.

x ₄ = .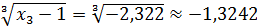

Оценим разность 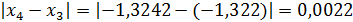. Так как 0,0022 < 0,01, то процесс итерации закончен.

Следовательно, приближенное значение действительного корня уравнения 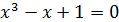с точностью ε = 0,01 равно .

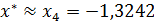Ответ. 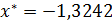с точностью до ε = 0,01.

Пример 2. Методом итерации найти приближенное значение положительного действительного корня уравнения 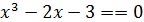с точностью до ε= 0,01.

Решение.

1 этап. Отделим корни уравнения 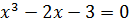. В примере 2 п. 2.2.1. было показано, что точное значение положительного корня х^* данного уравнения лежит на отрезке [1,8; 2].

2 этап. Представим уравнение 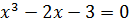в ви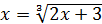де , где 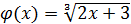, и проверим выполнение двух условий теоремы, определяющей применимость метода итераций:

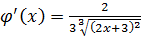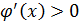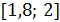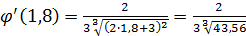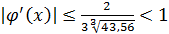а) . Нетрудно заметить, что на отрезке и ее значения убывают на нем. Так как ,то на 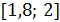, первое условие выполнено;

б) Выполнение второго условия теоремы, т.е. условия на отрезке 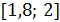, в нашем случае должно сводиться к выполнению неравенства на 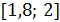. Его решение эквивалентно решению системы двух неравенств

.

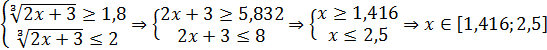Таким образом, неравенство справедливо на промежутке 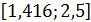и, следовательно, справедливо на промежутке 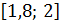, который содержится в 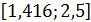. Значит второе условие теоремы также выполнено.

3) В качестве начального приближения возьмем значение х ₁ = 1,9, которое является серединой промежутка .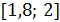

Найдем последующие приближения, используя рекуррентное соотношение x_i = φ (х_{i -1}) или в данном случае x_i = 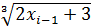, где i = 2, 3, ….

x ₂ = .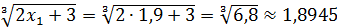

Оценим разность 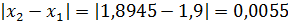. Так как 0,0055 < 0,01, то процесс итерации закончен.

Следовательно, приближенное значение действительного корня уравнения 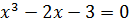с точностью ε = 0,01 равно .

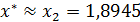Ответ. 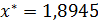с точностью до ε = 0,01.

Методом итераций можно вычислять приближенные значения иррациональных чисел.

Покажем, как это делается. Пусть требуется вычислить приближенное значение 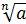, где а – некоторое положительное действительное число. Эта задача равносильна отысканию положительного действительного корня алгебраического уравнения .

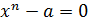Преобразуем это уравнение к виду х = φ (х). Для этого к обеим частям прибавим слагаемое nxⁿ. В результате получим 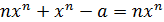или 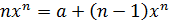. Разделим обе части на nx^{n -1}, получим

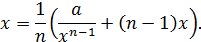
Таким образом

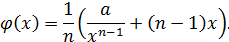
Условия теоремы применимости метода итерации будут выполняться вблизи искомого корня.

Если за начальное приближение х ₁, взять грубое приближенное значение искомого корня, то последующие приближения х ₂, х ₃,... вычисляют по формуле

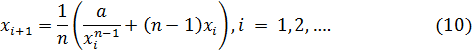
Процесс следует закончить после выполнения неравенства 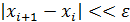, где ε – выбранная нами точность приближения.

Пример 3. Вычислить приближенное значение 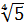с точностью до ε= 0,01.

Дата добавления: 2014-12-27