Сложение (вычитание) матриц

Операции над матрицами.

Равенство матриц.

Матрицы одного размера А = (a_ij) и В = (b_ij) называ­ются равными, если равны их соответствующие элементы, т.е. a_ij = b_ij.

Так, матрица А = равна матрице В = (А = В), но матрица А не равна матрице С = , т.к. 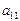с ₁₁ (порядок расположения элементов матрицы важен для проверки равенства матриц).

4.1.Транспонирование матриц

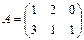Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется транспонированной к данной и обозначается А ^т.

Пример 1.1. Транспонируйте матрицу

Решение. Операция транспонирования матрицы А осуществляется следующим образом: первая строка матрицы А становится первым столбцом матрицы А ^Т, вторая строка А - вторым столбцом А ^т, т.е.

А ^т =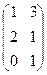

Складывать (вычитать) можно только такие матрицы, которые имеют одинаковую размерность.

Суммой (разностью) матриц А = (a_ij) и В = (b_ij) называется матрица С, элементы которой равны суммам (разно­стям) соответствующих элементов матриц А и В, т.е. c_ij = a_ij + b_ij (c_ij = a_ij - b_ij).

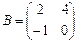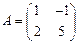Пример 1.2. Найдите сумму и разность матриц и

Решение:

D = A – B =

Операция сложения матриц обладает следующими свойствами:

1. A + B = B + A;

2. (A + B) + C = A + (B + C).

Дата добавления: 2014-12-27