Общие свойства одномерного движения

151. Частица движется в некотором потенциале U (x).Какое из

перечисленных уравнений является стационарным уравнением Шредингера для этой частицы?

	∂Ψ( x, t )					d
А. i	^=	−					+ U (x)	Ψ(x, t)
∂ t	2 m dx

Б. −

_В. ∂|

Г. − i

		d
				+ U (x)	f n (x)= En f n (x)
2 m dx
Ψ(x, t ) |^2	+ divJ (x, t) = 0
∂ t

_dx^d f _p (x)= pf _p (x)

152. Частица движется в некотором одномерном потенциале U (x).Оператор Гамильтона для этой частицы – это

А. −

d ^2

+ U (x)

Б. −

d ^2

− U (x)

2 m dx ^2

2 m dx ^2

В. оператор умножения на функцию U (x)

Г. −

d ^2

2 m

dx ^2

153.

Что

значит решить стационарное

уравнение

Шредингера

d

−

+ U (x)

f n (x)= En f n (x)?

2 m dx

А. найти все решения f _n (x)

Б. найти все конечные решения f _n (x)

В. найти все энергии E_n, при которых это уравнение имеет реше-ния, и сами решения

Г. найти все энергии E_n, при которых это уравнение имеет конеч-ные решения f _n (x), и сами эти решения

154. Какое состояние называется основным?

А. собственное состояние гамильтониана, отвечающее непрерыв-ному спектру, и имеющее минимальную энергию Б. собственное состояние гамильтониана, отвечающее дискретному спектру и имеющее минимальную энергию

В. собственное состояние гамильтониана, отвечающее непрерыв-ному спектру и имеющее максимальную энергию Г. собственное состояние гамильтониана, отвечающее дискретному спектру и имеющее максимальную энергию

155. Какое состояние называется первым возбужденным?

А. собственное состояние гамильтониана, отвечающее дискретно-му спектру и имеющее минимальную энергию Б. собственное состояние гамильтониана, отвечающее дискретному

спектру и имеющее вторую по счету (в порядке возрастания) энер-гию В. собственное состояние гамильтониана, отвечающее дискретному

спектру и имеющее третью по счету (в порядке возрастания) энер-гию Г. собственное состояние гамильтониана, отвечающее непрерыв-

ному спектру и имеющее вторую по счету (в порядке возрастания) энергию 156. Какие состояния называются связанными?

А. собственные состояния гамильтониана, волновые функции ко-торых затухают при x → ±∞

Б. собственные состояния оператора импульса, волновые функции которых затухают при x → ±∞

В. собственные состояния гамильтониана, волновые функции кото-рых не обращаются в бесконечность при конечных значениях ко-ординат Г. собственные состояния гамильтониана, волновые функции кото-

рых не затухают при x → ±∞

157. Какие состояния являются связанными в одномерной задаче?А. двукратно вырожденные состояния дискретного спектра Б. невырожденные стационарные состояния непрерывного спектра В. двукратно вырожденные состояния непрерывного спектра

Г. невырожденные стационарные состояния дискретного спектра

Б. U ₀ < E < U ₁

158.Потенциальная энергия стремится к	U (x)
+∞ при x → ±∞ («потенциальная яма»,
см. рисунок). Все уровни энергии частицы
в такой яме	x
А. не вырождены

Б. двукратно вырождены В. часть уровней не вырождена, часть двукратно вырождена

Г. вырождение уровней зависит от конкретного вида потенциала 159. Частица движется в некотором потен-

циале U (x).	Известно,	что	U (x)→ +∞	U (x)
при x → ±∞ (см. рисунок).	Существуют
ли среди стационарных состояний частицы			x
состояния, относящиеся к непрерывному
спектру?
А. да
Б. нет
В. в некоторых случаях да, в некоторых случаях нет
Г. это зависит от потенциала
160.Дан график зависимости потен-	U (x)
циальной энергии U (x)	от координа-
U 2
ты x (см. рисунок). Указать области,
в которых могут существовать ста-	U 1		x
ционарные состояния	дискретного	a 1
спектра				U 0
А. E < U 0	Б. U 0 < E < U 1
В. a 1 < x < a 2	Г. x < a 1 и x > a 2
161.Дан график зависимости потенциальной энергии U (x)	от ко-

ординаты x (см. рисунок к задаче 160). Указать области, в которых могут существовать стационарные состояния непрерывного спек-

тра

А. E > U ₁ В. a ₁ < x < a ₂

Г. x < a ₁ и x > a ₂

162. Дан график зависимости потенциальной энергии U (x)от ко-ординаты x (см. рисунок к задаче 160). При каких энергиях суще-

ствуют невырожденные стационарные состояния непрерывного спектра?

А. при E > U 2	Б. при U 1 < E < U 2
В. при U 0 < E < U 1	Г. при E < U 0

163. Дан график зависимости потенциальной энергии от координа-ты x (см. рисунок к задаче 160). При каких энергиях заведомо не существует стационарных состояний?

А. E < U 0	Б. U 0 < E < U 1
В. E > U 2	Г. U 1 < E < U 2
164.Потенциальная энергия обращается в	U (x)
нуль при	x → ±∞(см.рисунок).Какова
кратность вырождения собственных зна-
чений гамильтониана, относящихся к не-	x
прерывному спектру?
А. не вырождены
Б. двукратно вырождены

В. часть собственных значений не вырождена, часть двукратно вы-рождена Г. кратность вырождения зависит от конкретного вида потенциала

165. Дан график зависимости потенциальной энергии U (x)от ко-

ординаты x (см. рисунок). При каких энергиях существуют стационарные состояния дискретного спектра?

А. при E > 0

Б. при E < 0

В. при E < U ₀

U (x)

U ₀

x

Г. состояний дискретного спектра в таком потенциале нет 166. Частица движется в некотором потен-

циале U (x). Известно, что U (x) → +∞ при	U (x)
x → +∞и U (x)→ −∞при x → −∞(см.	x
рисунок). Существуют ли среди стационар-
ных состояний частицы состояния, относя-
щиеся к дискретному спектру?
А. да	Б. в некоторых случаях да, в некоторых случаях нет
В. нет	Г. это зависит от конкретного вида потенциала

167. Частица движется в некотором потенциале U (x).Известно,что U (x) → +∞ при x → +∞ и U (x) → −∞ при x → −∞ (см. рисунок к задаче 166). Существуют ли среди стационарных состоя-

ний частицы двукратно вырожденные состояния?
А. да		Б. в некоторых случаях да, в некоторых случаях нет
В. нет		Г. зависит от потенциала
168.Частица движется в потенциале	U (x)
U (x),график которого представлен	U 2
на рисунке. Какой формулой описы-
вается	асимптотика	собственной	U 1			E
функции оператора Гамильтона при	a 1		a 2	x
энергии	E	(показана на рисунке)
U 0
при x → −∞?
А. exp(− kx), k =	2 mE / ^2
Б. exp(kx),	k =	2 m (U 2 − E) /
В. exp(kx),	k =	2 mE /
Г. exp(kx),	k =	2 m (E − U 2) /

169. Частица движется в потенциале U (x),график которого пред-ставлен на рисунке к задаче 168. Какой формулой описывается асимптотика собственной функции гамильтониана при энергии E

(показана на рисунке) при x →∞(k = 2 m (E − U ₁) / ²)?

А. exp(− kx) Б. exp(ikx),

В. линейная комбинация функций exp(ikx) Г. линейная комбинация функций exp(kx) 170. Частица движется в потенциале

U (x),график которого представленна рисунке. Пусть некоторая энергия E (показана на рисунке)являетсясобственным значением гамильто-ниана. Какими формулами описыва-ются асимптотики соответствующей

и exp(− ikx),

и exp(− kx),

U (x)

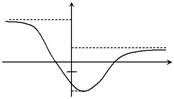^U 2

^U 1

1 E 2 x

^U 0

собственной функции при x → −∞ и x →∞?

А.

exp(k

x),

k

=

2 m (U

− E) /

,

и

exp(− k x),

k =2 m (U

− E) / ^2

Б.

exp(ik

x),

k

=

2 m (U

− E) /

,

и

exp(ik x),

k =2 m (U

− E) / ^2

В.

exp(− k

x),

k

=

2 m (U

− E) /

^2,

и

exp(k x),

k =2 m (U

− E) / ^2

Г. другими

171. Частица движется в потенциале U (x),который стремится к

некоторым постоянным при x → ±∞ (см. рисунок к задаче 170). Как ведут себя волновые функции двукратно вырожденных ста-ционарных состояний при x → ±∞?

А. растут Б. затухают

В. осциллируют Г. на одной бесконечности затухают, на другой осциллируют

172. Частица движется в потенциале U (x),который стремится к

некоторым постоянным при x → ±∞ (см. рисунок к задаче 170). Как ведут себя волновые функции невырожденных состояний не-прерывного спектра при x → ±∞?

А. растут Б. затухают

В. осциллируют Г. на одной бесконечности затухают, на другой осциллируют

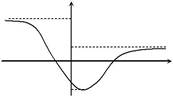
173. Что утверждает осцилляционная теорема?

А. что решения стационарного уравнения Шредингера, отвечаю-щие дискретному спектру, осциллируют Б. что решения стационарного уравнения Шредингера, отвечающие непрерывному спектру, осциллируют

В. что число нулей (узлов) n -го решения стационарного уравнения Шредингера, отвечающего дискретному спектру, равно n

Г. что число нулей (узлов) n -го решения стационарного уравнения Шредингера, отвечающего непрерывному спектру, равно n

174. Частица движется в некотором потенциале U (x),который

обращается в нуль при x → ±∞. Сколько узлов имеет волновая функция третьего возбужденного состояния дискретного (четвер-того по счету состояния в порядке возрастания энергии)?

А. 1	Б. 2	В. 3	Г. 4
175.На рисунке сплошной и пунктирной	f (x)
линией показаны графики двух собствен-
ных функций одномерного оператора Га-
мильтона. Какая из этих функций отвеча-	x
ет большему собственному значению?
А. сплошная		Б. пунктирная

В. эти функции отвечают вырожденным по энергии состояниям

Г. информации для ответа недостаточно
176.Собственная функция одномерного
оператора	Гамильтона	представлена	на	f (x)
рисунке. Что можно сказать о соответст-	x
вующем собственном значении?
А. относится к дискретному спектру
Б. относится к непрерывному спектру
В. двукратно вырождено
Г. информации для ответа недостаточно
177.Собственная функция одномерного	f (x)
оператора	Гамильтона	представлена	на
рисунке. Какому собственному состоянию
отвечает эта функция?			x
А. второму состоянию дискретного спек-
тра (в порядке возрастания энергии)
Б. третьему состоянию дискретного спектра
В. четвертому состоянию дискретного спектра
Г. пятому состоянию дискретного спектра
178.Собственная функция одномерного	f (x)
оператора	Гамильтона	затухает при
x → −∞и осциллирует при x →∞(см.
рисунок). Какое утверждение относи-	x
тельно свойств этой функции справед-

ливо?

А. эта функция отвечает дискретному спектру Б. эта функция отвечает невырожденному состоянию непрерывно-го спектра

В. эта функция отвечает двукратно вырожденному состоянию не-прерывного спектра Г. все перечисленное неверно

179. Потенциальная энергия частицы U (x)–четная функция ко-ординаты. Что можно сказать о коммутаторе операторов Гамиль-

ˆ ˆ	для такой частицы?
тона и четности H, P
А. равен нулю
Б. не равен нулю
В. зависит от конкретного вида потенциала
	ˆ	ˆ
Г. четность потенциала и коммутатор операторов H	и P никак не

связаны друг с другом

180. Частица движется в потенциале U (x).Коммутатор операто-

ров Гамильтона и четности ^ˆ для такой частицы равен

P

А. нулю Б. U (− x)

В. (U (x) − U (− x))

(− −) ^ˆ

Г. U (x) U (x) P

181. Потенциальная энергия частицы–четная функция координа-ты. Волновая функция третьего возбужденного стационарного со-стояния дискретного спектра (четвертого по счету состояния в по-рядке возрастания энергии)

А. четная	Б.	нечетная
В. неопределенной четности	Г.	четность зависит от кон-
кретного вида потенциала

182. Потенциальная энергия частицы U (x)= αx ⁴,где α >0–не-

которое число. Волновая функция четвертого возбужденного со-стояния дискретного спектра (пятого по счету состояния в порядке возрастания энергии)

А. четная Б. нечетная

В. неопределенной четности Г. четность зависит от α

183. Потенциальная энергия частицы U (x)–четная функция ко-

ординаты. Что можно сказать о волновых функциях стационарных состояний дискретного спектра?

А. все четные Б. все нечетные

В. не обладают определенной четностью Г. четность чередуется (четная-нечетная-четная и т.д.) с увеличе-нием энергии состояния

184. Потенциальная энергия частицы U (x)–нечетная функция

координаты. Что можно сказать о волновых функциях стационар-ных состояний дискретного спектра?

А. все четные Б. все нечетные

В. не обладают определенной четностью Г. четность чередуется (четная-нечетная-четная и т.д.) с увеличе-нием энергии состояния

185. Потенциальная энергия частицы U (x)–четная функция ко-

ординаты. Что можно сказать о волновых функциях стационарных состояний непрерывного спектра?

А. все четные Б. все нечетные

В. их можно выбрать так, чтобы одна была четная, вторая нечетная Г. четность чередуется (четная-нечетная-четная и т.д.) с увеличе-нием энергии состояния

186. Потенциальная энергия частицы U (x)–нечетная функция

координаты. Что можно сказать о волновых функциях стационар-ных состояний непрерывного спектра?

А. все четные Б. все нечетные

В. можно выбрать так, чтобы одна была четная, вторая нечетная Г. обладают неопределенной четностью

Дата добавления: 2014-12-24