Гармонический осциллятор

226. Какой формулой определяются энергии собственных состоя-ний одномерного гармонического осциллятора с частотой ω?

А.	ω (n ^2+1/ 2)	Б. ω (n +1/ 2)	В. ωn
Г.	ωn ^2(n =0,1,2,3,…)

227. Какой формулой определяются собственные функции гамиль-

тониана гармонического	осциллятора (x = x /	/ mω – безраз-
мерная координата осциллятора)?
А. Pn (x)exp (− x ^2 / 2)	(Pn	– полиномы Лежандра)
Б. Ln (x)exp (− x ^2 / 2)	(Ln	– полиномы Лагерра)

В. P_n ^m (x) exp (− x ² / 2) (P_n ^m – присоединенные полиномы Лежан-

дра)

Г. H _n (x) exp (− x ² / 2) (H_n – полиномы Эрмита, n = 0,1,2,3,…). 228. Какой формулой определяются собственные функции гамиль-

тониана гармонического осциллятора	(x = x /	/ mω –	безраз-
мерная координата осциллятора)?
А. H n (x) exp (− x ^2 / 2)	Б.	H n (x) exp(− x ^4/ 2)
В. H n (x) exp (− x / 2)	Г.	H n (x) exp(− x ^2)	(Hn -
полиномы Эрмита, n = 0,1,2,3,…).
229.Чему равен коэффициент перед x ^99	в сотом полиноме Эрмита
H 100(x)?
А. 1	Б. ½	В. 0	Г. –1

230.Чему равен коэффициент перед x ^2	в восемьдесят седьмом по-
линоме Эрмита H 87 (x)?
А. 1	Б. ½	В. 0	Г. –1

231. Какой формулой определяется условие ортогональности поли-номов Эрмита?

А.	^+∞∫ H n (x) H m (x) dx ∼ δnm	Б.	^+∞∫ H n (x) H m (x) x ^2 dx ∼ δnm
	−∞		−∞
В.	^+∞∫ H n (x) H m (x) e ^− ^x ^2 dx ∼ δnm	Г.	^+∞∫ H n (x) H m (x)sin x dx ∼ δnm
	−∞		−∞

232. Все уровни энергии одномерного гармонического осциллятораА. не вырождены Б. двукратно вырождены В. часть уровней не вырождена, часть - двукратно вырождена

Г. кратность вырождения n -го уровня энергии равна n

233. Какая величина,составленная из параметров гармоническогоосциллятора с массой m и частотой ω, имеет размерность длины (то есть является параметром длины для осциллятора)?

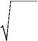
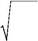
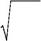
А.	m	Б.		В.	m	Г.	mω
ω	mω	ω

234. Какая величина,составленная из параметров гармоническогоосциллятора с массой m и частотой ω, имеет размерность энергии (то есть является параметром энергии для осциллятора)?

А. ω Б. / ω В. m ω Г. m / ω

235. Какая величина,составленная из параметров гармоническогоосциллятора с массой m и частотой ω, имеет размерность им-пульса (то есть является параметром импульса для осциллятора)?

А.		Б. mω	В. m ω	Г.
mω	mω

236. Волновая функция гармонического осциллятора в некоторыймомент времени имеет вид (1 + 2 x)exp(- x ² / 2) (x = x / / mω –

безразмерная координата осциллятора). Какие значения энергии осциллятора могут быть обнаружены при измерениях?

А. только	ω / 2и3 ω / 2	Б. только		ω / 2и5 ω / 2
В. только 3	ω / 2	Г. только		ω / 2

237. Волновая функция гармонического осциллятора в некоторыймомент времени является четной функцией координаты. Можно ли при измерениях энергии осциллятора в этом состоянии обнаружить

значение 3 ω / 2?

А. да Б. нет В. зависит от способа измерения

Г. зависит от волновой функции 238. Волновая функция гармонического осциллятора в некоторый

момент времени имеет неопределенную четность. Можно ли при измерениях энергии осциллятора в этом состоянии обнаружить

значение 3	ω / 4?
А. да	Б. это зависит от способа измерения
В. нет	Г. это зависит от волновой функции
239.	Осциллятор находится в n -м стационарном состоянии. Чему
равна средняя координата осциллятора в этом состоянии?
А.	/ mω	Б. n / mω	В.	n / mω	Г. 0
240.	При измерении энергии осциллятора были обнаружены два
значения	ω / 2с вероятностью¼и3	ω / 2с вероятностью¾.

Средняя энергия осциллятора в этом состоянии равна

А.	E	= 5 ω / 2	Б.	E	= 5 ω / 4	В.	E	= 5 ω / 3
Г.	E	= 5 ω / 6

241. При измерении энергии осциллятора в момент времени t =0были обнаружены два значения ω / 2 с вероятностью ¼ и 3 ω / 2 с вероятностью ¾. Чему равна средняя четность осциллятора в не-который момент времени t = t ₀?

А.			= −1/ 2	Б.		= − t 0 ω / 2
P	P
В.		= +1/ 2	Г.		= t 0 ω / 2
P	P

242. Осциллятор находится в таком состоянии,в котором его сред-

няя четность равна P = 3/ 4. Какие значения энергии осциллятора можно обнаружить при измерениях в этом состоянии?

А.	ω / 2и3 ω / 2	Б. 3 ω / 2 и 5 ω / 2
В. 5	ω / 2и7 ω / 2	Г. мало информации, чтобы ответить

243. Волновая функция гармонического осциллятора в некоторыймомент времени имеет вид (1 − 10 x ²) exp(− x ² / 2) (x = x / / mω

– безразмерная координата осциллятора). Какие значения энергии осциллятора могут быть обнаружены при измерениях?

А. только	ω / 2,3	ω / 2и5 ω / 2
Б. только 3	ω / 2и5 ω / 2
В. только 3 ω / 2
Г. только	ω / 2и5	ω / 2

244. Волновая функция гармонического осциллятора в некоторыймомент времени имеет вид (1 − 10 x ⁶)exp(− x ² / 2) (x = x / / mω

– безразмерная координата осциллятора). Какие значения энергии осциллятора могут быть обнаружены при измерениях?

А. только ω / 2 и 13 ω / 2 Б. только 13 ω / 2

В ω / 2, 5 ω / 2 и 13 ω / 2 Г. только ω / 2, 5 ω / 2, 9 ω / 2 и 13 ω / 2

245. Осциллятор находится в2007стационарном состоянии(ос-новное состояние – n = 0). Чему равна вероятность обнаружить осциллятор в бесконечно малом интервале dx вблизи точки x = 0?

А. dw =		dx	Б. dw =		dx	В. dw = 2007 dx
	2007^2

Г. 0

246. При измерениях энергии осциллятора обнаружены нулевое ивторое собственные значения с вероятностями w ₀ =1/ 4 и

w ₂=3/ 4.Чему равна средняя энергия осциллятора?

А. E = 2 ω Б. E = 3 ω В. E = 4 ω Г. E = 5 ω

247. Волновая функция осциллятора в момент времени t =0имеетвид Ψ (x, t = 0) = Ax exp(− x ⁴ / 2), где x = x / / mω – безраз-

мерная координата осциллятора, A – постоянная. Какие значения энергии осциллятора можно обнаружить при измерениях?

А. только 3 ω / 2 Б. все нечетные собственные значения

В. все четные собственные значения Г. все собственные значения

248. Осциллятор находится в состоянии,в котором его энергияимеет определенное значение. Будет ли четность осциллятора иметь определенное значение в этом состоянии?

А. да Б. нет В. это зависит от состояния

Г. это зависит от энергии

249. Осциллятор находится в таком состоянии,в котором его энер-гия может принимать второе и восьмое собственные значения (ос-новное состояние – нулевое). Будет ли четность осциллятора иметь в этом состоянии определенное значение?

А. да, P = +1 Б. да, P = −1 В. нет Г. зависит от состояния

250. Осциллятор находится в состоянии,в котором его энергияимеет определенное значение. Будет ли координата осциллятора иметь в этом состоянии определенное значение?

А. да Б. нет

В. это зависит от состояния Г. это зависит от энергии

251. Осциллятор находится в состоянии,в котором его энергияимеет определенное значение. Будет ли импульс осциллятора иметь в этом состоянии определенное значение?

А. да	Б. нет	В. зависит от состояния
Г. зависит от энергии		n и m отличен от нуля инте-
252.Для каких значений индексов
грал	^+∞∫ f n (x) x ˆ f m (x) dx,где	f n (x)	и f m (x) – собственные функ-
	−∞
ции осциллятора, x ˆ – оператор координаты?
А. если индексы n и m совпадают
Б. если индексы n и m – числа одной четности

В. если индексы n и m отличаются на 2 Г. если индексы n и m отличаются на 1

253.Для каких значений индексов	n и m отличен от нуля инте-
грал ^+∞∫ f n (x) x ˆ ^2 f m (x) dx, где f n (x)	и f m (x) – собственные функ-
−∞

ции осциллятора, x ˆ – оператор координаты? А. только если индексы n и m совпадают

Б. если индексы n и m – числа одной четности

В. если индексы n и m совпадают или отличаются на 2 Г. только если индексы n и m отличаются на 2

254. Какой формулой(с точностью до безразмерного множителя)

определяется интеграл	^+∞∫ f n (x) x ˆ	f n +1(x) dx,где f n (x)	и f n +1(x) –
			−∞				x ˆ
нормированные собственные функции осциллятора,	– оператор
координаты?
А. ∼ / mω		Б. ∼ mω /
В. ∼ ω / m		Г. ∼ ω / m
255.Для каких значений индексов	n и	m отличен от нуля инте-
грал ^+∞∫ f n (x) p ˆ x	f m (x) dx,где f n (x)	и f m (x) – собственные функ-
	−∞
ции осциллятора, p ˆ x – оператор импульса?
А. если индексы n и m совпадают
Б. если индексы n и m отличаются на 1
В. если индексы n и m отличаются на 2
Г. если индексы n и m – числа одной четности
256.Для каких значений индексов	n и	m отличен от нуля инте-
грал	^+∞∫ f n (x) p ˆ x	^2 f m (x) dx,где	f n (x)	и f m (x) –	собственные
	−∞		p ˆ x –оператор импульса?
функции осциллятора,
А. только если индексы n и m совпадают

Б. только если индексы n и m отличаются на 2

В. если индексы n и m совпадают или отличаются на 2 Г. если индексы n и m – числа одной четности

257. Какой формулой(с точностью до безразмерного множителя)

определяется интеграл ^+∞∫	f n (x) p ˆ f n +1(x) dx,где f n (x)	и f n +1(x) –
−∞
нормированные собственные функции осциллятора, p ˆ	– оператор
импульса?
А. ∼ m / ω	Б. ∼ mω

В. ∼1/ mω Г. ∼ ω / m

258. Волновая функция осциллятора в момент времени t =0равна

А. (1 + x)exp(− x ² / 2) Б. (1 + x ²) exp(− x ² / 2)

В. (H ₀ (x) + H ₃ (x))exp(− x ² / 2) Г. x ⁴ exp(− x ² / 2),

где x = x / / mω – безразмерная координата осциллятора, H ₀(x)и H ₃(x)–нулевой и третий полиномы Эрмита.В каком из

этих состояний средняя координата осциллятора зависит от време-ни?

259. Волновая функция осциллятора в момент времени t =0равна

А. (1 + 2 x) exp(− x ² / 2) Б. (1 + 2 x ²) exp(− x ² / 2)

В. (H ₀ (x) + 2 H ₃ (x))exp(− x ² / 2) Г. 2 x ⁴ exp(− x ² / 2),

где x = x / / mω – безразмерная координата осциллятора, H ₀(x)и H ₃(x)–нулевой и третий полиномы Эрмита.В каком из

этих состояний средний импульс осциллятора зависит от времени? 260. Волновая функция осциллятора в момент времени t =0имеет

вид Ψ (x, t = 0) = A exp(− x ^2 / 2), где x = x /	/ mω – безразмер-
ная координата осциллятора,	A –постоянная.Как будет зависеть
от времени средний импульс осциллятора в этом состоянии?
А. не будет меняться	Б. будет расти
В. будет убывать	Г. будет осциллировать

261. Волновая функция осциллятора в момент времени t =0имеет

вид Ψ (x, t = 0) = A (1 + x) exp(− x ^2 / 2), где	x = x / / mω –без-
размерная координата осциллятора, A –	постоянная. Как будет

зависеть от времени средний импульс осциллятора в этом состоя-нии?

А. будет расти Б. будет убывать

В. не будет меняться Г. будет осциллировать

262. Волновая функция осциллятора в момент времени t =0имеетвид Ψ (x, t = 0) = A (1 + x) exp(− x ² / 2), где x = / mω – безраз-

мерная координата осциллятора, A – постоянная. Как будет зави-

сеть от времени средняя координата осциллятора в этом состоя-нии?

А. не будет меняться Б. будет расти

В. будет убывать Г. будет осциллировать

263. Волновая функция осциллятора в момент времени t =0имеетвид Ψ (x, t = 0) = A (1 + x) exp(− x ² / 2), где x = x / / mω – без-

размерная координата осциллятора, A – постоянная. С какой час-тотой будет осциллировать средняя координата осциллятора в этом состоянии как функция времени?

А. с частотой осциллятора Б. с удвоенной частотой осциллятора

В. с половинной частотой осциллятора Г. средняя координата осциллятора в рассматриваемом состоянии не зависит от времени

264. Волновая функция осциллятора в момент времени t =0имеет

вид Ψ (x, t = 0) = A (1 + x) exp(− x ^2 / 2), где	x = x / / mω –без-
размерная координата осциллятора, A –	постоянная. Как будет

зависеть от времени средняя энергия осциллятора в этом состоя-

нии?

А. не будет меняться Б. будет возрастать

В. будет убывать Г. будет осциллировать

265. Энергия осциллятора может принимать нулевое и второе соб-ственные значения. Как средний импульс осциллятора зависит от времени в рассматриваемом состоянии?

А. растет Б. убывает

В. осциллирует Г. не зависит от времени

266. Осциллятор находится в состоянии,в котором его энергияимеет определенное значение. Как средняя координата осциллято-ра зависит от времени в этом состоянии?

А. растет Б. убывает

В. не зависит от времени Г. осциллирует

267. Какие из перечисленных величин будут интегралами движе-ния для гармонического осциллятора?

А. координата Б. импульс

В. четность Г. никакие из перечисленных

268. Какой формулой может описываться волновая функция ос-

циллятора с частотой ω (x = x /	/ mω – безразмерная коорди-
ната осциллятора, A – постоянная)?
А. Ψ ( x , t ) = Ae − x ^2 / 2 e −3 iωt / 2	Б. Ψ (x, t) = Ae ^− ^x ^2 ^/ 2 e^i^ω^t ^/ 2
В. Ψ ( x , t ) = Axe − x ^2 / 2 e −3 iωt / 2	Г. Ψ ( x , t ) = Ax 2 e − x ^2 / 2 e −5 iωt / 2
269.Какой формулой может описываться волновая функция ос-
циллятора с частотой ω (x = x /	/ mω – безразмерная коорди-
ната осциллятора, A и B – постоянные)?

А. Ψ (x, t) = (Ae ^{− 3 i ω t / 2} + Bxe ^{− iωt / 2}) e ^{− x 2 / 2}

Б. Ψ (x, t) = (Ae ^{− iω t / 2} + Bxe ^{− 3 i ωt / 2}) e ^{− x 2 / 2}

В. Ψ (x, t) = (Ae ^{3 i ω t / 2} + Bxe ^{iωt / 2}) e ^{− x 2 / 2}

Г. Ψ (x, t) = (Ae ^{iω t / 2} + Bxe ^{3 i ωt / 2}) e ^{− x 2 / 2}

270. Какая из перечисленных функций является волновой функци-ей Ψ(x, t) стационарного состояния осциллятора (x = x / / mω

– безразмерная координата осциллятора, A – постоянная)?

А. Ψ (x, t) Б. Ψ (x, t) В. Ψ (x, t)

Г. Ψ (x, t)

_{= Ae} − x ² / 2

_{= Axe} − x ² / 2 _e 3 iωt / 2

_{= A ( e} − x ² / 2 _e − iω t / 2 _{+ xe} − x ² / 2 _e −3 iωt / 2 ₎

_{= Axe} − x ² / 2 _e −3 iωt / 2

271. Осциллятор находится в стационарном состоянии. При изме-рении энергии осциллятора могут быть получены А. единственное значение с единичной вероятностью Б. два значения с одинаковыми вероятностями В. три значения с одинаковыми вероятностями Г. это несвязанные вещи

272. Осциллятор находится в n -м стационарном состоянии. Как средний импульс осциллятора зависит от n?

А. растет Б. убывает В. не зависит от n

Г. при малых n растет, при больших – убывает.

273.Осциллятор находится в	n -м стационарном состоянии.Как
величина	x 2		зависит от n?
А. не зависит	Б. как	n	В. как n
Г. как n ^2

Дата добавления: 2014-12-24