Сферический осциллятор, кулоновский потенциал и бесконечно глубокая сферическая потенциальная яма 1 страница

461. В каких двух из перечисленных ниже четырех центральныхпотенциалов существует вырождение стационарных состояний дискретного спектра по моменту?

А. U (r) = αr	Б. U (r) = αr ^2
В. U (r) =	α	Г. U (r) =	α
	r		r 2

462. Какой формулой исчерпываются энергии всех стационарныхсостояний сферического осциллятора (N = 0,1, 2,...)?

А.	ω (N +1/ 2)	Б.	ω (N +3/ 2)
В.	ω (N +5 / 2)	Г.	ω (N +7 / 2)

463. Чему равна энергия основного состояния сферического осцил-лятора с частотой ω?

А.	1	ω	Б. ω	В.		ω	Г. 2 ω

464. Какова кратность вырождения первого возбужденного состоя-

ния сферического осциллятора?
А. 1	Б. 2	В. 3	Г. 4

465. Какова кратность вырождения второго возбужденного состоя-ния сферического осциллятора?

А. 3 Б. 4 В. 5 Г. 6

466. Кратность вырождения первого возбужденного состояниясферического осциллятора равна 3. На основе этих данных срав-

^нить ^En =0 l =1	^и ^En =1 l =0	(нумерация nr начинается от нуля).
r		r
^А^. ^E n =0 l =1	^> ^En =1 l =0	^Б^. ^E n =0 l =1	^< ^En =1 l =0
r		r	r	r
^В^. ^E n =0 l =1	^= ^En =1 l =0	Г. данные условия и соотно-
r		r

шение указанных энергий никак не связаны между собой 467. Кратность вырождения первого возбужденного состояния

сферического осциллятора равна 3, второго – 6. На основе этих данных сравнить E_{nr =0 l =2} и E_{nr =2 l =0} (нумерация n_r начинается от нуля)

^А^. ^E n =0 l =2	^> ^En =2 l =0	^Б^. ^E n =0 l =2	^< ^En =2 l =0
r	r	r	r
^В^. ^E n =0 l =2	^= ^En =2 l =0	Г. данные условия и соотно-
r	r

шение указанных энергий никак не связаны между собой 468. Сферический осциллятор имеет«декартовые»квантовые чис-

ла n _x = 2, n _y = 3, n_z = 4. Чему равна энергия осциллятора?

А.	19	ω	Б.	21	ω	В.	23	ω	Г.	25	ω

469. Волновая функция основного состояния сферического осцил-лятора это

А. C exp(− r ² / 2 a ²) Б. C exp(− r / a)

В. C exp(− r / 2 a) Г. C exp(− r ² / a ²)

(C – нормировочная постоянная, a = / mω)

470. Сферический осциллятор находится в стационарном состоя-нии с волновой функцией xye ^{− ( x 2 + y 2 + z 2 ) / 2} (x, y, z – безразмерные

декартовые координаты осциллятора). Каковы «декартовые» кван-товые числа этого состояния осциллятора?

А. n _x = 0, n _y = 0, n_z = 2 Б. n _x =1, n _y = 1, n_z = 0

В. n _x = 2, n _y = 2, n_z = 0 Г. n _x =1, n _y = 1, n_z = 3

471. Сферический осциллятор находится на втором возбуж-денном уровне энергии. Перечислить все значения момента импульса, которые можно обнаружить при измерениях.

Указание: кратность вырождения второго возбужденного уровня энергии сферического гармонического осциллятора равна 6.

А. l =1 и l = 2 Б. l = 0 и l =1

В. l = 0 и l = 2 Г. l = 2

472. Сферический осциллятор находится на первом возбужденномуровне энергии. Какова вероятность того, что проекция момента

осциллятора на ось z	равна m = −1?
А. 1/3	Б. 2/3
В. 0	Г. это зависит от состояния

473. Сферический осциллятор находится в состоянии с«декарто-выми» квантовыми числами n _x =1, n _y = 0, n_z = 0. Какие значения

момента импульса можно получит при измерениях?

Указание: кратность вырождения первого возбужденного уровня энергии сферического гармонического осциллятора равна 3.

А. l =1 Б. l = 0

В. l =1 и l = 2 Г. l = 2 и l = 3

474. Сферический осциллятор находится в состоянии с«декарто-выми» квантовыми числами n _x = 0, n _y = 1, n_z = 0. Какие значения

проекции момента импульса на ось z можно получить при изме-рениях?

А. m = 0 Б. m =1

В. m =1 и m = −1 Г. m = 2 и m = −2

475. Сферический осциллятор находится в состоянии с«декарто-выми» квантовыми числами n _x = 0, n _y = 0, n_z =1. Какие значения

проекции момента импульса на ось z можно получить при изме-рениях?

А. m = 0 Б. m =1

В. m =1 и m = −1 Г. m = 2 и m = −2

476. Сферический осциллятор находится в состоянии с«декарто-выми» квантовыми числами n _x = 0, n _y = 0, n_z = 2008. Какие зна-

чения проекции момента импульса на ось z можно получить при измерениях?

А. m = 0 Б. m = 2008 и m = −2008

В. m = 2008 Г. все значения от m = 0 до m = 2008

477. Сферический осциллятор находится на первом возбужденномуровне энергии. Какой формулой не может описываться зависи-мость его волновой функции от полярного и азимутального углов

ϑ и ϕ?

Указание: кратность вырождения первого возбужденного уровня энергии сферического гармонического осциллятора равна 3.

А. sin ϑ sin ϕ Б. cos ϑ

В. sin ϑ exp(− iϕ) Г. cos ϑ cos ϕ

478. Сферический осциллятор находится на втором возбужденномуровне энергии в состоянии с моментом l = 2. Сколько узлов име-ет радиальная волновая функция электрона χ (r), включая узел

при r = 0 (Ψ (r, ϑ, ϕ) = R (r) Y_lm (ϑ, ϕ), R (r) = χ (r) / r)?

А. 1 Б. 2 В. 3 Г. 4

479. Сферический осциллятор находится в стационарном состоя-нии. Будет ли четность осциллятора иметь определенное значение? А. да Б. нет В. зависит от состояния Г. только если осциллятор находится в основном или первом воз-бужденном состоянии

480. Боровский радиус–это(μ –масса электрона, e –его заряд, c –скорость света)

А.			e ^2
	Б.			В.			Г.
μc ^2	μ		e ^2 c		μe ^2

481. Электрон находится в водородоподобном ионе с зарядом ядра Z. Как боровский радиус зависит от Z?

А. как Z	Б. как Z	В. как		Г. как
Z	Z

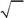
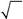482. Какая из четырех нижеперечисленных величин является атом-ной единицей энергии (μ – масса электрона, e – его заряд)?

А.	μe ^2	Б.		В.	μe ^4	Г.
	μe ^2		μe ^4

483. Какой формулой исчерпываются энергии всех стационарныхсостояний электрона в атоме водорода (N =1, 2,3,..., μ – масса электрона, e – его заряд)?

А. −	μe ^4			Б. −	μe ^4
N ^2			N
В. −		μe ^4	Г. −	μe ^4
	2 N ^2		2 N

484. Волновая функция основного состояния электрона в атоме во-дорода это

А. C exp(− r / a) Б. Cr exp(− r / a) В. C exp(− r / 2 a)

Г. Cr exp(− r / 2 a)

(C – нормировочная постоянная, a – боровский радиус).

485. Электрон находится в основном состоянии атома водорода,тоесть его состояние описывается волновой функцией C exp(− r / a)

(C – нормировочная постоянная,	a –боровский радиус).Каково
наиболее вероятное расстояние от электрона до ядра?
А. rн . в . = 0	Б. rн . в . = a / 2	В. rн . в . = a
Г. rн . в . = 2 a

486. Электрон в атоме водорода находится в стационарном состоя-нии. Будет ли момент импульса электрона иметь определенное зна-чение?

А. да Б. нет В. это зависит от состояния Г. это зависит от гамильтониана электрона

487. Для электрона в атоме водорода сравнить E_{nr =4 l =3}и E_{nr =5 l =2}.

^А^. ^E n =4 l =3	^> ^En =5 l =2	^Б^. ^E n =4 l =3	^< ^En =5 l =2
r	r	r	r
^В^. ^E n =4 l =3	^= ^En =5 l =2	Г. это зависит от m
r	r

488. Для электрона в атоме водорода сравнить E_{nr =0 l =3}и E_{nr =1 l =4}.

^А^. ^E n =0 l =3	^> ^En =1 l =4	^Б^. ^E n =0 l =3	^< ^En =1 l =4
r	r	r	r
^В^. ^E n =0 l =3	^= ^En =1 l =4	Г. зависит от m
r	r

489. Какие ортогональные многочлены определяют радиальные волновые функции стационарных состояний электрона в атоме во-дорода?

А. полиномы Лежандра Б. полиномы Лагерра

В. присоединенные полиномы Лежандра Г. полиномы Эрмита

490. Электрон в атоме водорода находится в стационарном состоя-

нии с квантовыми числами n_r, l и m (n_r – радиальное квантовое

число,	l –момент и m –проекция момента).От каких квантовых
чисел	зависит радиальная волновая функция R (r)	электрона
(Ψ (r, ϑ, ϕ) = R (r) Ylm (ϑ, ϕ))?
А. функция R (r) зависит от всех квантовых чисел nr, l	и m

Б. функция R (r)	зависит от nr, но не зависит от l и m
В. функция R (r)	зависит от nr и l, но не зависит от m
Г. функция R (r)	зависит от l и m, но не зависит от nr

491. Электрон в атоме водорода находится в стационарном состоя-нии. Будет ли четность этого состояния иметь определенное значе-

ние?

А. да Б. нет В. это зависит от состояния

Г. да, если электрон на первом возбужденном уровне энергии

492. В каких пределах может меняться момент l стационарногосостояния электрона в атоме водорода при фиксированном ради-

альном квантовом числе n_r этого состояния?

А. любое целое число из интервала значений 0 ≤ l ≤ n_r −1 Б. любое целое число из интервала значений 0 ≤ l ≤ n_r В. любое целое число из интервала значений 0 ≤ l ≤ n_r +1

Г. любое целое неотрицательное число 493. Какой формулой определяется энергия стационарного состоя-

ния с квантовыми числами n_r, l и m электрона в атоме водорода (n_r – радиальное квантовое число, l – момент и m – проекция мо-

мента; нумерация nr	начинается с единицы)?
А. −	e ^2	Б. −	e ^2
2 a (n + l)^2			2 a (n + l +1)^2
		r		r
В. −		e ^2	Г. −	e ^2
	2 a (n + l + m)^2		2 a (n + l + m +1)^2
		r		r

494. Электрон в атоме водорода находится в состоянии с кванто-выми числами n_r = 4, l = 6, m = 2 (нумерация n_r начинается с ну-ля). Сколько узлов имеет радиальная волновая функция (без учета

узла при r = 0)
А. 4	Б. 6	В. 2	Г. 12

495. Радиальная волновая функция электрона,находящегося в ста-ционарном состоянии в атоме водорода имеет пять узлов. Чему ра-вен момент импульса электрона?

А. l = 4 Б. l = 5 В. l = 6

Г. это несвязанные вещи 496. Какова кратность вырождения третьего возбужденного уровня

энергии электрона в атоме водорода?
А. 9	Б. 16	В. 25	Г. 36

497. Какова кратность вырождения уровня энергии^{− me 4}элек-

32 ²

трона в атоме водорода?

А. 4 Б. 9 В. 16 Г. 25

498. Электрон находится на первом возбужденном уровне энергииатома водорода. Измеряют момент импульса электрона. С какой вероятностью будет получено значение l =1?

А. w =1/ 4 Б. w = 3/ 4 В. w = 0

Г. это зависит от состояния

499. Электрон находится на первом возбужденном уровне энергииатома водорода. Какой функцией не может описываться зависи-мость его волновой функции от углов?

А. sin ϑ cos ϕ Б. cos ϑ + sin ϑe ^{− iϕ} В. cos ϑ cos ϕ Г. sin ϑ (cos ϕ − 2sin ϕ)

500. Электрон находится на втором возбужденном уровне энергииатома водорода. Перечислите все значения момента импульса, ко-торые можно обнаружить при измерениях

А. l = 0, l =1 и l = 2 Б. l = 0, l = 2 и l = 4

В. l =1 и l = 3 Г. l = 0 и l = 2

501. Электрон находится на третьем возбужденном уровне энергииатома водорода. Перечислите все значения проекции момента им-пульса на ось z, которые можно обнаружить при измерениях.

А. lz = −,	0,
Б. только значение lz	=
В. lz = −2,	, 0,		, 2
Г. lz = − 3, − 2,	,	0,, 2, 3

502. Какие значения момента импульса отвечают10-му возбуж-денному уровню энергии электрона в атоме водорода?

А. все четные от l = 0 до l =10 Б. все нечетные от l =1 до l =11

В. все возможные от l = 0 до l =10 Г. все возможные от l = 0 до l =11

503. Электрон в атоме водорода с вероятностью1/4находится всостоянии с квантовыми числами n_r = 3, l = 0, а с вероятностью 3/4 – в состоянии с квантовыми числами n_r = 2, l =1. Будет ли

состояние электрона стационарным? А. да Б. нет

В. зависит от значений магнитного квантового числа Г. в некоторых случаях будет, в некоторых нет.

504. Электрон в атоме водорода с вероятностью1/4находится всостоянии с квантовыми числами n_r = 3, l = 0, а с вероятностью 3/4 – в состоянии с квантовыми числами n_r =1, l =1. Будет ли со-

стояние электрона стационарным? А. да Б. нет

В. зависит от значений магнитного квантового числа Г. в некоторых случаях будет, в некоторых нет.

505. Волновая функция электрона в атоме водорода в момент вре-мени t = 0 равна C exp(− r / a) (C – нормировочная постоянная,

a –боровский радиус).Какой формулой описывается волноваяфункция электрона в любой момент времени?

	−	ime ^4 t
А. C exp(− r / a) e
−	ime ^4 t
Б. C exp(− r / a) e
	ime ^4 t
В. C exp(− r / a) e

Г. аналитически найти решение временного уравнения Шредингера для такого начального условия не удается

506. Какой формулой определяются энергии s -состояний частицымассой μ в сферической бесконечно глубокой прямоугольной по-

тенциальной яме радиуса a (n =1, 2,3...)?

_π 2 2 _n 2

^А. 2 μ (2 a)²

π ^{2 2} n

^В. _{2 μ a} 2

_π 2 2 _n 2

^Б. _{2 μ a} 2

π ^{2 2} n

^Г. 2 μ (2 a)²

507. Какой формулой определяются волновые функции стационар-ных состояний с l = 0 для частицы, находящейся в сферической бесконечно глубокой прямоугольной потенциальной яме (k – не-которое число)?

А. ψ (r) ∼ sin kr / r внутри ямы и ψ (r) = 0 снаружи Б. ψ (r) ∼ cos kr / r внутри ямы и ψ (r) = 0 снаружи В. ψ (r) ∼ exp(− kr) / r внутри ямы и ψ (r) = 0 снаружи Г. ψ (r) ∼ exp(ikr) / r внутри ямы и ψ (r) = 0 снаружи

Дата добавления: 2014-12-24