Сферический осциллятор, кулоновский потенциал и бесконечно глубокая сферическая потенциальная яма 5 страница

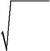
А.

Б.

2 mα

2 mα

В.

Г.

2 mα

2 mα

586. Частица движется в потенциале U (x)= _x^α ₂(α <0).При ка-

ких значениях координаты лучше работает квазиклассическое при-ближение, если энергия частицы равна нулю?

А. при малых, так как потенциальная энергия – резкая функция ко-ординаты при малых x

Б. при больших, так как потенциальная энергия – плавная функция при больших x

В. при любых одинаково, так как параметр квазиклассичости не зависит от координат Г. это зависит от параметра α.

587. Решают уравнение Шредингера при энергии E в потенциалах,изображенных на рисунках (энергия показана черточкой на оси по-тенциалов). Для какого случая можно ожидать лучшей работы ква-

зиклассического приближения?
А. для левого	Б. для правого
В. одинаково	Г. мало информации, чтобы ответить
	U (x)	E		U (x)	x
E	x

588. Какая из функций является квазиклассическим решением ста-ционарного уравнения Шредингера в потенциале U (x) при энер-

гии E при таких значениях координаты, когда E > U (x)?

C

exp (− ik (x) x)

x

А.

Б. C

k (x) exp− i

∫

k (t) dt

k (x)

a

C

x

C

x

В.

exp

− i

∫

k (t) dt

Г.

exp

−

∫

| k (t) | dt

k (x)

| k (x) |

a

a

(k ^2 (x) = 2 m (E − U (x))/

^2, m – масса частицы, C и a – числа)

589. Какая из функций является квазиклассическим решением ста-ционарного уравнения Шредингера в потенциале U (x) при энергии

E при таких значениях координаты,когда E < U (x)?

	C			x
А.		exp	−	∫	| k (t) | dt
	| k (x) |
			a
				x
В. C k (x) exp − i	∫	k (t) dt
				a

(k ² (x) = 2 m (E − U (x))/ ², m

	C				x
Б.	exp	− i	∫	k (t) dt
	k (x)
				a
Г.	C		exp (− | k (x) | x)
| k (x) |

– масса частицы, C и a – числа)?

590.Включение множителя1/	k (x)	в квазиклассическое решение
уравнения Шредингера
	x			C		x
C exp i	∫	k (t) dt	→		exp i	∫	k (t) dt
			k (x)
	a				a

приводит к тому, что А. эта функция перестает быть решением

Б. изменяется начало отсчета координаты В. эта функция остается решением в том же порядке по параметру квазиклассичности

Г. учитывается следующий порядок по параметру квазиклассично-сти

591.Включение множителя	k (x)в квазиклассическое решение
уравнения Шредингера
	x				x
C exp i	∫	k (t) dt	→ C k (x) exp i	∫	k (t) dt
	a				a

приводит к тому, что А. эта функция перестает быть решением

Б. изменяется начало отсчета координаты В. эта функция остается решением в том же порядке по параметру квазиклассичности

Г. учитывается следующий порядок по параметру квазиклассично-сти

592. К чему приведет изменение нижнего предела интегрирования a → a 'в общем квазиклассическом решении уравнения Шредин-

	C	^x			D	^x
гера ψ (x) =	sin	k (t) dt	+	cos	k (t) dt?
	k (x)	∫			k (x)	∫
	a			a

А. к тому, что эта функция перестанет быть решением Б. к изменению произвольных постоянных C и D В. к выходу в область неквазиклассичности Г. к изменению начала отсчета времени

593. Частица массой m движется в потенциале U (x)= αx. Какой

формулой определяется квазиклассическое решение уравнения
Шредингера при энергии E (в области, где E > αx)?
А. C exp (± ib (E − αx)^3 / 2)	Б.	C exp(± ib (E − αx)^5 / 2)
В. C exp (± ib (E − αx)^7 / 2)	Г.		C exp(± ib (E − αx)^9 / 2)
(где C – произвольная постоянная, b =		4 m			)
	3 α ^2
594.Частица движется в потенциале U (x)=		α	(α < 0). Какой
	x 2

формулой определяются квазиклассические решения уравнения Шредингера при энергии частицы, равной нулю?

А. sin α x и cos αx	Б. e ^− α ^x и e^α^x
В. | x | ^i ^α и | x |^− ^i ^α	Г. | x | ^α и | x |^− α

595. Для каких потенциалов квазиклассическое решение уравненияШредингера совпадает с точным?

А. только для U (x) = const

Б. только для: U (x) = const и U (x) ∼ x ²

В. только для: U (x) = const, U (x) ∼ x ² и U (x) ∼ x

Г. ни для какого из этих потенциалов 596. Рассматриваем решение стационарного уравнения Шрединге-

ра для частицы массой m в потенциале U (x) при энергии E. Из

какого уравнения можно найти такие значения координат, при ко-торых квазиклассическое приближение не работает?

А. E = U ′(x)

В. E = U (x)

	2 m		3 / 2		′
Б.			E		= U (x)
				− 3 / 2	′
Г.		E			= U (x)
2 m

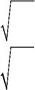
597. График потенциальной

энергии частицы имеет вид, по-		U (x)
казанный на рисунке. Решается
уравнение	Шредингера при	a	b	c
энергии E (показана на рисун-	d
ке горизонтальной пунктирной						x
прямой в том масштабе, кото-				E
рый принят	для оси потенци-

альной энергии). При каких значениях координат можно ожидать, что квазиклассическое приближение будет работать?

А. точность квазиклассического приближения от координат не за-висит

Б. а < x < c

В. a < x < b,	c < x < d
Г. x < a, b < x < c,	x > d
598.График потенциальной энер-		U (x)
гии частицы имеет вид, показан-
ный на рисунке (потенциальные		E
стенки при	x = a и	x = b верти-	a	b
кальны). Будет ли квазиклассиче-	x
ское решение уравнения Шредин-
гера при энергии E (показана на
рисунке горизонтальной пунктир-
ной прямой в том масштабе, кото-

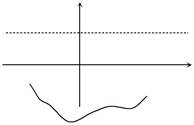рый принят для оси потенциальной энергии) работать в окрестно-стях точек поворота x = a и x = b?

А. да Б. нет

В. в окрестности точки x = a – да, в окрестности x = b – нет Г. в окрестности точки x = b – да, в окрестности x = a – нет

599.	Уравнение	Шредингера
решается в потенциале, график	U (x)
которого изображен на рисун-
ке (в	точке x = a потенциал			E
имеет	вертикальную	стенку
конечной высоты). Энергия,	a		x
для которой решается уравне-
ние,	показана	на	рисунке

пунктирной горизонтальной прямой. Как установить условия сшивки квазиклассических решений справа и слева от точки пово-рота x = a?

А. обходя точку поворота в комплексной плоскости энергии Б. заменяя потенциал линейной функцией

В. приравнивая друг к другу значения квазиклассических функций и их производные в самой точке поворота Г. при таком разрыве потенциала «сшить» квазиклассические функции невозможно

600. Квазиклассическое приближение работает,если действие S,которое имела бы частица, если бы она двигалась по законам клас-сической механики в данном потенциале при данной энергии, было А. S Б. S В. S m Г. S E

где m – масса частицы, E – ее энергия

601. Из квазиклассических решений уравнения Шредингера следу-ет, что решение при E > U (x) является

А. растущей или затухающей функцией Б. осциллирующей функцией В. постоянной

Г. это зависит от E

602. Из квазиклассических решений уравнения Шредингера следу-ет, что решение при E < U (x) является

А. растущей или затухающей функцией Б. осциллирующей функцией В. постоянной

Г. это зависит от E

603. «Так как в точках поворота k (x)=0,то в этих точках квази-классические решения уравнения Шредингера, содержащие k (x)

в знаменателе, расходятся. Следовательно, классические точки по-ворота являются особыми точками решений уравнения Шрединге-ра». Правильно ли это утверждение?

А. да, так как оно использует свойства приближенных квазииклас-сических решений Б. нет, так как в окрестности точек поворота квазиклассические

решения не имеют ничего общего с истинными решениями В. это зависит от энергии

Г. это зависит от поведения потенциальной энергии в окрестностях точек поворота

604. Что позволяют «условия сшивки» квазиклассических функ-

ций?

А. установить соотношения между постоянными в квазиклассиче-ском решении справа и слева от точек остановки классического движения Б. связать квазиклассическое решение вдали от точек остановки с

точным решением в окрестности точек остановки В. связать решения справа и слева от особых точек потенциала

Г. найти значения квазиклассических функций в точках остановки

605. Какая формула представляет собой условие сшивки квазиклас-сических функций слева и справа от точки остановки?

А.

Б.

В.

Г.

2 C

^x

π

C

^a

cos

∫

k (t) dt +

↔

sin

k (t) dt

k (x)

k (x)

∫

a

x

x

^a

2 C

− ∫ k (t) dt

C

∫ k (t) dt

e a

↔

e x

k (x)

k (x)

x

a

∫ k (t) dt

2 C

− i ∫ k (t) dt

C

i

ea

↔

e

x

k (x)

k (x)

x

2 C

^a

π

C

− ∫| k (t)| dt

cos

∫

k (t) dt −

↔

e

a

k (x)

| k (x) |

x

Дата добавления: 2014-12-24