Теория возмущений без вырождения 2 страница

ной потенциальной яме, расположенной между точками	x =0и
x = a,наложили возмущение αδ (x − a / 2),где δ (...)	– δ -

функция. Каким должен быть параметр α, чтобы для расчета энер-гий можно было пользоваться теорией возмущений?

А. α			Б. α	m 2	В. α	ma
	ma		a
Г. α		m
a ^2

631. На частицу,находящуюся в бесконечно глубокой прямоуголь-

ной потенциальной яме, расположенной между точками	x =0и
x = a,наложили возмущение αδ (x − a / 2),где δ (...)	– δ -

функция. Для каких уровней – с большими или малыми квантовы-ми числами – лучше работает теория возмущений?

А. для больших Б. для малых В. безразлично Г. для такого возмущения пользоваться теорией возмущений нель-зя.

632. На частицу,находящуюся в бесконечно глубокой прямоуголь-

ной потенциальной яме, расположенной между точками	x =0и
x = a,наложили малое возмущение V (x)= V 0 x (a − x)	(V 0 > 0).

Как изменятся энергии стационарных состояний в первом порядке теории возмущений по сравнению с невозмущенной задачей?

А. увеличатся Б. уменьшатся В. не изменятся Г. зависит от размера ямы

633. На частицу,находящуюся в бесконечно глубокой прямоуголь-ной потенциальной яме, расположенной между точками x = 0 и x = a,наложили малое возмущение V (x)= V ₀(x − a / 2)(V ₀>0).

Как изменятся энергии стационарных состояний в первом порядке теории возмущений по сравнению с невозмущенной задачей?

А. увеличатся Б. уменьшатся В. не изменятся

Г. зависит от размера ямы

634. На частицу массой m,находящуюся в бесконечно глубокойпрямоугольной потенциальной яме шириной a, наложили малое возмущение V (x) = V ₀ x (x − a). При каком условии на величину V ₀

для расчета возмущенных энергий и волновых функций стацио-нарных состояний можно пользоваться теорией возмущений?

А. V 0			Б. V 0		В. V 0
	ma	ma ^2	ma ^3
Г. V 0
ma ^4

635. На частицу,находящуюся в бесконечно глубокой прямоуголь-ной потенциальной яме, расположенной между точками x = 0 и

x = a,наложили малое возмущение V (x)= V ₀sin²(2 π x / a),где

V ₀>0.Как изменятся энергии стационарных состояний в первом

порядке теории возмущений?

А. увеличатся Б. уменьшатся В. не изменятся Г. зависит от размера ямы

636. На частицу,находящуюся в бесконечно глубокой прямоуголь-ной потенциальной яме, расположенной между точками x = 0 и

x = a,наложили малое возмущение V (x)= V ₀sin²(2 π x / a),где

a –размер ямы.Какой формулой определяется поправка третьегопорядка к энергии уровней?

E (3)

V ^3 ma ^2

E (3)

V ^3 m ^2 a ^4

А.

∼

Б.

∼

E (3)

V ^3

E (3)

V ^3

В.

∼

Г.

∼

ma ^2

m 2 a 4

637. На частицу,находящуюся в бесконечно глубокой прямоуголь-ной потенциальной яме, расположенной между точками x = 0 и x = a,наложили возмущение V (x)= V ₀sin(π x / a),где V ₀>0.Как изменятся энергии стационарных состояний в первом порядке теории возмущений?

А. увеличатся Б. уменьшатся В. не изменятся Г. зависит от размера ямы

638. На частицу,находящуюся в бесконечно глубокой прямоуголь-ной потенциальной яме, расположенной между точками x = 0 и x = a,наложили малое возмущение V (x)= V ₀ f (x),где V ₀–неко-торое число. Как поправки второго порядка теории возмущений к энергиям стационарных состояний зависят от V ₀?

А.	E ^(2)∼ V 0	Б. E ^(2) ∼ V 0^2	В. E ^(2) ∼ V 0^−^2
Г.	E ^(2)∼ V 0^−^1

639. На частицу,находящуюся в бесконечно глубокой прямоуголь-ной потенциальной яме, расположенной между точками x = 0 и x = a,наложили малое возмущение V (x)= V ₀cos(π x / a).Сколь-

ко ненулевых слагаемых входит в формулу для поправки второго

порядка к энергии основного состояния?
А. 1	Б. 2	В. 3	Г. бесконечно много

640. На частицу,находящуюся в бесконечно глубокой прямоуголь-ной потенциальной яме, расположенной между точками x = 0 и x = a,наложили малое возмущение V (x)= V ₀cos(π x / a).Сколь-

ко ненулевых слагаемых входит в формулу для поправки второго порядка к энергии 99-го стационарного состояния?

А. 1 Б. 2 В. 99 Г. бесконечно много

641. На частицу,находящуюся в бесконечно глубокой прямоуголь-ной потенциальной яме, расположенной между точками x = 0 и

x = a,наложили малое возмущение V (x)= V ₀cos(π x / a).Чемуравна поправка второго порядка к энергии основного состояния?

А.	E (2)	= −	V ^2 ma ^2	Б.	E (2)	= −	V ^2 ma ^2
			6 π ^2					12 π ^2
В.	E (2)	= −	V ^2 ma ^2	Г.	E (2)	= −	V ^2 ma ^2
			3 π ^2					8 π ^2

642. На частицу,находящуюся в бесконечно глубокой прямоуголь-ной потенциальной яме, наложили произвольное возмущение V (x).Как поправка первого порядка к энергии n -го стационарно-

го состояния зависит от квантового числа n при больших значени-ях n?

А. растет с ростом n Б. убывает с ростом n

В. не зависит от n Г. это зависит от размера ямы

643. На одномерный гармонический осциллятор массой m и час-

тотой	ˆ
ω накладывают малое возмущение V (x)= V 0sin(x / b).Ка-

ким будет сдвиг энергий стационарных состояний осциллятора в первом порядке теории возмущений?

А.	E =0			Б. E = V	В. E = ^V ^0
				b mω
		V 0
Г.	E =
b ^2		mω

644. На одномерный гармонический осциллятор накладывают ма-

	ˆ	Увеличится или уменьшится
лое возмущение V (x) = a sin(x / b).
при этом энергия основного состояния осциллятора?
А. увеличится	Б. уменьшится	В. не изменится

Г. это зависит от знака параметра a

645. На одномерный гармонический осциллятор наложили малое

возмущение ^ˆ = αδ, где δ (...) – ^δ -функция. Как изменятся

V (x) (x)

энергии нечетных уровней осциллятора (уровень с самой малень-кой энергией – нулевой)?

А. увеличатся Б. уменьшатся В. не изменятся Г. зависит от уровня

646. На одномерный гармонический осциллятор наложили возму-

ˆ	δ (...)–	δ -функция.Как поправка пер-
щение V (x) = αδ (x), где

вого порядка теории возмущений к энергии четных стационарных

состояний зависит от квантового числа состояния для больших значений квантового числа?

А. как		Б. как	1	В. как
n	n	n ^2

Г. не зависит от n

647. На одномерный гармонический осциллятор наложили возму-

щение ^ˆ = αδ, где δ (...) – ^δ -функция. Для каких уровней –

V (x) (x)

с большими или малыми квантовыми числами – лучше работает теория возмущений?

А. с малыми Б. с большими

В. не зависит от номера уровня Г. такое возмущение нельзя учитывать по теории возмущений

648. На одномерный гармонический осциллятор наложили возму-

	ˆ	= αδ (x), где δ (...) –	δ -функция.При каких значени-
щение V (x)
ях параметра α это возмущение можно считать малым?
А. α	ωa	Б. α		ωa	В. α	ω
	a
Г. α	ω		(здесь a =		)
a	mω

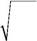649. На одномерный гармонический осциллятор наложили возму-

		ˆ		δ (...)– δ -функция.Какой формулой
щение V (x) = αδ (x), где
определяется поправка четвертого порядка к энергиям уровней?
А.	E	(4)	∼	α ^4 m	Б.	E	(4)	∼	α ^4 m ^3
			4 2
				ω					ω
В.	E	(4)	∼	α ^4 m ^2	Г.	E	(4)	= 0
				ω

650. На одномерный гармонический осциллятор наложили возму-

щение ^ˆ = α. Сколько ненулевых слагаемых будут ходить в

V (x) x

формулу для поправки второго порядка к энергии n -го стационар-

ного состояния (n ≠ 0)?	В. n
А. одно	Б. два

Г. бесконечно много 651. На одномерный гармонический осциллятор наложили малое

возмущение ^ˆ = α. Каким будет сдвиг энергии основного со-

V (x) x

стояния осциллятора в первых двух порядках теории возмущений?

А.

E = −

α 2

Б.

E = α

−

α 2

2 3

mω

2 m ω

4 m ω

В.

E = −

α ^2

Г.

E = α

−

α ^2

2 3

mω

2 3

8 m ω

16 m

ω

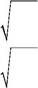Указание. Матричный элемент оператора координаты с волновыми функциями основного ϕ ₀ (x) и первого возбужденного ϕ ₁(x) ста-ционарных состояний гармонического осциллятора равен

∫ ^ϕ 0 ^{( x ) xϕ} 1 ^{( x ) dx =} _{2 m ω} ^.

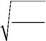
652. На одномерный гармонический осциллятор накладывают ма-

ˆ			. Как поправки теории возмущений к
лое возмущение V (x) = ax
энергии n -го уровня энергии зависят от n?		1
А как n	Б. как n ^2	В. как
					n

Г. не зависят от n

653. На одномерный гармонический осциллятор накладывают ма-

ˆ	f (x),где	f (x)–некоторая функция
лое возмущение V (x) = V 0

координаты, V ₀ – параметр, имеющий размерность энергии. Как поправки второго порядка теории возмущений к энергиям уровней

осциллятора зависят от V 0?
А как V	Б. как V ^2	В. как V ^3	Г. как V ^4

654. На одномерный гармонический осциллятор наложили малое

	ˆ				. Какой формулой определяется поправка
возмущение V (x) = αx
второго порядка к энергиям стационарных состояний?
А. E ^(4) ∼	α ^2				Б. E ^(4) ∼	α ^2
mω					ω
					m

В. E ^(4) ∼	α ^2	2	Г. E ^(4) ∼	α ^2
	m ω			m ω

655. На одномерный гармонический осциллятор наложили возму-

	ˆ		. При каких условиях на α	для расчета влияния
щение V (x) = αx
этого возмущения можно использовать теорию возмущений?
А. α			m 5 ω 6			Б. α	m 4 ω 6
В. α			m 3 ω 4			Г. α	m 2 ω 3

656. На одномерный гармонический осциллятор накладывают ма-

лое возмущение ^ˆ =. Как поправка первого порядка

V

)

b

/

x

cos(

a

)

x

(

теории возмущений к энергии основного состояния зависит от b?

А увеличивается с ростом b Б. убывает с ростом b

В. не зависит от b Г. равна нулю

657. На трехмерный гармонический осциллятор наложили малое

			ˆ
возмущение V (x, y, z) = αx. Чему равен сдвиг энергии основного
состояния осциллятора в первом порядке теории возмущений?
А.	E (1)	= α					Б.	E ^(1)= − α
		2 mω	mω
В.	E (1)	= α					Г.	E ^(1)=0
		mω

658. На атом водорода накладывают однородное электрическое по-ле с напряженностью E. Чему равен сдвиг энергии основного со-стояния электрона в первом порядке теории возмущений

Дата добавления: 2014-12-24