Сферический осциллятор, кулоновский потенциал и бесконечно глубокая сферическая потенциальная яма 6 страница

606. Квазиклассическое правило квантования дает возможность спомощью квазиклассического решения стационарного уравнения Шредингера найти:

А. собственные функции оператора Гамильтона, отвечающие не-прерывному спектру Б. собственные значения оператора Гамильтона, отвечающие не-прерывному спектру

В. собственные функции оператора Гамильтона, отвечающие дис-кретному спектру Г. собственные значения оператора Гамильтона, отвечающие дис-кретному спектру

607. Для каких уровней энергии выше точность квазиклассическогоправила квантования А. с маленькими квантовыми числами

Б. с большими квантовыми числами В. для уровней, энергия которых много больше постоянной Планка

Г. для уровней, энергия которых много меньше постоянной Планка 608. С помощью квазиклассиче-

ского правила квантования ^{U ( x )} ищутся энергии стационарных состояний в потенциале, график которого изображен на рисунке.

С 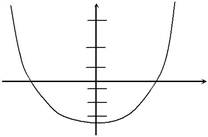помощью горизонтальных _x

отрезков на рисунке показаны энергии уровней, полученных из правила квантования. Для

какого из перечисленных уровней следует ожидать лучшего совпа-дения квазиклассического результата с точным?

А. для основного состояния Б. для второго уровня

В. для четвертого Г. для шестого

609. Какое из нижеследующих равенств является правилом кванто-вания Бора-Зоммерфельда

b					b
А. ∫		dx	πn	Б. ∫ k		(x) dx	πn
k		(x)
a				a
В. ∫ ^b k (x) dx πn	Г. ∫ ^b		dx πn
k (x)
a						a

где k (x) =	2 m E − U (x) /	^2, a и b – точки поворота
610.	Квазиклассическое	правило	квантования
∫ ^b k (x) dx = π (n +1/ 2)(где	k (x)=	2 m E − U (x) /	^2,	a и b –
a

классические точки поворота) является уравнением, из которого можно найти собственные значения оператора Гамильтона. В какие из нижеследующих величин входят искомые собственные значения (считать, что график зависимости потенциальной энергии не имеет «вертикальных» стенок)?

А. только в k (x)	Б. и в k (x), и в a, и в
В. b только в k (x) и a	Г. ни в одну из перечисленных
611.Уравнение Шредингера ре-	U (x)
шается в следующем потенциале:
U (x)=∞при x < a, U (x)–		E
некоторая плавная функция ко-
ординат при x > a (см. рисунок;			x
энергия E, для которой решается
уравнение также показана на ри-

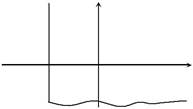сунке). Какой функцией определяется в области далекой от точки поворота при x > a хорошее квазиклассическое решение?

^x

^x

А.

cos

∫

k (t) dt

Б.

sin

∫

k (t) dt

k (x)

k (x)

a

a

x

^x

В.

exp i

∫

k (t) dt

Г.

sin

∫

k (t) dt

k (x)

k (x)

a

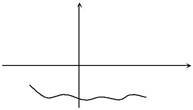
612.Каким будет правило кванто-

U (x)

вания в потенциале: U (x) = ∞ при

x < a и при x > b, U (x)

– неко-

торая

известная

плавная

функция

b x

координаты при

a < x < b

(беско-

нечно глубокая потенциальная яма

с «неплоским» дном; см. рисунок)?

А. ∫ ^b k (x) dx = πn	Б. ∫ ^b k (x) dx = π (n +1/ 4)
a	a
В. ∫ ^b k (x) dx = π (n +1/ 2)	Г. ∫ ^b k (x) dx = π (n +3/ 4),
a	a
где k (x) = 2 m (E − U (x))/	2 .

613. Чему равно значение параметра квазиклассичности при таких

значениях координаты, где	E = U (x)	(E – энергия, при которой
решается уравнение Шредингера в потенциале U (x))?
А. 0	Б. 1	В. ∞	Г. -1

ГЛАВА 7. ТЕОРИЯ ВОЗМУЩЕНИЙ

Дата добавления: 2014-12-24