Теория возмущений без вырождения 3 страница

А.	E	(1)	=	E ^2	Б.	E	(1)	= −	E ^2
	me ^2		me ^2
В.	E (1)	= 0	Г.	E (1)	=	2 E ^2
me ^2

659. На атом водорода накладывают малое возмущение^ˆ= α ². r

V

Какой формулой определяется поправка первого порядка к энергии основного состояния?

А.	E (1)	∼	α ^8	Б.	E (1)	∼		α ^6
	e			3 5
				m						m e
В.	E (1)	∼		α ^4	Г.	E (1)	∼	α ^2
	m ^2 e ^4		me ^2

660. Собственные значения ε_i и собственные функции ϕ_i некото-рой квантовой системы известны. Все собственные значения не

вырождены. На систему накладывается возмущение ^ˆ, матричные

V

элементы оператора которого с невозмущенными собственными функциями V_ik известны. Какой формулой определяется поправка

теории возмущений первого порядка к волновой функции энергии i -го стационарного состояния?

А.

^ϕ i

(1)

=

∑

^Vik

^ϕk

ε

− ε

k (k ≠ i)

i

k

(1)

∑

V

В.

ϕ i

=

ik

ϕk

ε

− ε

k (k ≠ i)

i

k

Б.

Г.

^ϕ i

(1)

=

∑

^Vik

^ϕk

k (k ≠ i)^( ε i − εk ^)

(1)

∑

V

ϕ i

=

ik

ϕk

k (k ≠ i)^( ε i − εk ^)

661. Будут ли волновые функции стационарных состояний ψ_i,вы-численные в первом порядке теории возмущений согласно формуле

ψi = ϕ i +∑			^Vik		ϕk,нормированы на единицу(здесь ϕi и εi
ε		− ε
k (k ≠ i)	i	k

– нормированные на единицу волновые функции и энергии невоз-мущенных состояний, V_ik – матричные элементы оператора воз-

мущения)? А. да, точно Б. нет

В. условие нормировки будет нарушаться во втором порядке по возмущению Г. условие нормировки будет нарушаться в первом порядке по воз-мущению

662. На осциллятор,находящийся в девяносто девятом стационар-ном состоянии (основное состояние – нулевое), накладывают малое

ˆ
возмущение V (x) = a sin(x / b). Как изменится средняя четность
этого состояния?
А. уменьшится	Б. увеличится	В. не изменится
Г. это зависит от частоты осциллятора	ˆ
			.
663.На осциллятор накладывают малое возмущение V (x)= αx

Как изменится средняя четность стационарных состояний осцилля-тора?

А. четных состояний – уменьшится, нечетных состояний – увели-чится Б. четных состояний – увеличится, нечетных состояний – умень-шится

В. для всех состояний – уменьшится Г. для всех состояний – увеличится (основное состояние – нулевое)

664. На осциллятор,находящийся в сотом стационарном состоянии(основное состояние – нулевое) накладывают малое возмущение

ˆ
V (x)= a cos(x / b).В первом порядке теории возмущений для вол-
новой функции найти среднюю четность этого состояния	a
А.			= −1		Б.		=1	В.		= − 1 +
P		P	P
ω
						a
Г.		= 1 −
P
	ω

665. На одномерный гармонический осциллятор наложили малое

возмущение ^ˆ = α. В первом порядке теории возмущений для

V (x) x

волновой функции найти вероятность того, что четность возму-щенного основного состояния осциллятора равна −1

А. w (P = −1) =	α ^2	Б. w (P = −1) =	α ^2
2 m ω ^3	4 m ω ^3
В. w (P = −1) =		α ^2	Г. w (P = −1) =	α ^2
	2 mω ^3		4 mω ^3

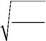
Указание. Матричный элемент оператора координаты с волновыми функциями основного ϕ ₀ (x) и первого возбужденного ϕ ₁(x) ста-

ционарных состояний гармонического осциллятора равен

∫ ^ϕ 0 ^{( x ) xϕ} 1 ^{( x ) dx =} _{2 m ω} ^.

666. На трехмерный гармонический осциллятор наложили малое

возмущение ^ˆ = α. Какие значения момента импульса

V (x, y, z) z

осциллятора и его проекции на ось z можно обнаружить в возму-щенном основном состоянии осциллятора? Ответ дать в первом порядке теории возмущений для волновой функции.

А. l = 0, 1; lz = 0	Б. l = 0;	lz =0, 1
В. l = 0, lz = 0	Г. l = 0, 1; lz = 0, 1, −1

667. На трехмерный гармонический осциллятор массой m и часто-

той ω накладывают малое возмущение ^ˆ =. Какие значения

V (r) ay

проекции момента импульса возмущенного осциллятора на ось z можно обнаружить в основном состоянии? Ответ дать в первом порядке теории возмущений для волновой функции.

А. lz = 0		Б. lz = 0, 1
В. lz = 0, −1	Г. lz = 0, ±1	ˆ
668.На атом водорода накладывают малое возмущение V = af (r),
где f (r)	– функция от модуля радиуса-вектора. Какие значения
момента импульса электрона и его проекции на ось z	можно обна-
ружить в возмущенном основном состоянии атома?
А. l = 0, 1, lz = 0, ±1	Б. l = 0, lz = 0
В. l = 0, 2, lz = 0, ± 2	Г. l = 0, 1, lz = 0
669.На	атом водорода	накладывают малое	возмущение
ˆ	= a cos ϑ. Какие значения момента импульса электрона и его
V

проекции на ось z можно обнаружить в основном состоянии ато-ма? Ответ дать в первом порядке теории возмущений для волновой функции.

А. l = 0, lz = 0	Б. l = 0, 1, lz = 0, ±1
В. l = 0, 2, lz = 0, ± 2	Г. l = 0, 1, lz = 0
670.На		атом водорода	накладывают малое возмущение
ˆ		ϕ. Какие значения проекции орбитального момента им-
V = a cos

пульса электрона на ось z можно обнаружить в возмущенном ос-новном состоянии атома? Ответ дать в первом порядке теории воз-мущений для волновой функции.

А. lz = 0				Б. lz = 0, ±1
В. lz = 0, ± 2			Г. lz = 0, ± 1, ± 2
671.	На атом	водорода	накладывают малое возмущение
ˆ	f (r) cos		ϑ,	где f (r) –	некоторая функция модуля радиус-
V =

вектора. Состояния с какими значениями момента импульса «при-мешиваются» к основному состоянию электрона в первом порядке теории возмущений? Ответ дать в первом порядке теории возму-щений для волновой функции.

А. l = 0			Б. l = 0, 1
В. l = 0, 1, 2	Г. l = 0, 2
672.На		атом	водорода накладывают малое возмущение
ˆ		ϑ. Какие значения проекции момента импульса элек-
V = a cos
трона на ось z	можно обнаружить в основном состоянии атома?

Ответ дать в первом порядке теории возмущений для волновой функции.

А. lz = 0	Б. lz = 0,	±1
В. lz = 0, ± 2	Г. lz = 0,	± 1, ± 2

673. На атом водорода накладывают малое возмущение,операторкоторого зависит только от z. Какие значения проекции момента импульса электрона на ось z можно обнаружить в основном со-стоянии атома? Ответ дать в первом порядке теории возмущений для волновой функции.

А. lz = 0	Б. lz = 0,	±1
В. lz = 0, ± 2	Г. lz = 0,	± 1, ± 2

Дата добавления: 2014-12-24