Перестановочная симметрия волновой функции систем тождественных частиц

828. Выберите правильное утверждениеА. фермионы – это частицы с четным спином Б. бозоны имеют полуцелый спин В. спин всех бозонов равен 2¹

Г. если частица имеет спин, равный 1/2, то это фермион 829. Выберите правильное утверждениеА. фермионы – это частицы с целым спином Б. бозоны – это частицы с нечетным спином

В. фермионы – это частицы с полуцелым спином Г. бозоны – это частицы с четным спином

830. Частица имеет спин s =3 / 4.Какое утверждение относитель-но свойств этой частицы справедливо?

А. эта частица – фермион Б. эта частица – бозон

В. эта частица – суперпозиция состояний бозона со спином s =1 и фермиона со спином s =1/ 2

Г. спин такого значения принимать не может 831. Волновая функция системы тождественных фермионов

А. симметрична относительно перестановок аргументов, относя-щихся к разным частицам Б. антисимметрична относительно перестановок аргументов, отно-сящихся к разным частицам

В. симметрична относительно замены r_i → − r_i

Г. антисимметрична относительно замены r_i → − r_i

832. Волновая функция системы тождественных бозоновА. симметрична относительно перестановок аргументов, относя-щихся к разным частицам

Б. антисимметрична относительно перестановок аргументов, отно-сящихся к разным частицам

¹ В этой главе =1.

В. симметрична относительно замены r_i → − r_i

Г. антисимметрична относительно замены r_i → − r_i

833. Что значит, что волновая функция двух тождественных бозо-нов симметрична относительно перестановок?

А. при перестановке значений, которые принимают пространствен-ные и спиновые координаты первой и второй частицы, функция не меняется Б. при перестановке значений, которые принимают только про-

странственные координаты первой и второй частицы, функция не меняется В. при перестановке значений, которые принимают только спино-

вые координаты первой и второй частицы, функция не меняется Г. является сферически симметричной

834. Что значит, что волновая функция двух тождественных фер-мионов антисимметрична относительно перестановок?

А. при перестановке значений, которые принимают пространствен-ные и спиновые координаты первой и второй частицы, функция меняет знак Б. при перестановке значений, которые принимают только про-

странственные координаты первой и второй частицы, функция ме-няет знак В. при перестановке значений, которые принимают только спино-

вые координаты первой и второй частицы, функция не меняется Г. является нечетной

835. Что такое определитель Слэттера?

А. это определитель секулярного уравнения Б. волновая функция тождественных бозонов

В. волновая функция тождественных фермионов Г. определитель матриц Паули

836. Какая из нижеследующих формул представляет собой опреде-литель Слэттера для системы двух тождественных невзаимодейст-вующих фермионов, один из которых находится в одночастичном

состоянии ϕ ₁, второй – в одночастичном состоянии ϕ ₂?

А.

ϕ 1(r 1) ϕ 1(r 2)

Б.

ϕ 1(r 1) ϕ 2(r 2)

ϕ 1(r 1)

ϕ 1(r 2)

ϕ 1(r 1)

ϕ 2(r 2)

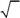
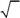
В.

ϕ 1(r 1) ϕ 1(r 2)

Г.

ϕ 2(r 1) ϕ 1(r 2)

ϕ 2(r 1)

ϕ 2(r 2)

ϕ 2(r 1)

ϕ 1(r 2)

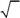
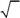
837. Имеется система тождественных невзаимодействующих фер-мионов со спином s = 99 / 2 каждый. Какое максимальное количе-ство частиц может находиться в одинаковом пространственном

состоянии?
А. 99	Б. 100	В. 101	Г. любое

838. Имеется система тождественных невзаимодействующих бозо-нов со спином s = 99 каждый. Какое максимальное количество частиц может находиться в одинаковом пространственном состоя-нии?

А. 99	Б. 100	В. 101	Г. любое
839.Может ли волновая функция
ψ (r 1, r 2)∼ ϕ 1(r 1) ϕ 2(r 2)+ ϕ 2(r 1) ϕ 1(r 2),
где ϕ 1 и ϕ 2	– функции одной переменной, описывать пространст-

венное состояние системы из двух тождественных фермионов со спином s =1/ 2 каждый?

А. да, поскольку эта функция симметрична относительно переста-новок Б. нет, поскольку эта функция симметрична относительно переста-новок

В. да, если спиновая часть волновой функции антисимметрична Г. это зависит от ϕ ₁, ϕ ₂ 840. Может ли волновая функция

,

ψ (r 1, r 2)∼(ϕ 1(r 1) ϕ 2(r 2)+ ϕ 2(r 1) ϕ 1(r 2))

−

где ϕ ₁ и ϕ ₂ – некоторые функции пространственной координаты, описывать состояние системы из двух тождественных фермионов со спином s =1/ 2 каждый?

А. да Б. нет В. зависит от ϕ ₁, ϕ ₂

Г. зависит от нормировочного множителя 841. Может ли волновая функция

ψ (r ₁, r ₂)∼ ϕ ₁(r ₁) ϕ ₂(r ₂)− ϕ ₂(r ₁) ϕ ₁(r ₂),

где ϕ ₁ и ϕ ₂ – некоторые функции пространственной координаты, описывать пространственное состояние системы из двух тождест-венных бозонов со спином s = 0 каждый?

А. да, поскольку эта функция антисимметрична относительно пере-становок Б. нет, поскольку эта функция антисимметрична относительно пе-

рестановок, а спиновой части эта функция не содержит В. да, если спиновая часть волновой функции антисимметрична

Г. это зависит от ϕ ₁, ϕ ₂ 842. Система тождественных бозонов имеет волновую функцию:

ψ ∼ ϕ _i (r ₁) ϕ _k (r ₂)+ ϕ _k (r ₁) ϕ_i (r ₂)+ ϕ_i (r ₁) ϕ _n (r ₂)+ ϕ _n (r ₁) ϕ_i (r ₂),

где i, k, n – квантовые числа одночастичных состояний. Сколько

частиц входят в систему? А. одна Б. две В. три

Г. эта система с неопределенным числом частиц

843. Два тождественных бозона со спином s =0каждый связаныпотенциалом, зависящим только от модуля относительного радиу-

са-вектора: U (r ₁, r ₂) = U (| r ₁ − r ₂ |). Какие значения может прини-мать орбитальный момент относительного движения?

А. только l = 0 Б. только l =1

В. только четные значения Г. только нечетные значения

844. Система из трех тождественных бозонов со спином s =0ка-ждый находится в состоянии, в котором две частицы находятся в одночастичном состоянии i, одна – в одночастичном состоянии k.

Какой формулой определяется волновая функция системы (ϕ_i (r) и ϕ_k (r)–одночастичные волновые функции)?

А. Ψ (r ₁, r ₂, r ₃) = ϕ _i (r ₁) ϕ _i (r ₂) ϕ_k (r ₃)

Б. Ψ (r ₁, r ₂, r ₃) = ¹₂ (ϕ _i (r ₁) ϕ _i (r ₂) ϕ _k (r ₃) + ϕ _i (r ₁) ϕ _i (r ₃) ϕ_k (r ₂))

_В. Ψ (r ₁, r ₂, r ₃) = ¹₃ (ϕ _i (r ₁) ϕ _i (r ₂) ϕ_k (r ₃) +

+ ϕ _i (r ₁) ϕ _i (r ₃) ϕ _k (r ₂) + ϕ _i (r ₃) ϕ _i (r ₂) ϕ_k (r ₁))

Г. такого состояния в системе бозонов быть не может 845. Три тождественных невзаимодействующих фермиона со спи-

ном s =1/ 2 каждый движутся в некотором потенциале. Собствен-ные функции одночастичного гамильтониана ϕ_i (x) известны

(x = r, σ_z индекс i включает в себя и «спиновые» квантовые чис-

ла). Какой формулой определяется волновая функция состояния системы частиц, в котором два фермиона находятся в одночастич-ном состоянии i, один – в одночастичном состоянии k?

А. Ψ (x ₁, x ₂, x ₃) = ϕ _i (x ₁) ϕ _i (x ₂) ϕ_k (x ₃)

Б. Ψ (x ₁, x ₂, x ₃) = ¹₂ (ϕ _i (x ₁) ϕ _i (x ₂) ϕ _k (x ₃) − ϕ _i (x ₁) ϕ _i (x ₃) ϕ_k (x ₂))

_В. Ψ (x ₁, x ₂, x ₃) = ¹₃ (ϕ _i (x ₁) ϕ _i (x ₂) ϕ_k (x ₃) −

− ϕ _i (x ₁) ϕ _i (x ₃) ϕ _k (x ₂) − ϕ _i (x ₃) ϕ _i (x ₂) ϕ_k (x ₁)

Г. такого состояния в системе фермионов быть не может 846. Гамильтониан системы тождественных фермионов

А. симметричен относительно перестановок координат частиц, так как это фермионы Б. антисимметричен относительно перестановок координат, так это фермионы

В. симметричен относительно перестановок координат частиц, так как частицы тождественные Г. антисимметричен относительно перестановок координат частиц, так как частицы тождественные

847. Гамильтониан системы тождественных бозоновА. симметричен относительно перестановок координат частиц, так как это бозоны

Б. антисимметричен относительно перестановок координат, так это бозоны В. симметричен относительно перестановок координат частиц, так

как частицы тождественные

Г. антисимметричен относительно перестановок координат частиц, так как частицы тождественные

848. Гамильтониан системы тождественных невзаимодействующих частиц А. равен сумме одинаковых операторов, каждый из которых дейст-

вует на координаты только одной частицы Б. равен произведению одинаковых операторов, каждый из кото-

рых действует на координаты только одной частицы В. равен сумме одинаковых операторов, каждый из которых дейст-вует на координаты только одной пары частиц

Г. равен произведению одинаковых операторов, каждый из кото-рых действует на координаты только одной пары частиц

849. Два тождественных невзаимодействующих бозона со спином

s =0каждый находятся в потенциале одномерного гармоническо-го осциллятора. Какова кратность вырождения второго возбужден-

ного уровня энергии системы?
А. 1	Б. 2	В. 3	Г. 4

850. Десять тождественных невзаимодействующих фермионов соспином s =1/ 2 находятся в потенциале одномерного гармониче-ского осциллятора с частотой ω. Какова энергия основного со-стояния системы?

А. 24 ω Б. 25 ω В. 26 ω Г. 27 ω

851. Десять тождественных невзаимодействующих фермионов соспином s = 3 / 2 находятся в потенциале одномерного гармониче-ского осциллятора с частотой ω. Какова энергия основного со-стояния системы?

А. 10 ω Б. 11 ω В. 12 ω Г. 13 ω

852. Десять тождественных невзаимодействующих бозонов со спи-ном s =1 находятся в потенциале одномерного гармонического осциллятора с частотой ω. Какова энергия основного состояния системы?

А. 5 ω Б. 6 ω В. 7 ω Г. 8 ω 853. Два тождественных невзаимодействующих фермиона со спи-

ном s =1/ 2 каждый находятся в потенциале одномерного гармо-нического осциллятора. Какова кратность вырождения второго возбужденного уровня энергии системы?

А. 3 Б. 4 В. 5 Г. 6

854. Два тождественных невзаимодействующих бозона со спином s =0каждый находятся в потенциале сферического осциллятора.Какова кратность вырождения второго возбужденного уровня энергии системы?

Указание: кратности вырождения уровней энергии трехмерного осциллятора равны: 1 – для основного состояния, 3 – для первого возбужденного, 6 – для второго возбужденного.

А. 10 Б. 12 В. 14 Г. 16

855. Имеются два фермиона со спином s =1/ 2каждый.Что мож-но сказать о спиновой волновой функции состояния с определен-ным суммарным спином S =1?

А. эта функция антисимметрична относительно перестановок спи-новых координат частиц, так как частицы – фермионы Б. эта функция не обладает определенной симметрией по отноше-нию к перестановкам спиновых координат

В. эта функция антисимметрична относительно перестановок спи-новых координат частиц по построению независимо от того, явля-ются частицы тождественными или нет Г. эта функция симметрична относительно перестановок спиновых

координат частиц по построению независимо от того, являются частицы тождественными или нет

856. Имеются два фермиона со спином s =1/ 2каждый.Что мож-но сказать о спиновой волновой функции состояния с определен-ным суммарным спином S = 0?

А. эта функция антисимметрична относительно перестановок спи-новых координат частиц, так как частицы – фермионы Б. эта функция не обладает определенной симметрией по отноше-нию к перестановкам спиновых координат

В. эта функция антисимметрична относительно перестановок спи-новых координат частиц по построению независимо от того, явля-ются частицы тождественными или нет Г. эта функция симметрична относительно перестановок спиновых

координат частиц по построению независимо от того, являются частицы тождественными или нет

857. Имеются два фермиона со спином s =1/ 2каждый.Какое ут-верждение относительно спиновой функции состояния, в котором проекция суммарного спина на ось z имеет определенное значение

S_z =0,а сам суммарный спин определенного значения не имеет,

является верным?

А. эта функция антисимметрична относительно перестановок спи-новых координат частиц, так как частицы – фермионы Б. эта функция, вообще говоря, не обладает определенной симмет-рией по отношению к перестановкам спиновых координат

В. эта функция антисимметрична относительно перестановок спи-новых координат частиц по построению независимо от того, явля-ются частицы тождественными или нет Г. эта функция симметрична относительно перестановок спиновых

координат частиц по построению независимо от того, являются частицы тождественными или нет

858. Имеются два фермиона со спином s =99 / 2каждый.Чтоможно сказать о симметрии спиновой волновой функции состоя-ния, в котором суммарный спин имеет определенное значение

S =97?

А. эта функция антисимметрична относительно перестановок спи-новых координат частиц, так как частицы – фермионы Б. эта функция не обладает определенной симметрией по отноше-нию к перестановкам спиновых координат

В. эта функция антисимметрична относительно перестановок спи-новых координат частиц по построению независимо от того, явля-ются частицы тождественными или нет Г. эта функция симметрична относительно перестановок спиновых

координат частиц по построению независимо от того, являются частицы тождественными или нет

859. Имеются два бозона со спином s каждый.Что можно сказатьо спиновой волновой функции состояния, в котором суммарный спин имеет определенное значение S = 2 s?

А. эта функция симметрична относительно перестановок спиновых координат частиц, так как частицы – бозоны Б. эта функция не обладает определенной симметрией по отноше-нию к перестановкам спиновых координат

В. эта функция антисимметрична относительно перестановок коор-динат частиц по построению независимо от того, являются частицы тождественными или нет

Г. эта функция симметрична относительно перестановок координат частиц по построению независимо от того, являются частицы тож-дественными или нет

860. Имеются два бозона со спином s каждый.Что можно сказатьо спиновой волновой функции состояния, в котором суммарный спин имеет определенное значение S = 2 s −1?

А. эта функция симметрична относительно перестановок спиновых координат частиц, так как частицы – бозоны Б. эта функция не обладает определенной симметрией по отноше-нию к перестановкам спиновых координат

В. эта функция антисимметрична относительно перестановок коор-динат частиц по построению независимо от того, являются частицы тождественными или нет Г. эта функция симметрична относительно перестановок координат

частиц по построению независимо от того, являются частицы тож-дественными или нет

861. Два тождественных фермиона со спином s =3 / 2каждый на-ходятся в состоянии с определенным суммарным спином S. Будет ли пространственная часть волновой функции системы обладать определенной симметрией по отношению к перестановкам?

А. да	Б. нет	В. будет, если S = 3 или S =1
Г. будет, если S = 2 или S = 0
862.Система из двух тождественных	фермионов	со спином
s =1/ 2	каждый находится в	состоянии,	в котором	суммарный

спин не имеет определенного значения. Будет ли пространственная часть волновой функции системы обладать определенной симмет-рией по отношению к перестановкам?

А. да	Б. нет	В. это зависит от состояния
Г. это зависит от проекции суммарного спина
863.Система из двух	тождественных	фермионов	со спином
s =1/ 2	каждый находится в состоянии,	в котором	суммарный

спин имеет определенное значение S =1. Какова вероятность того, что частицы окажутся в одной точке пространства?

А. w = 0	Б. w =1/ 4	В. w =1/ 3	Г. w =1/ 2
864.Система из	двух	тождественных	фермионов со спином
s =1/ 2	находится	в состоянии с пространственной волновой

функцией ψ (r ₁, r ₂) ∼ ϕ ₁ (r ₁) ϕ ₂ (r ₂) + ϕ ₂ (r ₁) ϕ ₁ (r ₂). Имеет ли суммар-ный спин системы определенное значение в этом состоянии, и если да, то какое?

А. да, S =1	Б. нет	В. да,	S =0
В. зависит от состояния
865.Система из	двух тождественных	фермионов со	спином
s =1/ 2находится	в состоянии с пространственной волновой

функцией ψ (r ₁, r ₂) ∼ ϕ ₁ (r ₁) ϕ ₂ (r ₂) − ϕ ₂ (r ₁) ϕ ₁ (r ₂). Имеет ли проекция

суммарного спина системы на ось z	определенное значение в этом
состоянии, и если да, то какое?
А. да, Sz =1	Б. нет	В. да, Sz = 0
Г. это зависит от состояния

866. Система из двух тождественных невзаимодействующих бозо-нов со спином s =1 находится в состоянии, в котором пространст-венная часть волновой функции симметрична относительно пере-становок координат. Имеет ли суммарный спин такой системы оп-

ределенное значение?

А. да Б. нет В. вообще говоря, нет

Г. это зависит от пространственного состояния 867. Система из двух тождественных невзаимодействующих бозо-

нов со спином s =1 находится в состоянии, в котором пространст-венная часть волновой функции антисимметрична относительно перестановок координат. Имеет ли суммарный спин такой системы определенное значение?

А. да Б. нет В. вообще говоря, нет Г. это зависит от пространственного состояния 868. Два тождественных невзаимодействующих бозона со спином

s =2находятся в одинаковых пространственных состояниях.Ка-кие значения суммарного спина системы можно обнаружить при измерениях?

А. только S = 4

Б. только S = 2

В. только S = 0, S = 2 и S = 4

Г. все возможные значения S = 0, S =1, S = 2, S = 3 и S = 4 869. Два тождественных невзаимодействующих фермиона со спи-ном s = 3 / 2 находятся в одинаковых пространственных состояни-

ях. Какие значения суммарного спина системы можно обнаружить при измерениях?

А. S = 3 и S =1

Б. только S = 2

В. S = 2 и S = 0

Г. все возможные значения S = 0, S =1, S = 2, S = 3

870. Известно,что волновая функция системы двух тождественныхчастиц, описывающая состояние с определенным суммарным спи-ном S = 0, является симметричной относительно перестановок пространственных координат частиц. Какие это частицы?

А. фермионы Б. бозоны

В. информации недостаточно Г. это зависит от пространственного состояния

Дата добавления: 2014-12-24